2019 GDUT Rating Contest I : Problem B. Teamwork

题面：

传送门

B. Teamwork

Input file: standard input

Output file: standard output

Time limit: 1 second

Memory limit: 256 megabytes

 

For his favorite holiday, Farmer John wants to send presents to his friends. Since he isn’t very good at wrapping presents, he wants to enlist the help of his cows. As you might expect, cows are not much better at wrapping presents themselves, a lesson Farmer John is about to learn the hard way. Farmer John’s N cows (1 ≤ N ≤ 10^4) are all standing in a row, conveniently numbered 1...N in order. Cow i has skill level si at wrapping presents. These skill levels might vary quite a bit, so FJ decides to combine his cows into teams. A team can consist of any consecutive set of up to K cows (1 ≤ K ≤ 10^3), and no cow can be part of more than one team. Since cows learn from each-other, the skill level of each cow on a team can be replaced by the skill level of the most-skilled cow on that team. Please help FJ determine the highest possible sum of skill levels he can achieve by optimally forming teams.

 

Input

The first line of input contains N and K. The next N lines contain the skill levels of the N cows in the order in which they are standing. Each skill level is a positive integer at most 105.

 

Output

Please print the highest possible sum of skill levels FJ can achieve by grouping appropriate consecutive sets of cows into teams.

 

Example

Input

7 3
1
15
7
9
2
5
10

Output

84

 

Note

In this example, the optimal solution is to group the first three cows and the last three cows, leaving the middle cow on a team by itself (remember that it is fine to have teams of size less than K). This effectively boosts the skill levels of the 7 cows to 15, 15, 15, 9, 10, 10, 10, which sums to 84.

 

题目描述：

有n头奶牛，我们可以让连续的奶牛组成一队，组队后队里所有奶牛的等级就会变成队里等级最高的那个，求n头奶牛经过组队后，所有奶牛的等级之和最大的是多少。一队奶牛的数量最多不超过C头牛。

 

题目分析：

这道题可以用动态规划解决：我们先重新定义这个问题：求前n头牛的等级之和最大值是多少？再看看这个问题的子问题：前i头牛的等级之和最大值是多少？（1 <= i <= n）会想到如何联系子问题和我们要求的题目问的问题，其实就是：我已经知道前i头牛的等级之和最大值是多少，然后通过这个计算出前n头牛的等级之和最大值是多少。然后，我们可以定义一个dp[i]数组来记录前i头牛的等级之和最大值，来通过利用dp[i]的值算出dp[n]。

 

我们具体看看样例怎样算：首先，我们已经知道dp[i]（1 <= i <= 6）的值，求dp[7]。我们对最后一头牛，也就是第7头牛进行分类讨论：

 

1.第7头奶牛自己组成一队，那么，dp[7] = dp[6] + 10

 

 

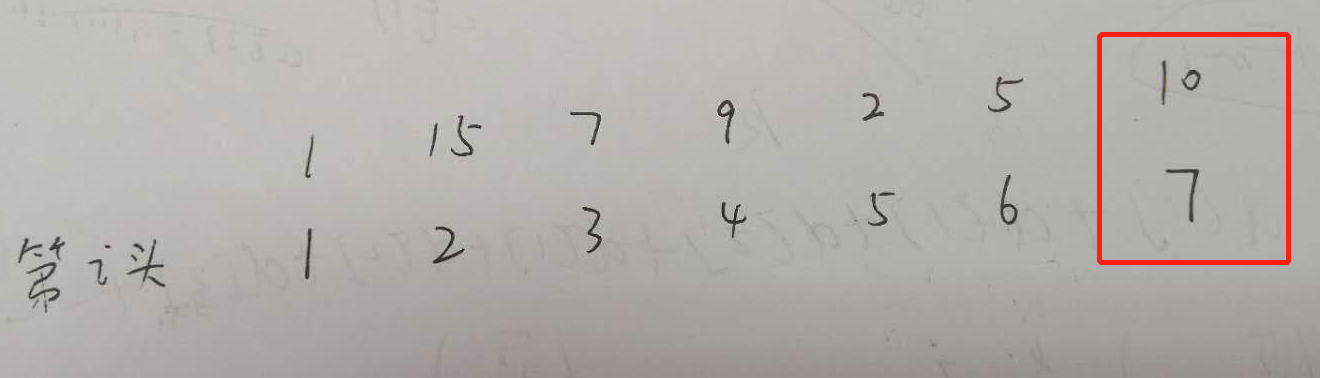
2.第7头奶牛和前面的一头奶牛组成一队，那么，dp[7] = dp[5] + 10 * 2

 

 

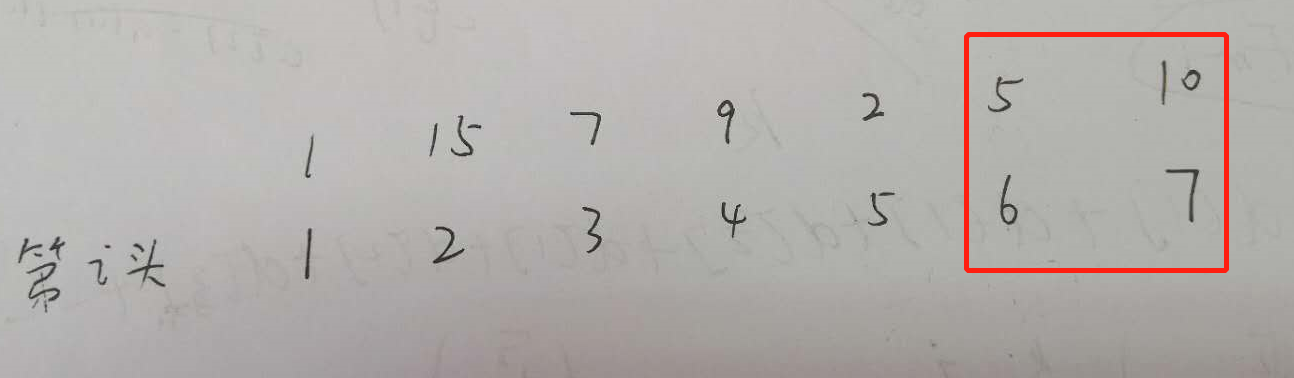
3.第7头奶牛和前面的两头奶牛组成一队，那么，dp[7] = dp[4] + 10 * 3

然后选出最大的那种情况就可以了。

那么，dp[4]， dp[5]， dp[6]怎么求？我们可以用求dp[7]的方法同样求出这三个的值。

状态转移方程：dp[i] = max{ dp[i-j] + j * max level[k] ( i-j+1 <= k <= i ) }   

 

 

AC代码：

 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 1e4+5;
const int maxk = 1e3+5;
int n, k;
int a[maxn];
int dp[maxn];

void test(){
    cout << endl;
    for(int i = 1; i <= n; i++){
        printf("dp[%d] = %d
", i, dp[i]);
    }
}

int main(){
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);


    for(int i = 1; i <= n; i++){
        int pre_max = 0;
        for(int j = 1; j <= k; j++){
            if(i >= j){
                if(a[i-j+1] > pre_max) pre_max = a[i-j+1];
                dp[i] = max(dp[i], dp[i-j]+pre_max*j);
            }
        }
    }

    //test();
    printf("%d
", dp[n]);
    return 0;
}