树的定义:树( t r e e) t 是一个非空的有限元素的集合,其中一个元素为根( r o o t),余下的元素(如果有的话)组成 t 的子树( s u b t r e e)。
树中层次最高的元素为根,其下一集的元素是余下元素所构成子树的根。
树的另一常用术语为级(level)。指定树根的级为1。
元素的度(degree of an element)是指其孩子的个数。叶节点的度为0.树的度是其元素度的最大值。
二叉树的定义:二叉树( binary tree) t 是有限个元素的集合(可以为空) 。当二叉树非空时,
其中有一个称为根的元素,余下的元素(如果有的话)被组成 2个二叉树,分别称为 t的左子树
和右子树。
二叉树和树的根本区别是:
• 二叉树可以为空,但树不能为空。
• 二叉树中每个元素都恰好有两棵子树(其中一个或两个可能为空)。而树中每个元素可有
若干子树。
• 在二叉树中每个元素的子树都是有序的,也就是说,可以用左、右子树来区别。而树的
子树间是无序的。
二叉树的特性:
特性1 :包含n个元素的二叉树边数为n-1
证明 二叉树中每个元素 (除了根节点 ) 有且只有一个父节点。在子节点与父节点间有且只有一
条边,因此边数为n- 1。
特性2:若二叉树的高度为h,h>=0,则该二叉树最少有h个元素,最多有2h-1个元素。
特性3:包含n个元素的二叉树的高度最大为n,最小为log2(n+1) (向上取整)
满二叉树(除叶节点外,每个节点都有左右2个子节点),完全二叉树(除最后一层外,每层都满)
完全二叉树中元素与孩子编号的关系:
特性4:设完全二叉树中一元素的序号为i,1<=i<=n.则有以下关系:
当i=1时,节点为树的根。若i>1,则该元素父节点为i/2(向下取整)
当2*i>n时,该元素无左孩子。否则,其左孩子为2*i。
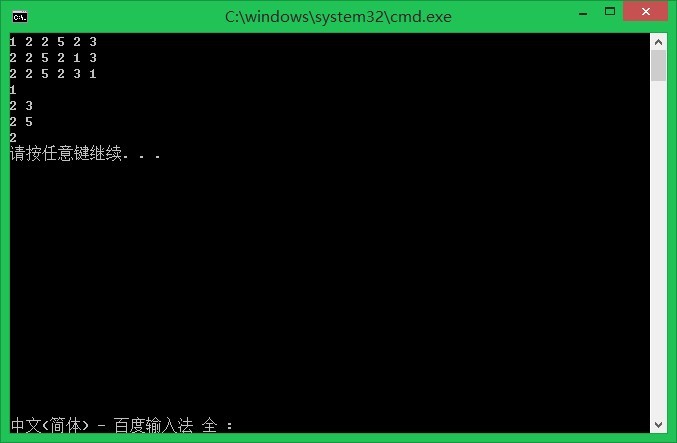
当2*i+1>n时,无右孩子。否则,右孩子为2*i+1。二叉树的公式化描述:二叉树的公式化描述利用了特性 4。二叉树可以作为缺少了部分元素的完全二叉树。图 8 - 8给出二叉树的两个样例。第一棵二叉树有三个元素 ( A、 B和C ),第二棵二叉树有五个元素 ( A、B、 C、 D和E )。没有涂阴影的圈表示缺少的元素。所有的元素 (包括缺少的元素 )按前面介绍的方法编号。在公式化描述方法中,按照二叉树对元素的编号方法,将二叉树的元素存储在数组中。图8 - 8同时给出了二叉树的公式化描述。缺少的元素由白圈和方格描述。当缺少很多元素时,这种描述方法非常浪费空间。实际上,一个有 n 个元素的二叉树可能最多需要 2n- 1 个空间来存储。当每个节点都是其他节点的右孩子时,存储空间达到最大。图 8 - 9给出这种情况下一棵有四个元素的二叉树,这种类型的二叉树称为右斜 ( r i g h t - s k e w e d )二叉树。当缺少的元素数目比较少时,这种描述方法很有效。
遍历方式:
前序遍历:先左子树,后根节点,后右子树
中序遍历:先根后左最后右
后序遍历:先左后右最后根
层级遍历:按层级遍历
C++代码实现:
类定义:
1 #ifndef BINARYTREEARRAY_H 2 #define BINARYTREEARRAY_H 3 #include <iostream> 4 5 template<class T> 6 class arrayTree 7 { 8 public: 9 arrayTree(T *t, int end) :data(t), Last(end){ } 10 void preOrder(int i);//前序 11 void inOrder(int i);//中序 12 void postOrder(int i);//后序 13 void levelOrder();//层级 14 int getLeftChildPos(int i){ return (2 * i) > Last ? -1 : 2 * i; } 15 int getRightChildPos(int i){ return (2 * i + 1) > Last ? -1 : 2 * i + 1; } 16 private: 17 T* data; 18 int Last; 19 }; 20 21 template<class T> 22 void arrayTree<T>::preOrder(int i) 23 { 24 if(Last==0) 25 { 26 std::cout << "empty tree" << std::endl; 27 return; 28 } 29 if(i<=Last) 30 { 31 if (data[i-1] != 0) 32 { 33 std::cout << data[i-1] << " "; 34 } 35 if (getLeftChildPos(i) != -1) 36 preOrder(getLeftChildPos(i)); 37 if (getRightChildPos(i) != -1) 38 preOrder(getRightChildPos(i)); 39 } 40 } 41 42 template<class T> 43 void arrayTree<T>::inOrder(int i) 44 { 45 if(Last==0) 46 { 47 std::cout << "empty tree" << std::endl; 48 return; 49 } 50 if(i<=Last) 51 { 52 if(data[i-1]!=0) 53 { 54 if (getLeftChildPos(i) != -1) 55 inOrder(getLeftChildPos(i)); 56 57 std::cout << data[i - 1] << " "; 58 59 if (getRightChildPos(i) != -1) 60 inOrder(getRightChildPos(i)); 61 } 62 } 63 } 64 65 template<class T> 66 void arrayTree<T>::postOrder(int i) 67 { 68 if(Last==0) 69 { 70 std::cout << "empty tree" << std::endl; 71 } 72 if(i<=Last) 73 { 74 if(data[i-1]!=0) 75 { 76 if (getLeftChildPos(i) != -1) 77 postOrder(getLeftChildPos(i)); 78 if (getRightChildPos(i) != -1) 79 postOrder(getRightChildPos(i)); 80 81 std::cout << data[i - 1] << " "; 82 } 83 } 84 } 85 86 template<class T> 87 void arrayTree<T>::levelOrder() 88 { 89 int level = 1; 90 int i = 1; 91 while (i<=Last) 92 { 93 for (int j = 0; j < (1 << (level-1))&&i<=Last;++j,++i) 94 { 95 if (data[i-1]!=0) 96 { 97 std::cout << data[i - 1] << " "; 98 } 99 } 100 std::cout<<std::endl; 101 level++; 102 } 103 } 104 #endif // !BINARYTREEARRAY_H
测试代码:
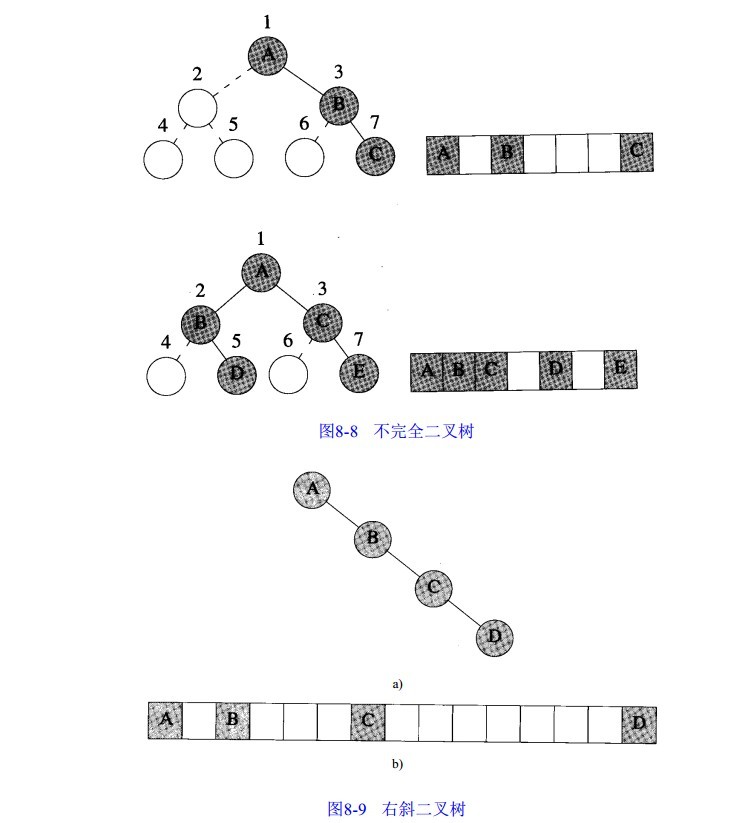
1 #include "binaryTreeArray.h" 2 3 int main() 4 { 5 int a[] = { 1, 2, 3, 2, 5, 0, 0, 0, 0, 0,2, 0, 0, 0 };//0表示虚节点 6 7 arrayTree<int> tree(a, 11); 8 tree.preOrder(1); 9 std::cout << std::endl; 10 tree.inOrder(1); 11 std::cout << std::endl; 12 tree.postOrder(1); 13 14 std::cout << std::endl; 15 tree.levelOrder(); 16 system("pause"); 17 18 return 0; 19 }
输出结果: