试题内容来自https://www.cnblogs.com/fyunaru/archive/2019/07/02/11123804.html
本文基于该试题添加了解析,仅供参考
一、判断题(10 * 2 分)
1.A*算法一定可以得到最优解。正确
A*算法定义:
(1)使用最佳优先策略搜索
(2)节点n的代价函数:f(n)=g(n)+h(n),g(n)是起点到节点n的最短路径代价,h(n)是节点n到目标节点的估计代价
(3)h(n)<=h*(n),h(n)表示节点n到终点的估计代价,h*(n)表示节点n到终点的实际代价(保证A*算法一定得到最优解的条件)
(4)当选择到的节点是目标节点时,算法停止,返回一个最优解
A*算法代价函数估计公式:f(n)=g(n)+h(n)
g(n)=0时,仅计算任意节点n到目标节点的启发函数,而不计算节点到节点n的最短距离,算法转化为使用贪心策略的最佳优先搜索,速度最快,但可能找不到最优解;
h(n)<=h*(n)时,一定可以求出最优解,h(n)越小,需要计算的节点越多,算法效率越低,常见的启发函数有曼哈顿距离、欧几里得距离等
h(n)=0时,仅计算起点到任意节点n的最短距离,而不计算任何启发函数h(n),转化为单源最短路径问题,即Dijkstra算法,需要计算最多的节点
2.调试程序可以证明算法的正确性。错误
算法的正确性定义:对于每一个输入都最终停止,而且产生正确的输出
算法的正确性证明:(1)证明算法对所有输入都终止(2)证明对每个输入都产生正确结果
程序调试!=程序正确性证明:程序调试只能证明程序有错,不能证明程序无错误
循环不变量方法:证明主要结构是循环结构的算法的正确性
3.dijkstra算法是贪心算法。
算法维护两个顶点集合S和Q。集合S保留所有已知实际最短路径值的顶点,而集合Q则保留其他所有顶点。
集合S初始状态为空,而后每一步都有一个顶点从Q移动到S。这个被选择的顶点是Q中拥有最小的d[u]值的顶点。
当一个顶点u从Q中转移到了S中,算法对u的每条外接边w(u,v)进行松弛。
4.如果一个基于比较的排序算法的时间复杂性是Ω(nlogn),那么他可能是基于比较算法中时间复杂性最低的算法。正确
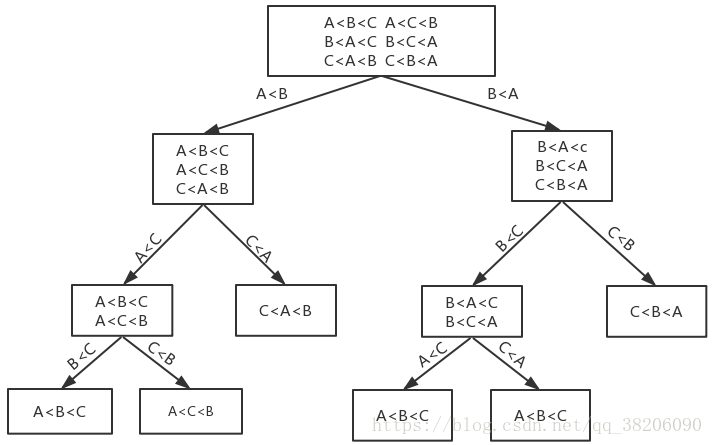
假设需要排序的数有N个,N个数有N!种不同的排序情况,即基于比较的排序算法的判定树有N!个叶子节点。
比较次数最少为log(N!)=O(NlogN)
5.一个关于堆排序的插入和删除操作的时间复杂性的问题。(具体怎么问忘了)
原地堆排序:
(1)创建一个堆H[0:n]
(2)把堆首与堆尾互换
(3)把堆的尺寸减1,并调用堆调整,将新的堆顶端元素调到合适位置
(4)不断重复(2)(3)两个步骤,直到堆的尺寸为1
堆的插入操作:将新元素插入堆尾,已知新元素的父节点到根节点是一个有序的序列,将新元素插入到该序列中,可以视为直接插入排序。(时间复杂度O(logn))
堆的删除操作:将堆顶元素与堆尾元素调换位置;堆尺寸减1,对新堆进行堆调整。(时间复杂度O(logn))
6.一个问KMP算法的时间复杂性的问题。
KMP算法可在一个主文本字符串S内查找一个词W(或称模式串)的出现位置
如果文本串的长度为 n,模式串的长度为 m,那么匹配过程的时间复杂度为 O(n),算上计算 next 的 O(m) 时间,KMP 的整体时间复杂度为 O(m + n)
二、简答题(5 * 4分)
1.一个master定理的题目(很类似于ppt上的一道例题)应该是T(n) = 3T(n/4) + n^(1/2)
https://zh.wikipedia.org/wiki/%E4%B8%BB%E5%AE%9A%E7%90%86
a=3,b=4
f(n)=n^(1/2) = O(n^(log_4(3-1))),符合情形一的情况
T(n)=Theta(n^(log_4(3)))
2.一个非常简单的复杂函数阶的证明,已知fx = O(g(x)), gx = o(hx),证明 fx = o(hx)
证明:
f(x)=O(g(x)) => 对于任意的c1,c2>0,x > x0时,c1*g(x) <= f(x) <= c2*g(x)
g(x)=o(h(x)) => 对于任意的c>0,x > x1时,g(x) < c*h(x)
当x>max(x0,x1)时,f(x) <= c2*g(x) => f(x) < c2*c*h(x) = C*h(x),其中C=c2*c
因此f(x) = o(h(x))
3.写出0-1背包问题的输入规模和时间复杂性
输入:C>0, w_i>0, v_i>0, 1<=i<=n
输出:(x_1,x_2,...,x_n), x_i in {0, 1},满足sum_{1=<i<=n}w_i*x_i<=C},
输入规模:一个问题的输入规模是保存输入数据所需要的bit位数。
输入规模:x = logC
动态规划解法:设dp[i][j]代表从0-i中挑选一些整数,每个物品只能使用一次,是否能够恰好填满容量为j的背包
for i = 1 to n:
for j = 0 to C:
dp[i][j] = dp[i - 1][j]
if nums[i] == j:
dp[i][j]=True
continue
if nums[i] < j:
dp[i][j]=dp[i-1][j] or dp[i-1][j-nums[i]]
标准多项式时间复杂度:对于一个问题,在输入规模为x的情况下,如果一个算法能够在O(x^k)时间内解决此问题,则我们称此算法是多项式时间的,其中k为一常数。
动态规划解法时间复杂度:O(nC) = O(n*(2^x))
传统时间复杂度与标准时间复杂度对比
相似:图论、链表、数组、树等问题
不同:数论问题(例如素数判定算法,传统时间复杂度O(n),输入规模x=logn,标准时间复杂度O(2^x))
若一个算法的传统时间复杂度为多项式的,但标准时间复杂度不是多项式的,则算法为伪多项式时间复杂度算法
4.说明平摊分析的目的,以及任举一种平摊分析方法说明其大致思想,以及使用时需要注意的点
三、(8分)
一个最大流的问题,给了一个最大流的图‘
第一问要求画出某一步之后的余图
第二问要求找出一条可以使流量增加1的増广路径
第三问要求给出一个最小割
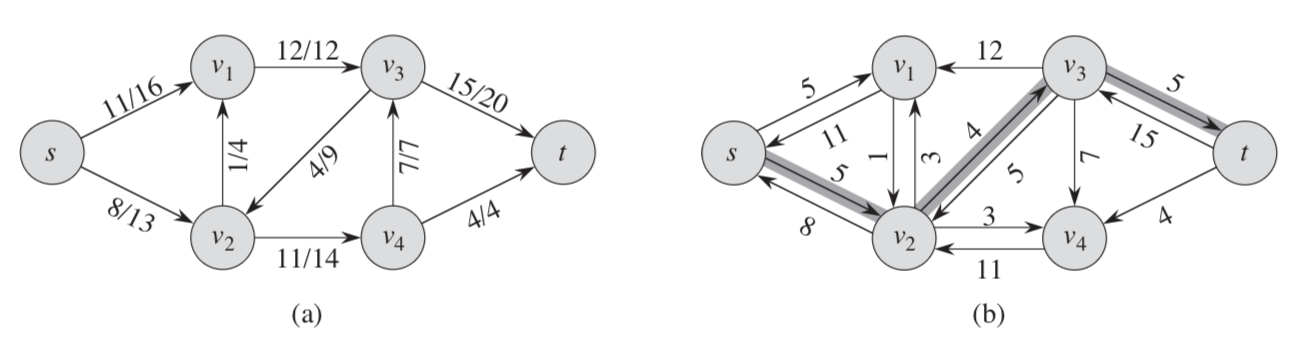
图(a)为一个流网络,图(b)展示了它的余图
符号定义:flow(a)代表边a的流量,c(a)代表边a的容量,s-t路径是指从起点s通往目标点t的任意一条路径
余图:余图(residual graph)的顶点和原图一样,如上图右所示,它包含两类弧:(1)原图的未饱和弧;(2)原图flow(a)>0的弧的反向弧。
增广路径:一条满足flow(a)<c(a)弧构成的s-t路径,上图(b)中s-v2-v3-t,容量为4的路径即为增广路径
流网络的割:流网络G中的一个割(S, T)将结点集合V划分为S和T=V-S两个集合,满足s in S,t in T
推论:流与割的弱对偶关系
给定流网络 G=(V,E),s是源,t是汇. 设f是G上的一个流,S,T是G的任意一个割,则f(S,T)=|f|.
给定流网络 G=(V,E). 设f是G上的一个流,(S,T)是G的任意一个割,则|f| <= c(S,T)
最小割:任意流不大于任意割,最大流等于最小割。
最大流算法(Ford-Fulkerson算法):
(1)建立原图流为0的余图;
(2)在余图中找出任意的s-t路径,并按该路径找出原图允许的最大流K:
- 最大流K根据弧的容量减去已有的流;
- 对余图的正向弧,原图的流加上K;
- 对余图的反向弧,原图的流减去K。
(3)更新余图,重复上述过程,直到余图不存在s-t路径。
5分钟看懂Ford-Fulkerson算法:https://www.youtube.com/watch?v=Tl90tNtKvxs
四、(7分)
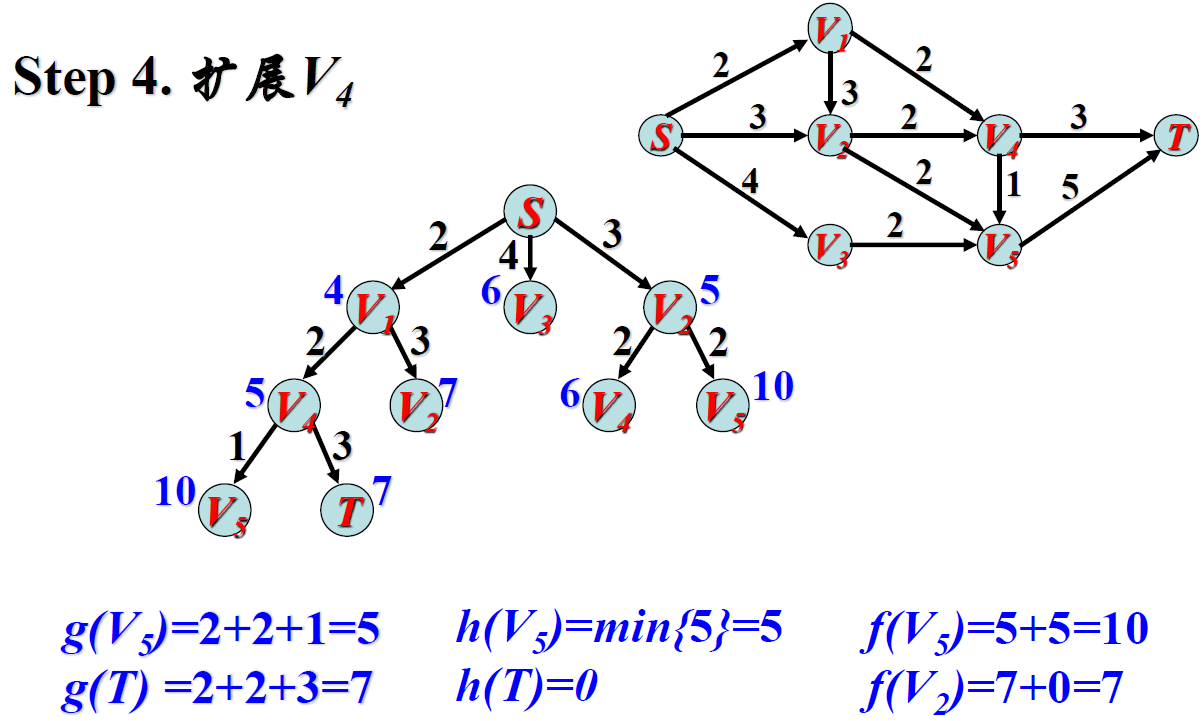
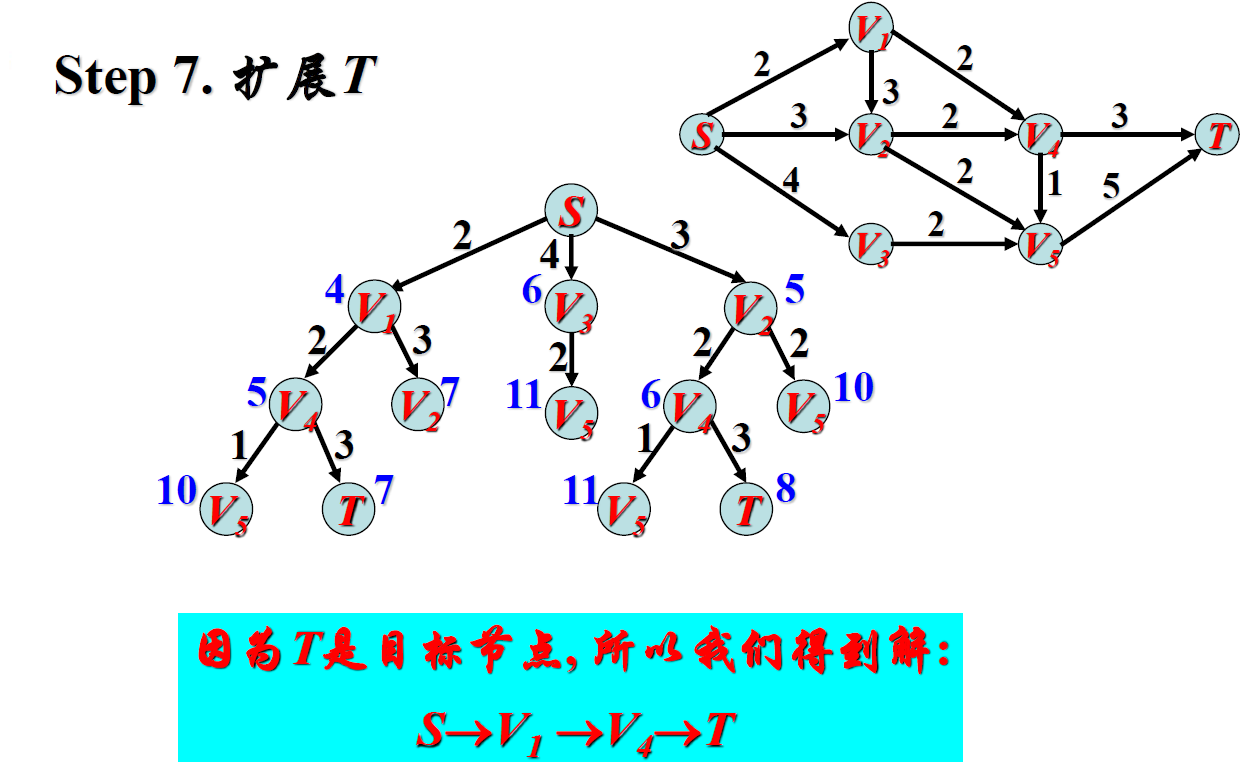
给出一个加权有向图,要求用A*算法把整个过程写一遍,并给出最后所得的最短路径。
A*算法的通俗介绍(https://www.redblobgames.com/pathfinding/a-star/introduction.html)
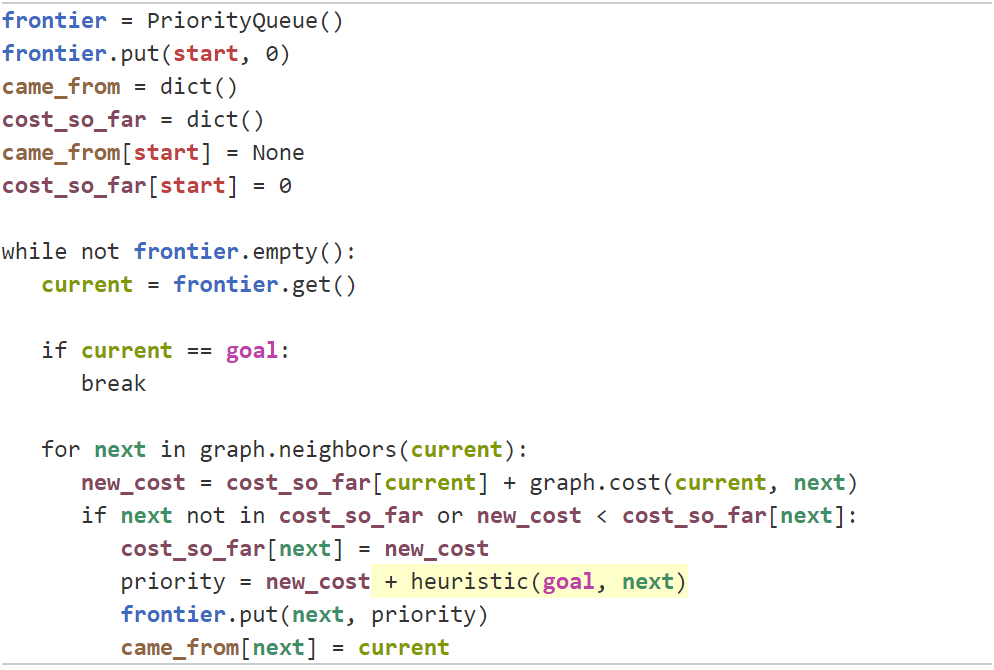
将加权有向图转为解空间树,逐步写出当前节点的拓展节点的g(n)、h(n)、f(n)并标在图的节点旁边
五、(20分)
分治算法的题,是作业题上的一道原题。
原题如下:

第一问写出算法思想
第二问写伪代码
第三问分析时间复杂度
算法思想:
首先利用O(nlogn)的排序算法对S进行排序;
然后循环遍历S的每一个元素S[i],利用二分查找判断S中是否包含x-S[i],该步二分查找复杂度为O(logn),因此循环复杂度为O(nlogn)
综上算法的整体复杂度为O(nlogn)
六、(15分)
贪心算法的题。(这道题我真是无力吐槽,考场上没看懂怎么写,考完之后问了几个同学都说贪心思想和算法随便写的,且每个人写的都不一样,后来问老师那个题怎么写,老师说只要言之有理都算对,,,)
题目大概写一下吧,反正我觉得这题出的真差,你们复习的时候可以自己找点别的贪心算法的题做。
有一条环形公路,公路上有n个加油站,一辆油箱容量无限大的汽车在这条路上行驶,每个加油站所能给车加的最大油量为si,车在每两个加油站之间行驶耗得油为ci。要求写出一个贪心算法,让这个车选择一个加油站作为起始点,能够成功绕这个环形公路一圈并回到起始点,如果没有这样的加油站,则返回-1,有则返回所选择的起始加油站的编号。
第一问写贪心思想
第二问证明贪心思想
第三问伪代码
第四问时间复杂度
贪心思想:
贪心思想的证明:
七、(10分)
动态规划的题。比较简单,多做几道动态规划的题应该就可以做出来了。
题目大致如下:
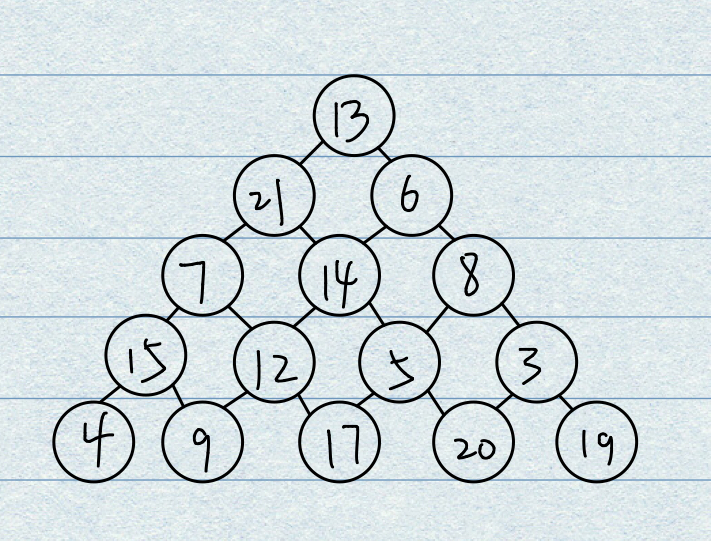
给定如图所示的一个树状图,每个节点上都标有该点权值,该树共有5层,从第一层的节点进入,从第五层的节点出来,要求找出一条长为4(即通过了5个节点)的路径,使得该条路径所经过的5个节点和最小。
图像大致如下: