最大连续子数组和(最大子段和)问题求解及自动测试
一、题目描述及求解思路
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
针对以上问题采用枚举法对数组求和每一种可能性进行比较,取最大值,其时间复杂度为O(n^2),具体调用函数代码如下:
int Maxsum(int arr[], int len)
{
int msum = 0;
int i;
int j;
int n = 0;
for (i = 0; i < len; i++)
{
int nsum = 0;
if (arr[i] >= 0)
n++;
for (j = i; j < len; j++)
{
nsum += arr[j];
if (nsum > msum)
msum = nsum;
}
}
if (n != 0)
return msum;
else
return 0;
}
- 代码地址:点击这里
二、覆盖选择及测试样例
调用函数Maxsum,其流程图如下图所示:
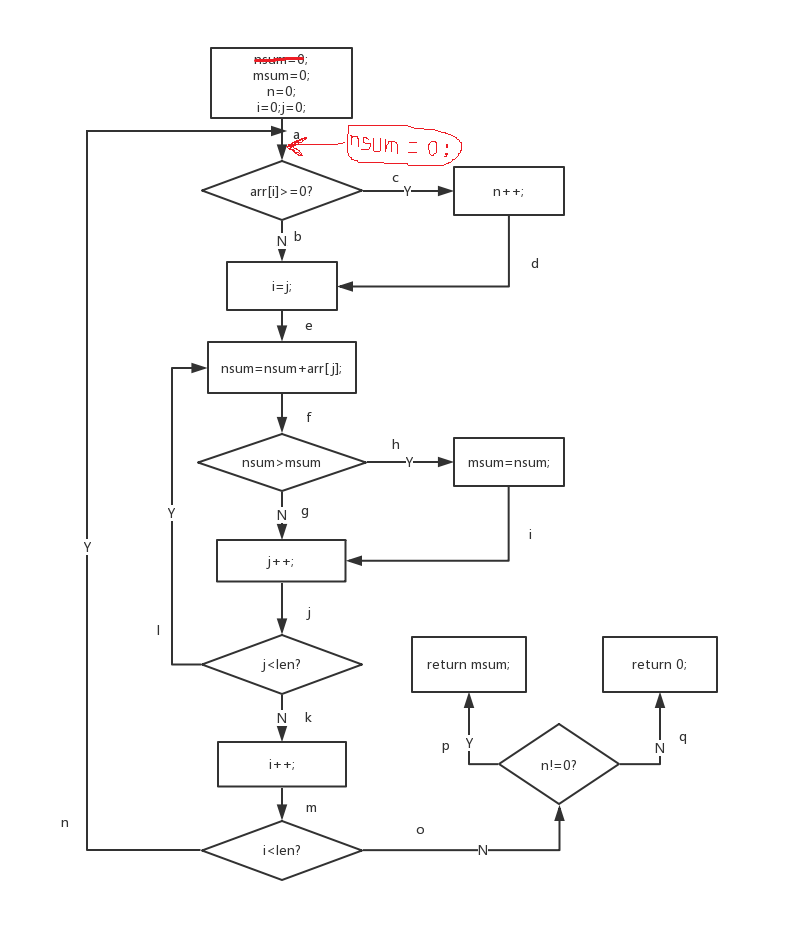
- 分析:
1,需要覆盖的路径分为a-b-g-k-n-q和a-c-h-l-o-p或a-b-g-k-n-p和a-c-h-l-o-q等14组;
2,需要满足的判定为:判定一(arr[i]>=0,arr[i]<0);判定二(nsum>msum,nsum<=msum);判定三(j<len,j>=len);
判定四(i<len,i>=len);判定五(n!=0,n==0)。 - 选择测试样例:
1,arr[]={-6,-13,-15,-2,-5,-4} ;覆盖路径a-b-g-k-n-q 满足arr[i]<0&&nsum<=msum&&j<len(j>=len)&&i<len(i>=len)&&n=0条件;
2,arr[]={1,2,3,10,4}; 覆盖路径a-c-h-l-o-p 满足arr[i]>=0&&nsum>msum&&j<len(j>=len)&&i<len(i>=len)&&n!=0条件;
三、自动测试
建立单元测试项目,编写测试代码,运行测试,结果如下图所示:
