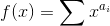HDU 4609 3-idiots

传送门

问给定n条小木棍 随机选3根构成三角形的概率

看起来和多项式没啥关系对不对 = =

但实际上它的确可以用多项式来做qaq

我们构造多项式

然后自乘一下就能得到两根木棍拼起来的方案数

然后枚举所有拼出来的长度 算一下>=这个长度的木棍个数

求出不能拼成三角形的方案数

然后最后用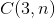减一减 除一除就可以了qwq

【注意sum的预处理范围是两倍权值T^T】

附代码。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
#define inf 20021225
#define db double
#define mxn 400010
using namespace std;

const db pi=acos(-1.0);

struct complex
{
    db x,y;
    complex(){}
    complex(db _x,db _y){x=_x,y=_y;}
}f[mxn],g[mxn];

complex operator +(complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+b.x*a.y);}
int rev[mxn];
int init(int n)
{
    int lim=1,l=0;
    while(lim<n)    lim<<=1,l++;
    for(int i=1;i<lim;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
    return lim;
}

void fft(complex *a,int n,int f)
{
    for(int i=1;i<n;i++)    if(rev[i]>i)
        swap(a[rev[i]],a[i]);
    for(int k=2;k<=n;k<<=1)
    {
        int mid = k>>1; complex Wn=complex(cos(pi/mid),f*sin(pi/mid));
        for(int i=0;i<n;i+=k)
        {
            complex w=complex(1.0,0.0);
            for(int j=0;j<mid;j++,w=w*Wn)
            {
                complex x=a[i+j],y=w*a[i+mid+j];
                a[i+j] = x+y; a[i+mid+j]= x-y;
            }
        }
    }
    if(f==-1)   for(int i=0;i<n;i++)    a[i].x=(a[i].x+0.5)/(db)n;
}
int n,a[mxn],sum[mxn];
ll ans;
void work()
{
    sort(a+1,a+n+1);
    for(int i=1;i<=n;i++)   f[a[i]].x++,g[a[i]*2].x++;
    //for(int i=0;i<=20;i++)    printf("%f %f
",f[i].x,f[i].y);
    int lim=init(200000);
    fft(f,lim,1);
    for(int i=0;i<lim;i++)  f[i]=f[i]*f[i];
    fft(f,lim,-1);
    for(int i=1;i<lim;i++)
    {
        //if(i<10)  printf("%d %.2f
",i,f[i].x);
        f[i].x-=g[i].x;
        ll tmp=f[i].x/2.0;
        ans+=(ll)tmp*(n-sum[i-1]);
        //if(tmp)	printf("%lld %d
",tmp,n-sum[i-1]);
        //if(i<10)  printf("%d %I64d %d
",i,tmp,calc(i)-2);
    }
    //printf("%lld
",ans);
    ans=(ll)n*(n-1ll)*(n-2ll)/6ll -ans;
    ll tot=(ll)n*(n-1ll)*(n-2ll)/6ll;
    printf("%.7lf
",(db)ans/tot);
}

void clear()
{
    memset(sum,0,sizeof(sum));
    for(int i=0;i<mxn;i++)  f[i]=complex(0,0),g[i]=complex(0,0);
    n=ans=0;
}

int main()
{
    int T;scanf("%d",&T);
    while(T--)
    {
        clear();
        scanf("%d",&n);
        for(int i=1;i<=n;i++)   scanf("%d",&a[i]),sum[a[i]]++;
        for(int i=1;i<=200000;i++)  sum[i]+=sum[i-1];
        work();
    }
    return 0;
}
/**
1
4
100000 100000 100000 100000
*/