斯坦福大学CS224d基础1：线性代数知识

斯坦福大学CS224d基础1：线性代数知识

作者：Zico Kolter (补充： Chuong Do)

翻译：@MOLLY(mollyecla@gmail.com) @OWEN 校正：@寒小阳(hanxiaoyang.ml@gmail.com) @龙心尘(johnnygong.ml@gmail.com)

2015年9月30日

1基本概念和符号    2

1.1基本符号    2

2 矩阵乘法    3

2.1向量的乘积    3

2.2矩阵-向量的乘积    4

2.3矩阵-矩阵乘积    5

3 运算和性质    6

3.1 单位矩阵与对角矩阵    6

3.2转置    7

3.3对称矩阵    7

3.4矩阵的迹    7

3.5范数    8

3.6线性无关和秩    9

3.7逆    9

3.8 正交矩阵    10

3.9矩阵的值域和零空间    10

3.10 行列式    11

3.11 二次型和半正定矩阵    13

3.12特征值和特征向量    14

3.13 对称矩阵的特征值和特征向量    15

4矩阵微积分    17

4.1梯度    17

4.2Hessian矩阵    18

4.3    二次函数或线性函数的梯度和Hessian矩阵    20

4.4最小二乘法    21

4.5行列式的梯度    21

4.6最优化特征值    22

 

1基本概念和符号

线性代数可以对一组线性方程进行简洁地表示和运算。例如，对于这个方程组:

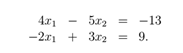
这里有两个方程和两个变量，如果你学过高中代数的话，你肯定知道，可以为x1 和x2找到一组唯一的解 (除非方程可以进一步简化，例如，如果第二个方程只是第一个方程的倍数形式。但是显然上面的例子不可简化，是有唯一解的)。在矩阵表达中，我们可以简洁的写作:

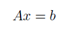
其中：

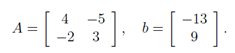
很快我们将会看到，咱们把方程表示成这种形式，在分析线性方程方面有很多优势(包括明显地节省空间)。

 

1.1基本符号

以下是我们要使用符号:

• 符号A ∈ R^m×n表示一个m行n列的矩阵，并且矩阵A中的所有元素都是实数。
  • 符号x ∈ Rⁿ表示一个含有n个元素的向量。通常，我们把n维向量看成是一个n行1列矩阵，即列向量。如果我们想表示一个行向量（1行n列矩阵），我们通常写作x^T (x^T表示x的转置，后面会解释它的定义)。
  • 一个向量x的第i个元素表示为x_i：

• 我们用a_ij (或A_ij，A_i，j，等) 表示第i行第j列的元素：

 

• 我们用a_j 或A_:，j表示A矩阵的第j列元素：

 

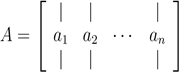
• 我们用a^T _i或 A_i，:表示矩阵的第i行元素:

  

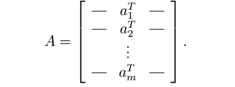
• 请注意，这些定义都是不严格的（例如，a₁和a₁^T在前面的定义中是两个不同向量）。通常使用中，符号的含义应该是可以明显看出来的。

2 矩阵乘法

矩阵 A ∈ R^m×n 和B ∈ R^n×p 的乘积为矩阵 ：

其中：

.

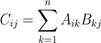请注意，矩阵A的列数应该与矩阵B的行数相等，这样才存在矩阵的乘积。有很多种方式可以帮助我们理解矩阵乘法，这里我们将通过一些例子开始学习。

 

2.1向量的乘积

给定两个向量x，y ∈ Rⁿ，那么x^T y的值，我们称之为向量的内积或点积。它是一个由下式得到的实数：

.

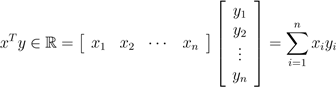可以发现，内积实际上是矩阵乘法的一个特例。通常情况下x^T y = y^T x。

对于向量x ∈ R^m， y ∈ Rⁿ（大小不必相同），xy^T ∈ R^m×n称为向量的外积。外积是一个矩阵，其中中的每个元素，都可以由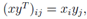得到，也就是说，

.

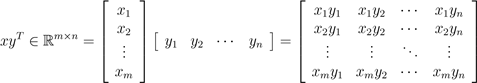我们举个例子说明外积有什么用。令1 ∈ Rⁿ 表示所有元素都是1的n维向量，然后将矩阵 A ∈ R^m×n 的每一列都用列向量x ∈ R^m表示。使用外积，我们可以将A简洁的表示为：

 

.

2.2矩阵-向量的乘积

对于一个矩阵A ∈ R^m×n 和向量x ∈ Rⁿ，他们的乘积为向量 y = Ax ∈ R^m。理解矩阵向量乘法的方式有很多种，我们一起来逐一看看。

以行的形式书写A，我们可以将其表示为Ax的形式：

.

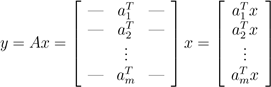也就是说，y第i行的元素等于A的第i行与x的内积 .

咱们换个角度，以列的形式表示A，我们可以看到：

.

换言之，y是A列的线性组合，线性组合的系数就是x的元素。

上面我们看到的是右乘一个列向量，那左乘一个行向量嘞？对于A ∈ R^m×n，x ∈ R^m， y ∈ Rⁿ，这个式子可以写成y^T = x^T A 。向之前那样，我们有两种方式表达y^T，这取决于表达A的方式是行还是列。第一种情况是把A以列的形式表示：

这个式子说明y^T 第i列的元素等于向量x与A的第i列的内积。

我们也一样可以把A表示成行的形式，来说明向量-矩阵乘积。

我们可以看到y^T 是A的行的线性组合，线性组合的系数是x的元素。

2.3矩阵-矩阵乘积

基于以上知识，我们可以看到如之前所定义的矩阵-矩阵乘法C=AB有四种不同（但是等价）的理解方法。

首先，我们可以将矩阵-矩阵相乘看作一组向量-向量乘积。根据其概念，我们最好理解的方式是矩阵C的(i，j)元素是A的i行与B的 j列的内积。符号表达如下：

.

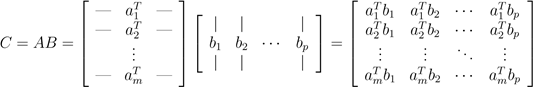注意由于A ∈ R^m×n ， B ∈ R^n×p， a_i ∈ Rⁿ b_j ∈ Rⁿ， 所以内积永远有意义。对矩阵乘法而言，以A的行和B的列表示是最"自然"的表示方法。当然，我们也可以以A的列和B的行的形式进行表示。表达方法是AB外积累加的形式，稍微复杂一点点。符号表达为：

 

.

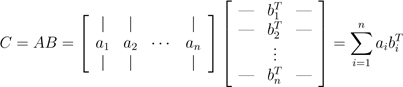换一种方式表达，AB的值等于对于所有的i，A的i列与B的i行的外积的和。因此，对于a_i ∈ R^m 和 b_i ∈ R^p，外积a_ib_i^T的维度是m×p，它与C的维度是相同的。等式可能有点难理解，花点时间想想，我猜你肯定能明白。

第二种理解方式是，我们也可将向量-向量乘法看做一系列的矩阵-向量乘积。具体来说，如果我们将B以列的形式表示，我们可以将C的每一列看做A和B列的矩阵-向量乘积。符号表达为：

 

.

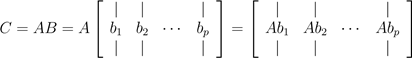可以将C的i列以矩阵-向量乘积（向量在右）的方式表示为c_i = Ab_i. 这些矩阵-向量乘积可以用前面的两种观点解释。最后类比一下，我们以A的行形式表示，将C的行视为A的行与C的矩阵-向量乘积，符号表达为

 

.

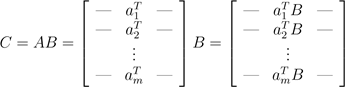在此，我们以矩阵-向量乘积（向量左乘）的形式表示了C的i列，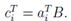

只是一个矩阵乘法而已，这么细的分析看上去好像没有必要，尤其是当我们知道矩阵乘法定义后其实很容易可以计算得到结果。然而，几乎所有的线性代数内容都在处理某种类型的矩阵乘法，因此花一些时间去形成对这些结论的直观认识还是很有帮助的。

此外，知道一些更高层次的矩阵乘法的基本性质也是有好处的：

• 结合律即(AB)C = A(BC)

• 分配率即A(B + C) = AB + AC
  • 注意哦，矩阵乘法没有交换律，即AB ≠BA.（例如，如果A ∈ R^m×n 和B ∈ R^n×q，矩阵的乘积BA在m和q不等时，BA可能根本就不存在）

如果你对这些性质不熟悉，最好花些时间自己证明一下。例如，为了验证矩阵乘法的结合律，对于A ∈ R^m×n， B ∈ R^n×p，C ∈ R^p×q，注意AB ∈ R^m×p，而 (AB)C ∈ R^m×q。类似的有BC ∈ R^n×q，所以A(BC) ∈ R^m×q。因此可以得到维度相同的矩阵。为了说明矩阵乘法符合结合律，证明(AB)C 第(i,j)个元素是否与A(BC)的(i,j)个元素相等就够了。我们可以直接运用矩阵乘法的定义进行证明。

上面的推导过程中，第一个和最后两个等式使用矩阵乘法的定义，第三和第五的等式使用标量乘法的分配率，第四个等式使用了标量加法的交换律和结合律。这种将运算简化成标量的特性以证明矩阵性质的方法会经常出现，你可以熟悉熟悉它们。

3 运算和性质

在这一节中，我们将介绍几种矩阵/向量的运算和性质。很希望这些内容可以帮助你回顾以前知识，这些笔记仅仅是作为上述问题的一个参考。

3.1 单位矩阵与对角矩阵

单位矩阵，记作I ∈ R^n×n， 是一个方阵，其对角线上的都是1，其他元素都是0。即：

它具备A ∈ R^m×n矩阵的所有性质

请注意，在某种意义上，标识矩阵的符号是有歧义的，因为它没有指定I的维度。一般而言，从上下文中可以推断出I的维度，这个维度使矩阵相乘成为可能。例如，在上面的等式AI = A中的I是n × n矩阵，而A = IA中 I是m × m矩阵。

对角矩阵除了对角线元素之外其他元素都是0。可以记作D = diag(d₁，d₂，...，d_n)，其中：

显然，I = diag(1，1，...，1).

3.2转置

矩阵的转置的是矩阵行和列的"翻转"。对于一个矩阵A ∈ R^m×n，，它的转置，A^T ∈ R^n×m，是一个n × m 的矩阵，其元素为

我们实际上已经使用转置当描述行向量的转置，因为一个列向量的转置，自然是一个行向量。

下面是一些关于转置的性质，证明起来也不太难：

• (A^T )^T = A
• (AB)^T = B^T A^T
• (A + B)^T = A^T + B^T

3.3对称矩阵

如果一个方阵A∈ R^n×n满足条件A = A^T，那么它就是对称的。如果满足A = −A^T则A是反对称的。很容易证明，任何矩阵A ∈ R^n×n，A + A^T 是对称的，而 A−A^T是反对称的。因此，任何方阵A ∈ R^n×n可以表示为一个对称矩阵和反对称矩阵的和，因为:

右边的第一个矩阵是对称的，第二个是反对称的。在实践中，对称矩阵是很常用的，他们有诸多优秀的性质，我们将在以后进行说明。我们通常将所有大小为n的对称矩阵的集合表示为Sⁿ；A ∈ Sⁿ则表示A是n × n的对称矩阵。

3.4矩阵的迹

方阵A ∈ R^n×n的迹，记作tr(A)，或可以省略括号表示成trA，是矩阵的对角线元素之和:

正如cs229讲义中所述，矩阵的迹具有以下性质（在此讲述完全是为了内容的完整性）：

• 对于A ∈ R^n×n， trA = trA^T .
• 对于A，B ∈ R^n×n， tr(A + B) = trA + trB.
• 对于A ∈ R^n×n， t ∈ R， tr(tA) = t trA.
• 对于方阵A,B,C，trABC = trBCA = trCAB，即使有更多的矩阵相乘，这个性质也不变.

前三个性质比较容易证明，咱们一起来看看第4个性质。假设A ∈ R^m×n ，B ∈ R^n×m (因此AB ∈ R^m×m是个方阵)。观察到BA ∈ R^n×n也是一个方阵，所以他的迹是有意义的。为了证明trAB = trBA，注意到：

 

在这里，第一个和最后两个等式使用了迹运算和矩阵乘法的定义。第四个等式是最重要的部分，它使用了标量乘法的交换性来交换每个乘积中因式顺序，也使用了标量加法的交换律和结合律将求和过程重新排序。

3.5范数

向量的范数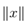是向量"长度"的非正式度量。例如，我们常用的欧氏或ℓ2范数。

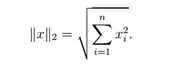
注意 .

更正式的来讲，范数是满足以下4个特性的任何一个方程f : Rⁿ → R:

1. 对于任意x ∈ Rⁿ， f(x) ≥ 0 (非负性).
2. 当且仅当x = 0 时，f(x) = 0(确定性).
3. 对于任意x ∈ Rⁿ，t∈ R，f(tx) = |t|f(x) (均匀性).
4. 对于任意 x，y∈Rⁿ，f(x + y)≤f(x) + f(y) (三角不等性).

另一个范数的例子是ℓ₁范数，

以及ℓ_∞范数，

事实上，这三个范数都是ℓ_P范数家族的的例子，它包含一个实参数p≥1。ℓ_P范数定义为：

.

也可以定义矩阵A的范数，如Frobenius范数，

.

也存在许多其他的范数，但它们超出了这篇综述讨论的范围。

 

3.6线性无关和秩

对于一组向量{x₁，x₂，...x_n} ∈ R^m，如果没有向量可以表示为其余向量的线性组合，这组向量就是（线性）无关的。相反，如果一个向量属于一个集合，这个集合中的向量可以表示为其余的向量某个线性组合，那么就称其称为向量（线性）相关。也就是说，对于一些标量值α₁，...，α_n−1 ∈ R，如果

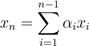
我们说向量x₁，...，x_n是线性相关；否则，该向量线性无关。例如，向量

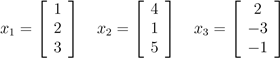
是线性相关的，因为x₃ = −2x₁ + x₂.

矩阵A ∈ R^m×n的列秩是所有线性独立的列的最大子集的大小。由于某些术语的滥用，列秩通常指矩阵A线性无关的列的数目。相似的，将A的行构成一个线性无关集，行秩是它行数的最大值。

对任意矩阵A ∈ R^m×n，其列秩与行秩是相等的（虽然我们不打算证明），所以我们将两个相等的秩统称为A的的秩。秩的一些基本性质如下：

• 对于 A ∈ R^m×n， rank(A) ≤ min(m，n). 如果rank(A) = min(m，n)， 则称A满秩。
• 对于 A ∈ R^m×n， rank(A) = rank(A^T ).
• 对于 A ∈ R^m×n， B ∈ R^n×p， rank(AB) ≤ min(rank(A)，rank(B)).
• 对于 A，B ∈ R^m×n， rank(A + B) ≤ rank(A) + rank(B).

3.7逆

矩阵A ∈ R^n×n的逆，写作A⁻¹，是一个矩阵，并且是唯一的。

A⁻¹A = I = AA⁻¹.

注意不是所有的矩阵都有逆。例如非方阵，是没有逆的。然而，即便对于一些方阵，它仍有可能不存在逆。如果A⁻¹存在，我们称矩阵A 是可逆的或非奇异的，如果不存在，则称矩阵A不可逆或奇异。

如果一个方阵A有逆A⁻¹，它必须满秩。我们很快可以看到，除了满秩，矩阵可逆还有许多充分必要条件。

满足以下的性质的矩阵可逆；以下所有叙述都假设A，B ∈ R^n×n是非奇异的：

• (A⁻¹)⁻¹ = A
• (AB)⁻¹ = B⁻¹A⁻¹
• (A⁻¹)^T = (A^T )⁻¹. 因此这样的矩阵经常写作A^−T

举一个矩阵的逆的应用实例。对于线性方程组Ax = b，其中 A ∈ R^n×n，并且x，b ∈ Rⁿ.如果A是非奇异（即可逆），则x = A⁻¹b（如果A ∈ R^m×n不是方阵呢？是否成立？）

3.8 正交矩阵

如果x^T y = 0，则两个向量 x，y ∈ Rⁿ是正交的。对于一个向量x ∈ Rⁿ，如果则是x归一化的。对于一个方阵U ∈ R^n×n，如果所有列都是彼此正交和归一化的，（列就称为标准正交）则这个方阵是正交的（注意在讨论向量或矩阵时，正交具有不同的含义）。

根据正交和归一化的定义可得：

U^T U = I = UU^T

换言之，一个正交矩阵的逆矩阵的是它的转置。注意，如果U不是方阵的，也就是说， U ∈ R^m×n，n < m，但它的列仍然是正交的，则U^T U = I，但UU^T ≠ I.等。我们一般只使用正交这个术语来描述U为方阵的情形。

另一个正交矩阵的很好的属性是，向量与正交矩阵的运算将不会改变其欧氏范数，即对于任意x ∈ Rⁿ，正交的U ∈ R^n×n：

3.9矩阵的值域和零空间

一组向量{x₁，x₂，...x_n}的值域是{x₁，x₂，...x_n}线性组合的所有向量的集合。即

可以看出如{x₁，...，x_n}是一组n个线性无关的向量，其中x_i ∈ Rⁿ，则({x₁，...x_n}) 的值域= Rⁿ。换句话说，任何向量v ∈ Rⁿ可以写成x₁ 至 x_n的线性组合。向量y ∈ R^m 在值域 {x₁，...，x_n}上的投影 (假定 x_i ∈ R^m) 是向量v ∈ span({x₁，...x_n})，则通过比较其欧式范数，v 与 y无限接近。这个投影记作Proj（Y；{ x1，…，n}）,可以定义它为，

A ∈ R^m×n的值域（有时也被称为列空间），表示为R(A)，就是A的值域。换言之，

R(A) = {v ∈ R^m : v = Ax，x ∈ Rⁿ}.

我们假设A满秩且n < m，向量y ∈ R^m 在A值域上面的投影可以表示为

这最后一个方程应该看起来非常熟悉，因为它几乎是我们在课上用于参数的最小二乘估计公式（并且我们可以快速再次推导出来）几乎相同的。看一下投影的定义，你会发现这其实与我们在解决最小二乘法问题时进行最小化的目的是相同的（除了范数是一个平方，这并不影响求得最优的点），所以这些问题是有自然联系的。当 A 仅含有1个单独的列 a ∈ R^m，则出现了向量在一条直线上投影的特殊情况。

矩阵A ∈ R^m×n的零空间，记为N(A)，是被A乘后，得到的所有等于0的向量一个集合，即，

N(A) = {x ∈ Rⁿ : Ax = 0}.

注意，向量R(A)的大小为m，而N(A)的大小为n，所以 R(A^T ) 和 N(A) 的向量都在 Rⁿ中。事实上，我们可以讨论更多。

换句话说，R(A^T ) 和 N(A)是不相交的子集，一同跨越了Rⁿ整个空间。这种类型的集合称为正交互补，写作R(A^T ) = N(A)^⊥.

3.10 行列式

方阵A∈R^n×n的行列式是一个映射det: R^n×n→R,记作|A|或det A (同迹运算一样，我们通常省略括号)。在代数上,可以显式地写出A的行列式的公式，但是很遗憾，它的意义不够直观。咱们先给出行列式的几何解释，然后再探讨一下它的一些特殊的代数性质。

对于矩阵：

考虑由A中所有行向量a1,a2,..,an的所有可能线性组合组成的点集S⊂Rⁿ，其中线性组合的参数都介于0和1之间；换句话说，由于这些线性组合的参数a1,a2,...,an∈Rⁿ满足0≦ai≦1,i=1,...,n，集合S是张成子空间({a1, . . , an})的约束。公式表达如下：

A的行列式的绝对值，是集合S的"体积"的一个量度。

例如，考虑2×2矩阵，

此处，矩阵的行：

对应于这些行的集合S如图1所示。对于二维矩阵，S一般是平行四边形。在我们的示例中A的行列式的值为|A| = -7.(可以使用本节后文将给出的公式来计算)。所以平行四边形的面积为7（自行证明！）

在三维中，集合S对应一个平行六面体（一个三维的斜面的盒子，例如每一面都是平行四边形）。这个3×3矩阵的行列式的绝对值，就是这个平行六面体的三维体积。在更高的维数中，集合S是一个n维超平形体。

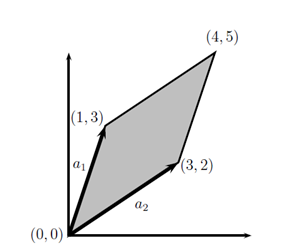
图 1 ：公式(1)给出2×2矩阵A的行列式图示。此处，a1和a2是对应于A中的行的向量，集合S对应于阴影区域（亦即平行四边形）。行列式的绝对值，|det A|=7，是平行四边形的面积

 

代数上，行列式满足下列三个性质（其它性质亦遵循它，包括行列式的一般公式）

1、单位矩阵的行列式为1 ，|I| = 1。(从几何上来看，单位超立方体的体积为1)。

2、对于一个矩阵A∈R^n×n，如果将A中某行乘以一个标量t∈R，新矩阵的行列式值为t|A|。

(几何上，集合S的一条边乘以因数t，会导致体积扩大t倍)

3、我们交换行列式A任意两行a^T_i和a^T_j，新矩阵的行列式的值为-|A|,例如：



满足上述三个条件的函数是否存在，并不是那么容易看出来的。然而事实上，此函数存在且唯一。(此处不证明)

这三个性质的推论包括：

• 对于 A ∈ R^n×n, |A| = |A^T |。
• 对于 A,B ∈ R^n×n, |AB| = |A||B|。
• 对于 A ∈ R^n×n,当且仅当A奇异(即不可逆)时，|A| = 0。（如果A奇异，它必不满秩，它的列线性相关。此时，集合S对应于n维空间中的一个平板，因此体积为零。）
• 对于A ∈ R^n×n，且A非奇异, |A^-1| = 1/|A|.

在给出行列式的一般定义之前,我们定义代数余子式：对于A∈ R^n×n，矩阵A_i,j ∈R^(n-1)×(n-1)是A删除i行和j列的结果。

行列式的一般（递推）定义：

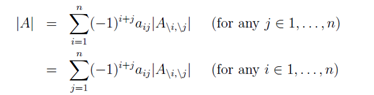
其中首项A∈ R^1×1的行列式，|A| = a₁₁。如果我们把公式推广到A∈ R^n×n，会有n！（n的阶乘）个不同的项。因此，我们很难显式地写出3阶以上的矩阵的行列式的计算等式。

然而，3阶以内的矩阵的行列式十分常用，大家最好把它们记住。

矩阵A∈ R^n×n的古典伴随矩阵（通常简称为伴随矩阵），记作adj(A),定义为：

（注意A的系数的正负变化。）可以证明，对于任意非奇异矩阵A∈ R^n×n，有

这个式子是求矩阵的逆的一个很好的显示公式。大家要记住，这是一个计算矩阵的逆的一个更加高效的方法。

3.11 二次型和半正定矩阵

对于一个方阵A∈ R^n×n和一个向量x∈ Rⁿ，标量x^TAx被称作一个二次型。显式地写出来，我们可以看到：

注意：

第一个等式是由标量的转置等于它自身得到，第二个等式是由两个相等的量的平均值相等得到。由此，我们可以推断，只有对称分量对二次型有影响。我们通常约定俗成地假设二次型中出现的矩阵是对称矩阵。

我们给出如下定义：

• 对于任一非零向量x∈Rⁿ，如果x^TAx>0，那么这个对称矩阵A∈Sⁿ是正定（PD）的.通常记作A≻0，(或简单地A>0)，所有的正定矩阵集合记作Sⁿ₊₊。

• 对于任一非零向量x∈Rⁿ，如果x^TAx≧0，那么这个对称矩阵A∈Sⁿ是半正定（PSD）的。记作A≽0，(或简单地A≧0)，所有的半正定矩阵集合记作Sⁿ₊ 。

• 同样的，对于任一非零向量x∈Rⁿ，如果x^TAx＜0,那么这个对称矩阵A∈Sⁿ是负定(ND)的。记作A≺0，(或简单地A＜0)。

•对于任一非零向量x∈Rⁿ，如果x^TAx≤0,那么这个对称矩阵A∈Sⁿ是半负定（NSD）的.记作A≼0，(或简单地A≤0)。

•最后，如果它既不是半正定也不是半负定-亦即，存在x₁，x₂∈Rⁿ使得x₁^TAx₁>0且x₂^TAx₂<0，那么对称矩阵A∈Sⁿ是不定矩阵。

显然，如果A是正定的，那么-A是负定的，反之亦然。同样的，如果A是半正定的，那么-A是半负定的，反之亦然。如果A是不定的，-A也是不定矩阵。

正定矩阵和负定矩阵的一个重要性质是，它们一定是满秩的。因此，也是可逆的。为了证明这个性质，假设存在矩阵A∈ R^n×n是不满秩的。进而，假设A的第j列可以其它n-1列线性表示。

对于x₁,...,x_j−1, x_j+1,...,x_n ∈R,设x_j=-1，我们有

但是这意味着对于某些非零向量x，x^TAx=0，所以A既不能正定，也不能负定。因此，如果A是正定或者负定，它一定是满秩的。

最后，一种常见的正定矩阵需要注意：给定一个矩阵A ∈R^m×n (不一定是对称，甚至不一定是方阵)，矩阵G=A^TA(有时也称为格拉姆矩阵)必然是半正定的。进一步，如果m≥n,(为了方便，我们假设A满秩)此时，G=A^TA是正定的。

3.12特征值和特征向量

对于一个方阵A ∈R^n×n，如果：

我们说λ∈C是A的特征值，x∈Cⁿ是对应的特征向量.

直观上看，其实上面的式子说的就是A乘一个向量x，得到的新的向量指向和x相同的方向，但是须乘一个标量λ。注意对任一个特征向量x∈Cⁿ和标量t∈C，A(cx) = cAx = cλx = λ(cx),，所以cx也是一个特征向量。因此，我们要说λ所对应的特征向量。我们通常假设特征向量被标准化为长度1。(此时依然有歧义，因为x和-x都可以是特征向量，但是我们也没什么办法)。

如果

我们可以把上文的等式换一种写法，表明(λ,x)是A的一个特征值-特征向量对。 

但是当且仅当有非空零空间时，也就是当(λI − A)非奇异时，亦即

时，(λI − A)x = 0有x的非零解。

我们现在可以用前文的行列式的定义，来把这个表达式展开为一个(非常大的) λ的多项式，其中λ的最高阶为n。我们可以解出多项式的n个根(这可能十分复杂)，来得到n个特征值λ₁, ...，λ_n。 为了解出特征值对应的特征向量，我们可以简单地求线性等式(λ_iI − A)x = 0的解。需要注意，实际操作时，计算特征值和特征向量不用这个方法。(行列式的完全展开式有n!项）。这只是一个数学论证。

下面是特征值和特征向量的性质（假设A∈ R^n×n，且特征值λ₁,...，λ_n对应的特征向量为x₁,...，x_n）:

• 矩阵A的迹等于特征值的和

• A的行列式等于特征值的积

• A的秩等于A的非零特征值的个数。
• 如果A是非奇异矩阵，则1/λ_i是矩阵A^-1对应于特征向量x_i的特征值。亦即，A⁻¹x_i = (1/λ_i)x_i。（证明方法是，对于特征向量等式，Ax_i = λ_ix_i，在两边同时左乘A^-1）
• 对角矩阵D=diag(d₁, . . . ，d_n)的特征值是所有的对角元素。

    我们可以把所有的特征向量等式联立为

X ∈R^n×n 的列是A的特征向量，∧是对角元素为A的特征值的对角矩阵。亦即：

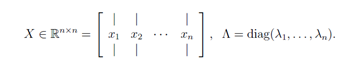
如果A的特征向量线性无关，则矩阵X可逆，所以A=X∧X^-1。可以写成这个形式的矩阵A被称作可对角化。

3.13 对称矩阵的特征值和特征向量

当我们考察对称矩阵A∈Sⁿ的特征值和特征向量时，有两个特别的性质需要注意。首先，可以证明，A的所有特征值都是实数。其次，A的所有特征向量时正交的。也就是说，上面所定义的矩阵X是正交矩阵。（我们把此时的特征向量矩阵记作U）。

接下来，我们可以将A表示为A=U∧U^T，由上文知，一个正交矩阵的逆等于它的转置。

    由此，我们可以得到所有完全使用特征值来定义的矩阵。假设A∈Sⁿ= U∧U^T。有：

其中，y=U^Tx（由于U满秩，任意y∈Rⁿ可以表示为此形式。）由于y_i²永远为正，这个表达式完全依赖于λ_i。如果所有的λ_i>0,那么矩阵正定；如果所有的λ_i≥0，矩阵半正定。同样的，如果所有的λ_i<0或λ_i≤0，矩阵A分别负定和半负定。最后，如果A既有正的特征值又有负的特征值，它是不定矩阵。

    特征值和特征向量的一个常见的应用是找出矩阵的某个函数的最大值。例如，对于矩阵A∈Sⁿ,考虑这个求最大值问题：

也就是说，我们希望找到使二次型最大的单位向量。假设特征值大小为λ₁ ≥ λ₂ ≥ . . . ≥ λ_n，这个最优化问题的最优解x为x₁，对应的特征值为λ₁.此时，二次型的最大值是λ₁。相似的，最小值问题的最优解

是x_n，对应的特征值是λ_n，那么最小值是λ_n。可以通过将A表示为特征向量-特征值的形式，然后使用正定矩阵的性质证明。然而，在下一节我们可以使用矩阵微积分直接证明它。

4矩阵微积分

之前章节的内容，在一般线性代数的课程中都会讲到。而有些常用的内容是没有的，这就是把微积分推广到向量。事实上，我们应用的微积分都会比较繁琐，各种符号总是让问题变得更复杂。在本节中，将给出一些矩阵微积分的基本定义，并举例说明。

4.1梯度

设 ƒ:R^m×n→R是大小为m×n的矩阵A的函数，且返回值为实数。ƒ 的梯度（关于A∈R^m×n）是一个偏导矩阵，定义如下：

 

即,一个m×n矩阵，其中

注意∇_Af(A)和A有相同的大小。所以，特别的，当A是一个向量x∈Rⁿ时，

需要特别记住的是，函数的梯度只在函数值为实数的时候有定义。也就是说，函数一定要返回一个标量。例如，我们就不能对Ax，A∈R^n×n中的x求梯度，因为它是一个向量。

它遵循和偏导相同的性质：

 

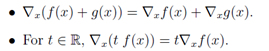
原则上，梯度是多变量函数偏导的延伸。然而，实际应用梯度时，会因为数学符号而变得棘手。例如，假设A∈R^m×n是一个具有固定系数的矩阵，b∈R^m是一个固定系数的向量。令ƒ ：R^m→R为由ƒ(z)=z^Tz，因此∇_zf(z) =2z。现在，考虑表达式;

∇f(Ax)

上式该如何理解？至少有两种解释：

1. 解释一，因∇f(Ax). = 2z,所以可将∇f(Ax).理解为点Ax处的梯度，那么：    

   ∇f(Ax) = 2(Ax) = 2Ax ∈ R^m

2. 解释二，可以认为f(Ax)是关于变量x的函数。正式的表述为，令g(x) = f(Ax)。那么在此种解释下有：

   ∇f(Ax) = ∇xg(x) ∈ Rⁿ

   大家可以发现，这两种解释确实不同。解释一得出的结果是m维向量，而解释二得出n维向量！怎么办？

   这里的关键是确定对那个变量求微分。在第一种情况下，是让函数f对参数z求微分，然后代入参数Ax。第二种情况，是让复合函数g（x）= F（AX）与直接对x求微分。第一种情况记为∇_zf（AX），第二种情况记为∇_xf（AX）。你会在作业中发现，理清数学符号是非常重要的。

   4.2Hessian矩阵

   假设 ƒ ：Rⁿ→R    是n维向量A的的函数，并返回一个实数。那么x的Hessian矩阵是偏导数的n×n矩阵，写作∇²_xf（x），简记为H。

   

    

   换句话说，∇²_xf(x) ∈ R^n×n ，其中：

   

   需要注意的是Hessian矩阵始终是对称的，即：

   

   和梯度类似，Hessian矩阵只在f(x)为实数时有定义。

   可以很自然联想到，偏导类似于函数的一阶导数，而Hessian类似函数的的二阶导数（我们使用的符号，也表明了这种联系）。通常这种直觉是正确的，但有些注意事项需要牢记。

   首先，只有一个变量的实值函数，f : R→R，它的基本定义是二阶导数是一阶导数的导数，即：

   

   然而，对于关于向量的函数，该函数的梯度是一个向量，我们不能取向量的梯度，即;

   

   并且这个表达式没有定义。因此，不能说Hessian矩阵是梯度的梯度。然而，在下面的意义上比较靠谱：如果我们取第i项（∇_xf（X））_i =∂F（X）/∂x_i，并取对x的梯度，我们得到：

   

   这是Hessian矩阵的第i列（或行）。 因此：

   

   如果此处稍粗略一点，可以得出，只要将其真实的含义理解为对 (∇_xf(x))的每一项求梯度，而不是对向量求梯度即可。

   最后注意，虽然可求出对矩阵A∈Rⁿ的梯度，但在本课程中，将只考虑向量x∈Rⁿ的Hessian矩阵。这仅仅是为了方便起见（而事实上，没有计算需要求矩阵的Hessian矩阵），因为矩阵的Hessian矩阵必须表示为所有的偏导数∂²f（A）/（∂A_ij∂A_kℓ），而要表示为矩阵却相当麻烦。

   4.3    二次函数或线性函数的梯度和Hessian矩阵

   现在，让我们确定一些简单函数的梯度和Hessian矩阵。应当指出的是，这里给出的所有的梯度都是在CS229讲义给出的特殊情况。

   当x∈Rⁿ，对于已知向量b∈Rⁿ，令f（X）= b^T x。 得：

   

   因此

   

   由此不难看出，∇_xb^T x= b。这是与单变量微积分类似的情况，其中，∂/（∂x）aX =a。

   现在考虑二次函数f（x）= x^TAx ,A∈Sⁿ。注意到：

   

   求其偏导数，分别考虑包含X_k和x_k²因子的项：

   

   其中最后一个等式是因为A是对称的（完全可以假设，因为它是二次型）。注意，∇_xf（x）的第k项只是A的第k行和x的内积。因此，∇_xx^TAx=2AX。同样，与单变量微积分类似，即∂/（∂x）    ax²= 2aX。

   最后，再看二次函数f（X）= x^TAx的Hessian矩阵（显然，线性函数b^T x的Hessian矩阵为零）。 在这种情况下，

   

   因此，应当清楚的是∇_x²x^TAx=2A，这完全是可证明的（并再次类似于单变量的情况∂²/(∂x²) ax² = 2a）。

   总之：

   ∇_xb^T x = b

   ∇_xx^TAx = 2Ax ( A 为对称矩阵)

   ∇_x²x^TAx = 2A ( A 为对称矩阵)

   4.4最小二乘法

   这里将用最后一节得到的公式推导最小二乘方程。假设对矩阵A∈R^m×n（为简单起见，假定A是满秩）和向量b∈R^m    ，使得b错误!未找到引用源。R（A）。在这种情况下，无法找到一个向量x∈Rⁿ，使得Ax = b。退一步，我们找一个向量x∈Rⁿ，使得Ax是尽可能接近b，即欧氏范数||Ax - b||₂²。

   且知||x||₂²=x^Tx，有：

   

   取对已有x的梯度，并使用上一节推出的性质

   

   让最后一个表达式等于零，并求解X满足的标准方程

   

   这正和我们课上推导的一样。

   4.5行列式的梯度

   现在考虑一种情况，求函数对矩阵的梯度，即对A∈R^n×n，求∇_A| A |。回顾之前关于行列式的讨论：

   

   因此：

   

   根据伴随矩阵的性质，可立即得出：

   

   现在，考虑函数f : Sⁿ ₊₊ → R, f(A) = log |A|，需要注意的是，一定要限制f的域是正定矩阵，因为这将确保| A | >0，这样log| A |是一个实数。在这种情况下，我们可以使用链式法则（很简单，只是单变量微积分的普通链式法则）得出：

   

   那么，很显然：

   

   此处，在最后一个表达式中去掉了转置符，因为A是对称的。注意当∂/(∂x) log x = 1/x时,和单值情况相似。

   4.6最优化特征值

   最后，通过直接分析特征值/特征向量，用矩阵微积分来解决一个优化问题。接下来，考虑等式约束优化问题：

   

   对于一个对称矩阵A ∈ Sⁿ，解决等式约束优化问题的标准方法是构造拉格朗日（一个包括等式约束的目标函数）。这种情况下的拉格朗日可由下式给出：

   

   其中λ被称为与等式约束对应的拉格朗日乘子。对这问题可以找到一个x*的最佳点，让拉格朗日的梯度在x*上为零（这不是唯一的条件，但它是必需的）。 即：

   

   注意，这其实是线性方程组Ax =λx。这表明，假设x^T x = 1，使x^T Ax最大化或（或最小化）的唯一的点正是A的特征向量。