Non-local Neural Networks

转载原文链接：https://blog.csdn.net/elaine_bao/article/details/80821306 欢迎前往原博客，这里仅仅当学习使用；

参考：https://zhuanlan.zhihu.com/p/33345791

————————————————
版权声明：本文为CSDN博主「Elaine_Bao」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/elaine_bao/article/details/80821306

Paper：https://arxiv.org/abs/1711.07971v1
Author：Xiaolong Wang, Ross Girshick, Abhinav Gupta, Kaiming He (CMU, FAIR)

0.简述
convolution和recurrent都是对局部区域进行的操作，所以它们是典型的local operations。受计算机视觉中经典的非局部均值（non-local means）的启发，本文提出一种non-local operations用于捕获长距离依赖（long-range dependencies），即如何建立图像上两个有一定距离的像素之间的联系，如何建立视频里两帧的联系，如何建立一段话中不同词的联系等。
non-local operations在计算某个位置的响应时，是考虑所有位置features的加权——所有位置可以是空间的，时间的，时空的。这个结构可以被插入到很多计算机视觉结构中，在视频分类的任务上，non-local模型在Kinetics和Charades上都达到了最好的结果。在图像识别的任务上，non-local模型提高了COCO上物体检测／物体分割／姿态估计等任务的结果。

1. Non-local Neural Networks

1.1 定义

按照非局部均值的定义，我们定义在深度神经网络中的non-local操作如下：

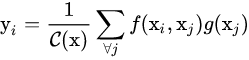                   （1）

其中x表示输入信号（图片，序列，视频等，也可能是它们的features），y表示输出信号，其size和x相同。f(xi,xj)用来计算i和所有可能关联的位置j之间pairwise的关系，这个关系可以是比如i和j的位置距离越远，f值越小，表示j位置对i影响越小。g(xj)用于计算输入信号在j位置的特征值。C(x)是归一化参数。

从上式中可以看出任意位置上的j，可以是时间的、空间的、时空的任意位置，都可以影响到i的输出值。作为对比，conv的操作是对一个局部邻域内的特征值进行加权求和，比如kernel size=3时，i−1≤j≤i+1。 recurrent的操作则是i时刻的值仅基于当前时刻或前一时刻（j=i or i-1）。

另外作为对比，non-local的操作也和fc层不同。公式(1)计算的输出值受到输入值之间的关系的影响（因为要计算pairwise function），而fc则使用学习到的权重计算输入到输出的映射，在fc中xjxj和xixi的关系是不会影响到输出的，这一定程度上损失了位置的相关性。另外，non-local能够接受任意size的输入，并且得到的输出保持和输入size一致。而fc层则只能有固定大小的输入输出。

non-local是一个很灵活的building block，它可以很容易地和conv、recurrent层一起使用，它可以被插入到dnn的浅层位置，不像fc通常要在网络的最后使用。这使得我们可以通过结合non-local以及local的信息构造出更丰富的结构。

1.2 表示形式

接下来我们会讨论f和g的几种形式。有意思的是我们的实验显示不同的表现形式其实对non-local的结果并没有太大影响，表明non-local这个行为才是主要的提升因素。

为了简化，我们只考虑g是线性的情况，即 ，其中Wg是一个可学的权重矩阵，实际中是通过空间域的1*1 conv或时空域的1*1*1 conv实现的。

接下来我们讨论f的不同形式：

Gaussian。从非局部均值和双边滤波器来看，常见的f是高斯函数。在本文中，我们考虑f为如下形式：

其中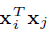是点乘相似度（dot-product similarity）。也可以用欧式距离，但是点乘在深度学习平台上更好实现。此时归一化参数为：。

Embedded Gaussian。高斯函数的一个简单的变种就是在一个embedding space中去计算相似度，在本文中，我们考虑以下形式：

其中和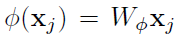是两个embedding。归一化参数和之前一致，为。

我们发现self-attention模块其实就是non-local的embedded Gaussian版本的一种特殊情况。对于给定的i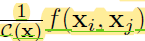，就变成了计算所有j的softmax，即，这就是[47]中self-attention的表达形式。这样我们就将self-attention模型和传统的非局部均值联系在了一起，并且将sequential self-attention network推广到了更具一般性的space/spacetime non-local network，可以在图像、视频识别任务中使用。

另外和[47]的结论不同，我们发现attention的形式对于我们研究的case来说并不是必须的。为了说明这一点，我们给出另外两种f的表达形式。

Dot product。 f也可以定义成点乘相似度，即：

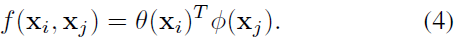
这里我们使用embedded version。在这里，归一化参数设为C(x)=N，其中N是x的位置的数目，而不是f的和，这样可以简化梯度的计算。这种形式的归一化是有必要的，因为输入的size是变化的，所以用x的size作为归一化参数有一定道理。

dot product和embeded gaussian的版本的主要区别在于是否做softmax，softmax在这里的作用相当于是一个激活函数。
Concatenation。 Concat是在Relation Networks [38]中用到的pairwise function。我们也给出了一个concat形式的f，如下：

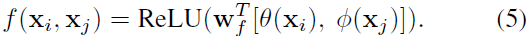
 里[.,.]表示的是concat，Wf是能够将concat的向量转换成一个标量的权重向量。这里设置C(x)=N。 

————————————————

以上我们定义了多种变种的pairwise function f，这说明了我们的non-local的灵活性，我们相信也会有别的变种能够提升性能。

1.3 Non-local Block

我们将(1)式中的non-local操作变形成一个non-local block，以便其可以被插入到已有的结构中。
我们定义一个non-local block为：

其中yi已经在(1)式中给出了，+xi则表示的是一个residual connection。residual connection的结构使得我们可以在任意的pretrain模型中插入一个新的non-local block而不需要改变其原有的结构（如Wz=0作为初始化则完全和原始结构一致）。
一个示例的non-local block如图所示，我们看到式(2),(3),(4)中的这些pairwise function可以通过矩阵乘法来进行，(5)则可以直接concat得到。

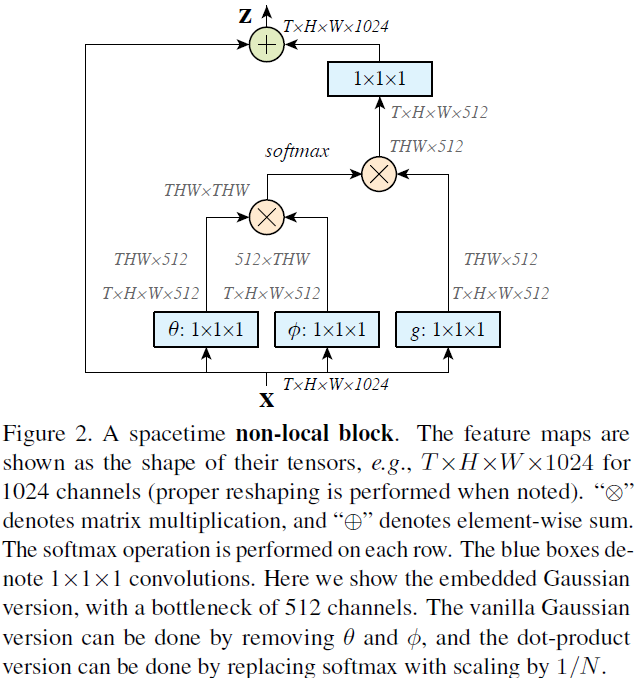
non-local block的pairwise的计算可以是非常lightweight的，如果它用在高层级，较小的feature map上的话。比如，图2上的典型值是T=4，H=W=14 or 7。通过矩阵运算来计算parwise function的值就和计算一个conv layer的计算量类似。另外我们还通过以下方式使其更高效。

Non-local Blocks的高效策略。我们设置Wg,Wθ,Wϕ的channel的数目为x的channel数目的一半，这样就形成了一个bottleneck，能够减少一半的计算量。Wz再重新放大到x的channel数目，保证输入输出维度一致。
还有一个subsampling的trick可以进一步使用，就是将(1)式变为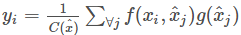：，其中x^是x下采样得到的（比如通过pooling），我们将这个方式在空间域上使用，可以减小1/4的pairwise function的计算量。这个trick并不会改变non-local的行为，而是使计算更加稀疏了。这个可以通过在图2中的ϕ和g后面增加一个max pooling层实现。

我们在本文中的所有non-local模块中都使用了上述的高效策略。一般只在高阶语义层中引入non-local layer，不然计算量会很大。

在tensorflow和pytorch中，batch matrix multiplication可以用matmul函数实现。在keras中，可以用batch_dot函数或者dot layer实现。

具体可以参考：

keras：titu1994/keras-non-local-nets​github.com

pytorch：AlexHex7/Non-local_pytorch​github.com

跟全连接层的联系

我们知道，non-local block利用两个点的相似性对每个位置的特征做加权，而全连接层则是利用position-related的weight对每个位置做加权。于是，全连接层可以看成non-local block的一个特例：

• 任意两点的相似性仅跟两点的位置有关，而与两点的具体坐标无关，即 
• g是identity函数， 
• 归一化系数为1。归一化系数跟输入无关，全连接层不能处理任意尺寸的输入。

跟Self-attention[2]的联系

这部分在原文中也提到了。Embedding的1*1卷积操作可以看成矩阵乘法：

于是，

这就是那篇名字很6的文章[2]提出来的self-attention。