目录
第1章计算公式
1.1 角度前方交会
 1.1.1 公式推导
1.1.1 公式推导
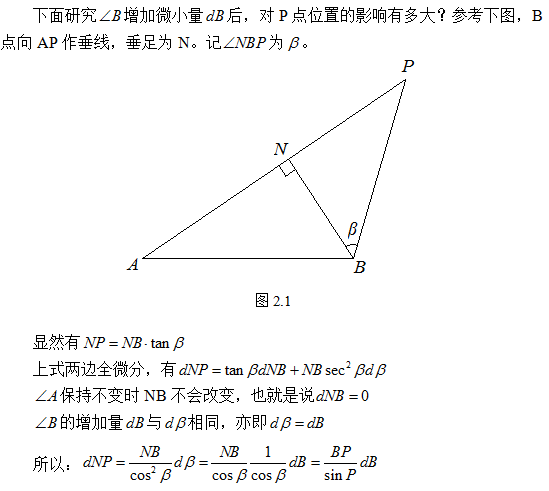
为了下面讨论的方便,这里对A、B、P的顺序进行了约定:A、B、P的排列顺序必须与方位角的增加方向一致。下图是数学系,方位角增加方向是逆时针,因此A、B、P为逆时针排列。

图1.1
下图是测量系,方位角增加方向是顺时针,因此A、B、P为顺时针排列。
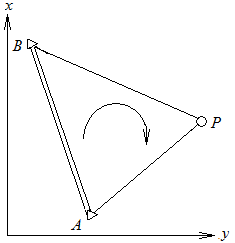
图1.2


1.1.2 验证代码
验证上面公式的C代码如下:
|
srand(time(NULL)); double xA = rand(); double yA = rand(); double xB = rand(); double yB = rand(); double xP = rand(); double yP = rand(); double sign = 1.0; double A = atan2(yP - yA,xP - xA) - atan2(yB - yA,xB - xA); double B = atan2(yA - yB,xA - xB) - atan2(yP - yB,xP - xB); if((yP - yA) * (xB - xA) - (xP - xA) * (yB - yA) < 0.0) {//A,B,P与方位角增加方向相反 A = -A; B = -B; sign = -1.0; } double cA = 1.0 / tan(A); double cB = 1.0 / tan(B); double XP = (xA * cB + xB * cA + (yA - yB) * sign) / (cA + cB); double YP = (yA * cB + yB * cA + (xB - xA) * sign) / (cA + cB); double deltaX = XP - xP; double deltaY = YP - yP; |
验证方法:deltaX和deltaY应该接近于零。
1.2 方位前方交会
 1.2.1 公式推导
1.2.1 公式推导

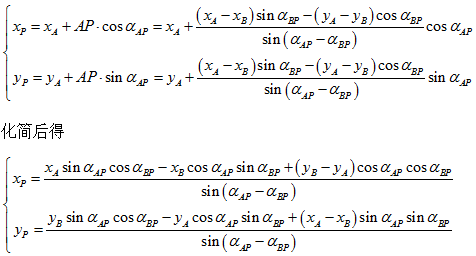
1.2.2 验证代码
验证上面公式的C代码如下:
|
srand(time(NULL)); double xA = rand(); double yA = rand(); double xB = rand(); double yB = rand(); double xP = rand(); double yP = rand(); double aAP = atan2(yP - yA,xP - xA); double aBP = atan2(yP - yB,xP - xB); double ca = cos(aAP); double sa = sin(aAP); double cb = cos(aBP); double sb = sin(aBP); double sab = sa * cb - ca * sb; //sin(aAP - aBP); double XP = (xA*sa*cb - xB*ca*sb + (yB - yA)*ca*cb) / sab; double YP = (yB*sa*cb - yA*ca*sb + (xA - xB)*sa*sb) / sab; double deltaX = XP - xP; double deltaY = YP - yP; |
验证方法:deltaX和deltaY应该接近于零。
第2章精度评定