DFS(深度优先)与BFS(广度优先)是两种非常重要的算法,要注意的是,这是算法,与其数据结构并无关系,任何数据结构都可以使用这种算法!其中树和图的数据结构使用该算法比较多。
这两种算法原理非常好理解,但是他们的应用极其的灵活,而且实现步骤上极其讲究,非常容易编写错误,但又找不到问题的出处,希望这两篇文章可以从原理到实现,从实现到应用完整的讲解DFS与BFS
这篇文章为对DFS的整理,文末为Leetcode相关习题讲解:
什么是DFS?说白了就是一直遍历元素的方式而已,我们可以把它看成是一条小蛇,在每个分叉路口随意选择一条路线走,直到撞到南墙,才会调头返回到上一个分叉路口,走另外一条路,有时候运气很好,撞到了目标点,那么这个算法就结束了。
说实话,我总感觉DFS是一种撞大运的算法,每次想到那条迷路的蛇撞来撞去,就觉得很好笑。
手动模拟一下它的路径:
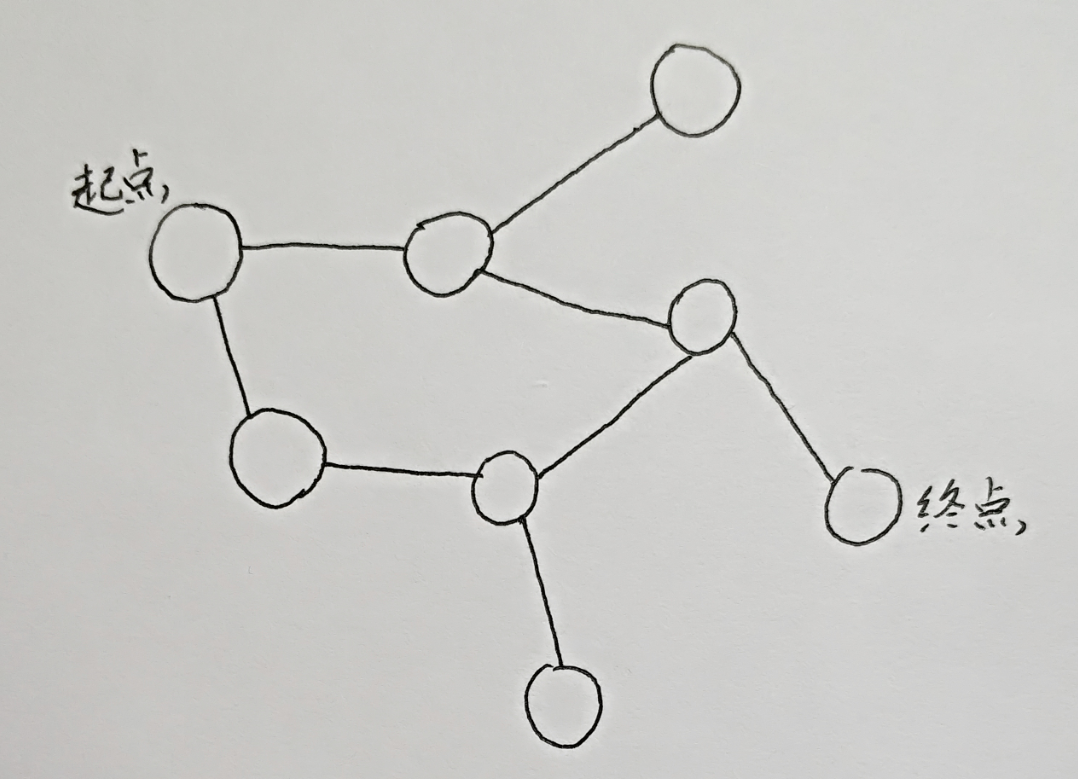
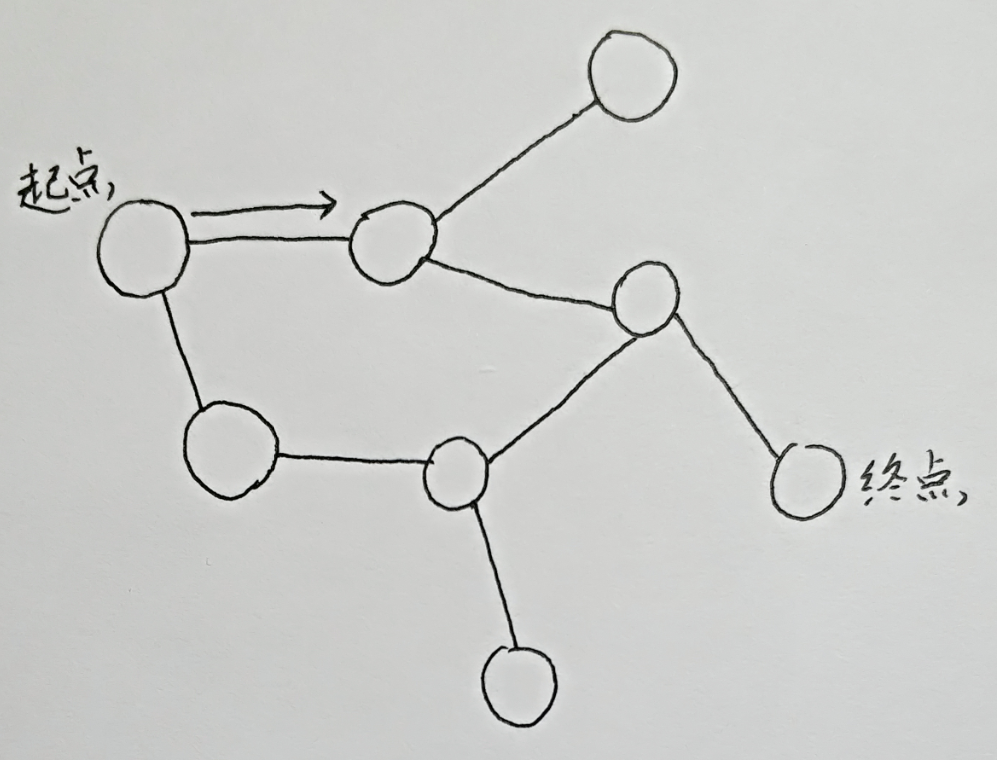
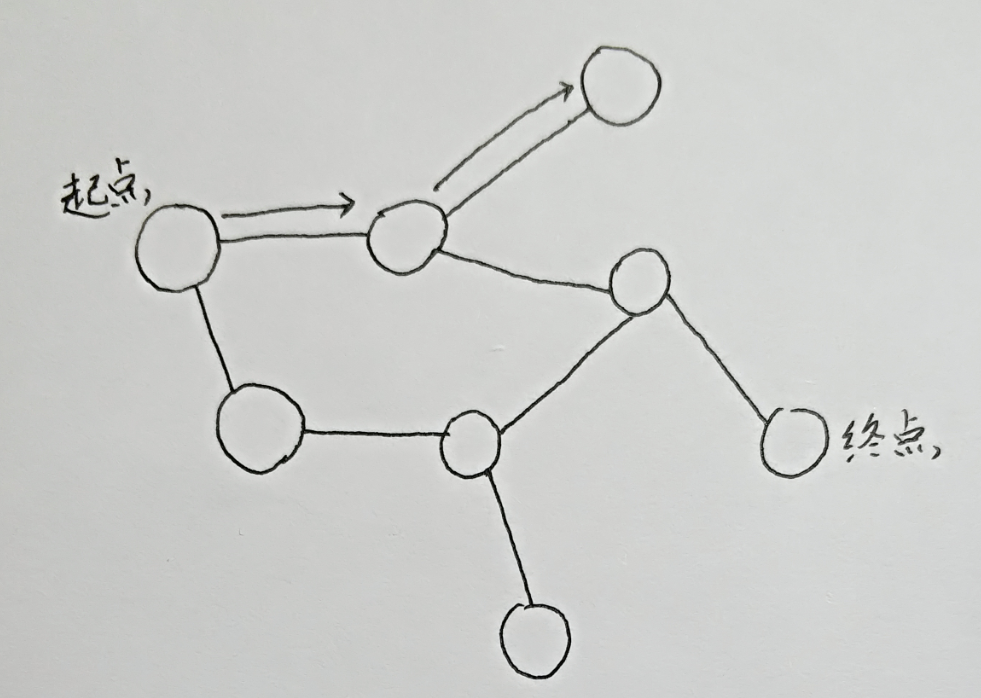
遇到南墙要返回

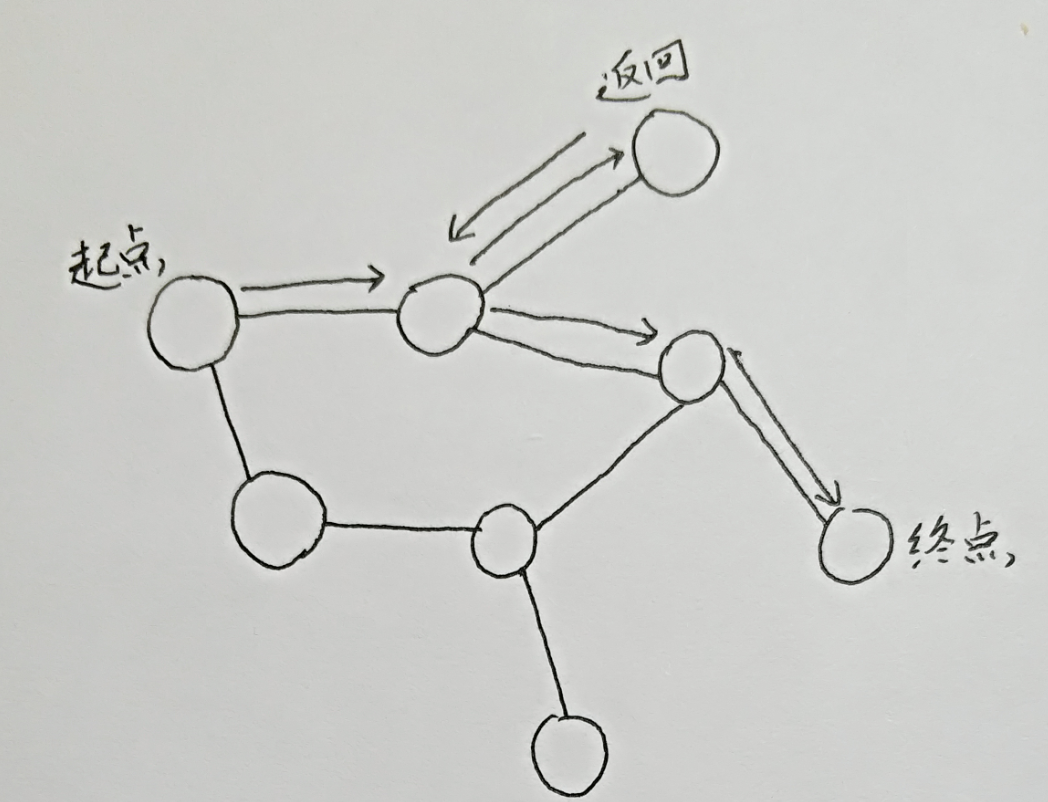
这便是DFS的最基础的原理。
应该如何来实现它呢?
DFS一般有两种实现方法:栈和递归
其实递归便是应用了栈的思想,而一般递归的写法非常简单,因为在刷题中编写简单还是比较重要的,所以我主要讲解递归的写法(Java实现)
以下为伪代码:
1 public 参数1 DFS(参数2)
2 {
3 if(返回条件成立) return 参数 ;
4 DFS(进行下一步的搜索遍历) ;
5 }
先分析if语句:
这句话的作用就是告诉小蛇:是否撞到南墙啦?撞到就返回啦,或者,是否到达终点啦?到了就结束啦!
所以我们在思考使用DFS进行解决问题的时候需要思考这两个问题:是否有条件不成立的信息(撞到南墙),是否有条件成立的信息(到达终点)。
还有一个非常重要的信息:是否需要标记访问节点。
下面来谈谈为什么要标记访问节点,以及如何来标记访问节点。
还是以刚才的路径为例:
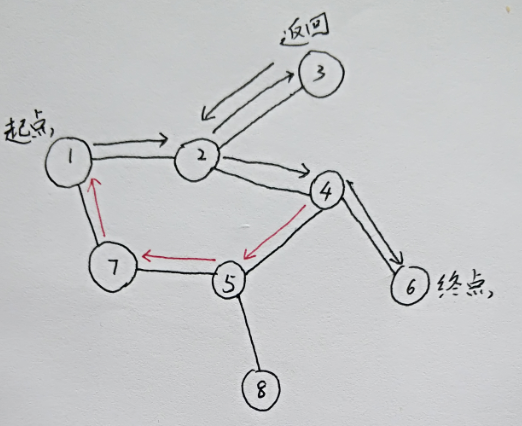
注意当我们的小蛇走到了4号节点时,没有选择去到6号节点,而是去到了5号节点,并沿红色路径行进,这样子是不是很有可能产生一个回环:
1->2->4->5->7->1,你会发现我们的小蛇在疯狂绕圈,肯定是到不了终点6号了。如何才能帮助我们的小蛇呢?
当然是通过标记路径了!
标记路径的原理是什么呢?
小蛇每走过一个节点便标记这个节点为已经访问,小蛇每次需要访问新节点时不会选择已经访问过的节点,这样就避免了出现回环的惨案。
如下图所示,红色的阴影表示已经访问过的节点,小蛇在7号节点时发现1号节点已经访问,所以只好返回,并标记7号节点为以访问。
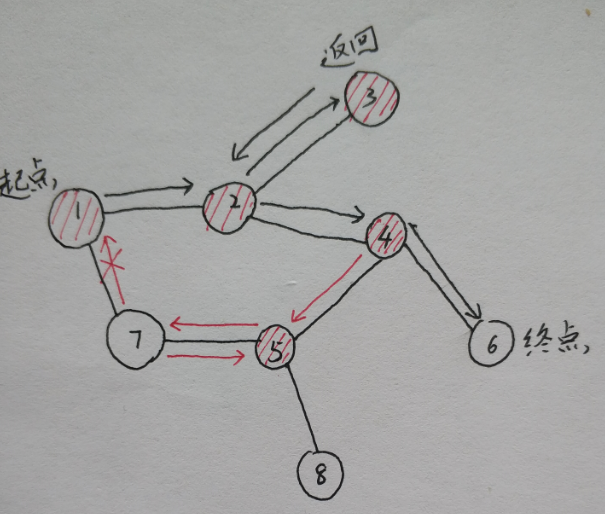
那么如何来标记一个节点是否访问过呢?
有超级多的方法来表示,常见的方法有数组法和HashSet法
boolean[] visited = new boolean[length] ; //数组表示,每访问过一个节点,数组将对应元素置为true Set<类型> set = new HashSet<>() ; //建立set,每访问一个节点,将该节点加入到set中去
总结一下,在第一部分,我们要思考3个问题
1,是否有条件不成立的信息(撞南墙)
2,是否有条件成立的信息(到终点)
3,是否需要记录节点(记轨迹)
下面,提一个小问题:如果我要遍历一个图中的所有节点,以上的3个问题如何回答?
答:
条件1:不成立的信息就是没有节点访问
条件2:没有条件成立的信息(没有终点)
条件3:需要记录轨迹
所以这个问题的解就是让小蛇没有新节点访问,便完成了整个图的遍历
——————————————————————————————————————————————————————————————————————
以上便是建立DFS的第一部分
下面来讨论DFS结构的第二部分——递归调用
先把总结构放上来:
public 参数1 DFS(参数2) { if(返回条件成立) return 参数 ; DFS(进行下一步的搜索遍历) ; }
递归调用的作用是什么?
在我看来,递归调用就像是一个方向盘,用来把控下一个节点应该访问哪里,是左边还是右边?是上还是下?在小蛇的例子中递归的作用就是告诉小蛇分叉路口应该选择哪个节点,所以DFS的参数为一些"方向"性质的参数。
同时递归还可以起到一个计数器的作用,可以记录每一条岔路的信息(可能我这么说有一些抽象,但在后面的题目中,我会进一步讲解),所以DFS的参数中也经常出现一些"记录"性质的参数。
————————————————————————————————————————————————————————
下面来看Leetcode上的题目
#1 Number of Islands
Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input:
11110
11010
11000
00000
Output: 1
Example 2:
Input:
11000
11000
00100
00011
Output: 3
1为陆地 ,0为水,陆地的左右上下都为0时,为一个岛,假定给定二维数组之外都是0(都是水),问给定一个二维数组确定有几个岛?
这是一个DFS应用于数组的典型例子,我们应用DFS将1相连的陆地遍历一遍,看一共需要遍历几次,便是几个岛屿
思考一下if语句的信息:
1.有无终止条件(撞南墙):当然有,当小蛇遇到水(0),超出数组边界(为水),就算是撞南墙了;
2.有无成立条件(到终点):这个没有,我们希望小蛇可以将这个岛遍历一遍;
3.是否需要记录轨迹:需要,防止小蛇重复,让小蛇不错过岛上的每一个土地(1);
那么我们再来想一想遍历的信息:
1."方向性"问题:小蛇需要左右上下来进行移动;
2."记录信息" :不需要,小蛇只管遍历就ok;
DFS代码如下:
public void dfs(int i , int j ,char[][] grid) //grid为输入的二维数组,i,j为小蛇的位置 { if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != '1') //“撞南墙” return ; grid[i][j] = '0' ; //记录节点轨迹,这里的记录方法非常巧妙,将访问之后的陆地变成水,小蛇自然不会再去访问了 dfs(i+1,j,grid); //递归调用,来控制小蛇的方向:左右上下 dfs(i-1,j,grid); dfs(i,j+1,grid); dfs(i,j-1,grid); }
所以在“主函数”中只需找到为“1”的陆地,然后调用DFS让它变成一片海,记录下来调用的次数便是有几个岛屿了
完整代码如下:
class Solution { public int numIslands(char[][] grid) { int res = 0 ; for(int i = 0 ; i < grid.length ; i ++) { for(int j = 0 ; j < grid[0].length ; j++) { if(grid[i][j] == '1') //找到为1的陆地,调用DFS使之变成大海 { res ++ ; //记录调用的次数 dfs(i,j,grid) ; } } } return res ; } public void dfs(int i , int j ,char[][] grid) { if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != '1') return ; grid[i][j] = '0' ; dfs(i+1,j,grid); dfs(i-1,j,grid); dfs(i,j+1,grid); dfs(i,j-1,grid); } }
#2 Clone Graph
Given the head of a graph, return a deep copy (clone) of the graph. Each node in the graph contains a label (int) and a list (List[UndirectedGraphNode]) of its neighbors. There is an edge between the given node and each of the nodes in its neighbors.
OJ's undirected graph serialization (so you can understand error output):
Nodes are labeled uniquely.
We use# as a separator for each node, and , as a separator for node label and each neighbor of the node.
As an example, consider the serialized graph {0,1,2#1,2#2,2}.
The graph has a total of three nodes, and therefore contains three parts as separated by #.
- First node is labeled as
0. Connect node0to both nodes1and2. - Second node is labeled as
1. Connect node1to node2. - Third node is labeled as
2. Connect node2to node2(itself), thus forming a self-cycle.
Visually, the graph looks like the following:

1.有无终止条件(撞南墙):当然有,遇到一个节点没有新的节点可以访问了;
2.有无成立条件(到终点):这个没有,我们希望可以将图上的所有节点遍历一遍;
3.是否需要记录轨迹:需要,我们每次只遍历新的节点 ;
递归:
1.方向是新节点的方向
2.不需要记录信息
但这些只解决了图上的所有节点的复制问题,对于每个节点的邻节点却无法完整复制,所以我们在DFS的同时还要将节点的邻接点也复制上,代码如下:
public void dfs(HashMap<UndirectedGraphNode,UndirectedGraphNode> hm , UndirectedGraphNode node) { if(node == null) return ; for(UndirectedGraphNode aneighbor : node.neighbors) //遍历给定节点的邻接点 { if(!hm.containsKey(aneighbor)) //如果为一个新的邻接点(还没有复制) { UndirectedGraphNode nd = new UndirectedGraphNode(aneighbor.label); //复制其节点 hm.put(aneighbor,nd); //新节点与原节点进行映射 dfs(hm,aneighbor); //递归新的节点,千万注意dfs的位置,在这里调用是有记录的,方向为新节点方向 } hm.get(node).neighbors.add(hm.get(aneighbor)); //复制其邻接点 } }
在“主函数”中主要是建立原头节点与新头节点的映射,全部代码如下:
/**
* Definition for undirected graph.
* class UndirectedGraphNode {
* int label;
* List<UndirectedGraphNode> neighbors;
* UndirectedGraphNode(int x) { label = x; neighbors = new ArrayList<UndirectedGraphNode>(); }
* };
*/
public class Solution { public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) { if(node == null) return null ; HashMap<UndirectedGraphNode,UndirectedGraphNode> hm = new HashMap<UndirectedGraphNode,UndirectedGraphNode>(); UndirectedGraphNode head = new UndirectedGraphNode(node.label); hm.put(node,head); dfs(hm,node); return head ; } public void dfs(HashMap<UndirectedGraphNode,UndirectedGraphNode> hm , UndirectedGraphNode node) { if(node == null) return ; for(UndirectedGraphNode aneighbor : node.neighbors) { if(!hm.containsKey(aneighbor)) { UndirectedGraphNode nd = new UndirectedGraphNode(aneighbor.label); hm.put(aneighbor,nd); dfs(hm,aneighbor); } hm.get(node).neighbors.add(hm.get(aneighbor)); } } }
#3 Target Sum
You are given a list of non-negative integers, a1, a2, ..., an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.
Find out how many ways to assign symbols to make sum of integers equal to target S.
Example 1:
Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
There are 5 ways to assign symbols to make the sum of nums be target 3.
Note:
- The length of the given array is positive and will not exceed 20.
- The sum of elements in the given array will not exceed 1000.
- Your output answer is guaranteed to be fitted in a 32-bit integer.
题目大意:>_< 大家自己查一下吧。。。不想翻译了。。。主要是我也翻译的不清楚。。。
你可能会很奇怪,这是一个一维的数组,怎么还可以DFS呀?
对,这就是DFS的灵活与巧妙之处,正如我文章开头所说,DFS是一种算法,或者说是一种思想,和数据结构没有任何关系,一定要搞清楚数据结构与算法的关系。
重要能够在问题中找到DFS中的那几个问题的答案,就可以应用DFS
还是那3个条件,2个递归:
条件1:是否出现“撞南墙” :出现了,当递归次数等于数组大小时,“撞南墙”不可以继续递归了
条件2:是否存在“终点” :存在,当“撞南墙”的时候,累加的结果刚好等于给定的结果时,到达终点
条件3:是否需要记录轨迹:这是一个一维数组啊,没有回环,所以不需要记录
递归:
1.“方向”:两个方向:“ + ” 或者 “ - ”
2.是否需要记录信息:需要记录,记录每次递归之后和的值
所以DFS代码如下:
public void dfs(int[] nums , int s , int sum , int k) //s为目标的数值 ,sum是记录每次递归之后的和的值 { if(k == nums.length) { if(sum == s) { res ++ ;//每次成功后记录成功次数 } return ; } dfs(nums,s,sum + nums[k],k+1) ; //递归方向 dfs(nums,s,sum - nums[k],k+1) ; }
总代码如下:
class Solution { int res = 0 ; public int findTargetSumWays(int[] nums, int S) { if(nums == null) return 0 ; dfs(nums,S,0,0); return res ; } public void dfs(int[] nums , int s , int sum , int k) { if(k == nums.length) { if(sum == s) { res ++ ; } return ; } dfs(nums,s,sum + nums[k],k+1) ; dfs(nums,s,sum - nums[k],k+1) ; } }
#4 树的遍历
树的遍历也可以使用DFS,这是一种极为简便的调用方式,一下给出树的结构,以及3种遍历方式的代码,大家自行分析那5个问题分别是什么
//二叉树节点 public class BinaryTreeNode { private int data; private BinaryTreeNode left; private BinaryTreeNode right; public BinaryTreeNode() {} public BinaryTreeNode(int data, BinaryTreeNode left, BinaryTreeNode right) { super(); this.data = data; this.left = left; this.right = right; } public int getData() { return data; } public void setData(int data) { this.data = data; } public BinaryTreeNode getLeft() { return left; } public void setLeft(BinaryTreeNode left) { this.left = left; } public BinaryTreeNode getRight() { return right; } public void setRight(BinaryTreeNode right) { this.right = right; } }
//前序遍历递归的方式 public void preOrder(BinaryTreeNode root){ if(null!=root){ System.out.print(root.getData()+" "); preOrder(root.getLeft()); preOrder(root.getRight()); } } //中序遍历采用递归的方式 public void inOrder(BinaryTreeNode root){ if(null!=root){ inOrder(root.getLeft()); System.out.print(root.getData()+" "); inOrder(root.getRight()); } } //后序遍历采用递归的方式 public void postOrder(BinaryTreeNode root){ if(root!=null){ postOrder(root.getLeft()); postOrder(root.getRight()); System.out.print(root.getData()+" "); } }
最后来一道比较困难的题目:
#5 Evaluate Division
Equations are given in the format A / B = k, where A and B are variables represented as strings, and k is a real number (floating point number). Given some queries, return the answers. If the answer does not exist, return -1.0.
Example:
Given a / b = 2.0, b / c = 3.0.
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? .
return [6.0, 0.5, -1.0, 1.0, -1.0 ].
The input is: vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries , where equations.size() == values.size(), and the values are positive. This represents the equations. Return vector<double>.
According to the example above:
equations = [ ["a", "b"], ["b", "c"] ], values = [2.0, 3.0], queries = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ].
The input is always valid. You may assume that evaluating the queries will result in no division by zero and there is no contradiction
题干比较长,大家可以找一下相关的翻译,我就不翻译了哈。
这道题目有两个比较难的点:1.构造图的结构,2.DFS的寻找路径
首先来讲解一下如何来构造图的结构。
我们根据题目的案例可以画出如下的图:
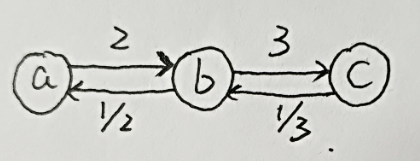
已知 a/b = 2 , b/c = 3 ,所以可以得知a->b为2 ,b->c为3,同理 b/a 为 1/2 , c/b为1/3 ,所以如果我们想求a/c,只需将a->b->c路径上的权值乘起来就ok 2*3=6,同理求c/a 则将c->b->a上的权值相乘就好,由此我们将这个问题转化成了寻找两点之间最短路径的问题,具体构造图的代码如下:(具体如何构建图,以后会在数据结构中进行总结,本篇文章重点为DFS)
public double[] calcEquation(String[][] equations, double[] values, String[][] queries) { double[] num = new double[queries.length] ; Map<String,List<Adam>> map = new HashMap<>(); for(int i = 0 ; i < equations.length ; i ++) { if(!map.containsKey(equations[i][0])) map.put(equations[i][0],new ArrayList<>()); map.get(equations[i][0]).add(new Adam(equations[i][1],values[i])) ; if(!map.containsKey(equations[i][1])) map.put(equations[i][1],new ArrayList<>()); map.get(equations[i][1]).add(new Adam(equations[i][0],1/values[i])) ; } } class Adam { String s ; double dis ; Adam(String s , double dis) { this.s = s ; this.dis = dis ; } }
将图建立好之后,只需要将案例中的queries两两加入到DFS中寻找路径上的乘积结果就好
for(int i = 0 ; i < queries.length ; i ++) { num[i] = findPath(queries[i][0],queries[i][1],1.0,new HashSet()) ; }
下面我们来讨论DFS
还是那3个条件,2个迭代:
1.有“南墙”吗:有,节点上没有还未访问的节点时,图中没有对应节点时,出现自环时“撞南墙”。
2.有“终点”吗:有,当寻找到终点节点时“成功”。
3.需要记录访问节点吗:需要的,防止出现“回环。”
迭代:
1.“方向”是什么:为还没有访问过的节点。
2.需要记录迭代信息吗:需要,要记录每次迭代路径相乘的结果。
代码如下:
public double findPath(String start ,String end , double val,Set<String> visited) //这里我们使用hashset来记录路径 { if(visited.contains(start)) return -1.0 ; //自环出现,“南墙” || 访问过该节点 if(!map.containsKey(start)) return -1.0 ; //图中没有相应节点 if(start.equals(end)) return val ; //成功的标志———找到终点 visited.add(start) ; //记录路径 for(Adam next : map.get(start)) { //遍历每个节点 double sub = findPath(next.s, end, val* next.dis, visited); if(sub != -1.0) return sub; } return -1.0 ; }
完整代码如下:
class Solution { Map<String,List<Adam>> map = new HashMap<>(); public double[] calcEquation(String[][] equations, double[] values, String[][] queries) { double[] num = new double[queries.length] ; //Set<String> visited = new HashSet<>() ; 要注意啊!!!!! for(int i = 0 ; i < equations.length ; i ++) { if(!map.containsKey(equations[i][0])) map.put(equations[i][0],new ArrayList<>()); map.get(equations[i][0]).add(new Adam(equations[i][1],values[i])) ; if(!map.containsKey(equations[i][1])) map.put(equations[i][1],new ArrayList<>()); map.get(equations[i][1]).add(new Adam(equations[i][0],1/values[i])) ; } for(int i = 0 ; i < queries.length ; i ++) { num[i] = findPath(queries[i][0],queries[i][1],1.0,new HashSet()) ; //注意,每次寻找新的路径时需要新建一个hashset } return num ; } public double findPath(String start ,String end , double val,Set<String> visited) { if(visited.contains(start)) return -1.0 ; if(!map.containsKey(start)) return -1.0 ; if(start.equals(end)) return val ; visited.add(start) ; for(Adam next : map.get(start)) { double sub = findPath(next.s, end, val* next.dis, visited); if(sub != -1.0) return sub; } return -1.0 ; } class Adam { String s ; double dis ; Adam(String s , double dis) { this.s = s ; this.dis = dis ; } } }
这里有一点非常值得注意(代码中以标出),每次寻找路径时需要新建一个hashset ,这样清空节点的标记,方便重新寻找新路径。
—————————————————————————————————————————————————————————
总结:
我们什么时候应该使用DFS呢?
当我们遇到的问题与路径相关,且不是寻找最短路径(最短路径为BFS,下次再说),或者需要遍历一个集合中的所有元素,或者是查找某一种问题的全部情况时,我们可以考虑使用DFS来求解。
更重要的是,要将数据结构的概念与算法分离开,才可以将算法灵活运用。