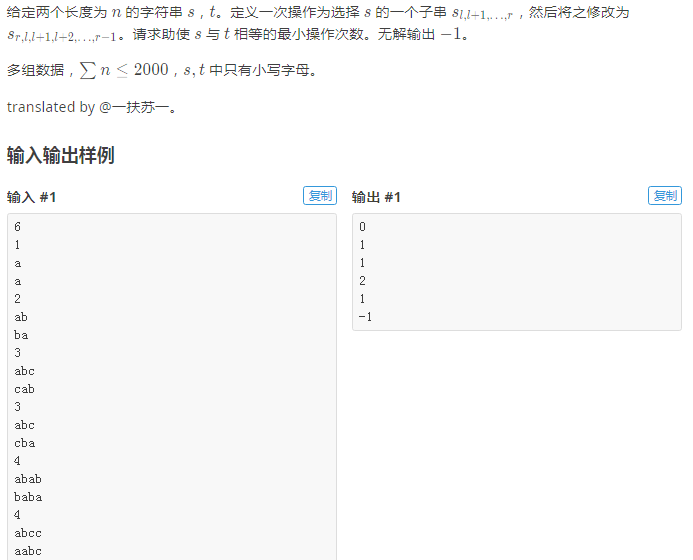
题解:
$nleq 2000$ ,考虑$O(n^2)$的算法
n^2的解决字符串问题大概率要使用Dp,由于要进行两个字符串的匹配,那么我们试图设$dp[i][j]$表示s串的前i位与t串的前j位匹配的最小代价
怎么进行状态转移?
胡乱搞一搞
规定$i < j$,由于一次操作是把一个数扔到一个数的前面
所以$dp[i][j]=dp[i-1][j]+1$(如果第i个位置与$t_1$~$t_j$都不匹配,那么最优解应该是将这个字符后面的字符都往前扔,而不对他进行操作,所以这种情况出现时这种状态一定不会转移到最终的最优解中)
然后如果s[i]=t[j],那么dp[i][j]也可以通过dp[i-1][j-1]转移过来
当t[j]是从i后面扔过来的时候dp[i][j]=dp[i][j-1]而这一次扔过来的代价将会在第一种转移中计算
但是为了能转移到第一种状态,那么一定要保证这个数一定是后面匹配时富余出来的
然后就结束了