众所周知,斜率优化$DP$是很(mei)优(luan)秀(yong)的算法。
所以,就和博主一起来学习吧。
例题一:任务安排
【题目描述】
有$N$个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。机器会把这$N$个任务分成若干批,每一批包含连续的若干个任务。从时刻$0$开始,任务被分批加工,执行第$i$个任务所需的时间是$T_{i}$。另外,在每批任务开始前,机器需要$S$的启动时间,故执行一批任务所需的时间是启动时间$S$加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。也就是说,同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数$C_{i}$。
请为机器规划一个分组方案,使得总费用最小。
【分析】通过题目描述,我们可以很轻松的看出这是一个$DP$题目。
我们设$sumc[i]$表示费用的前缀和,$sumt[i]$表示时间的前缀和。
所以我们可以列出$DP$方程:
$$dp[i]=min(dp[i],sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j])+dp[j])$$
但是,这个$DP$转移是$n^2$的,在$3 imes10^5$次方的数据范围下会T到天上。
于是,我们考虑将$DP$方程化简:
$$dp[i]=dp[j]-(s+sumt[i])*sumc[j]+sumt[i]*sumc[i]+s*sumc[n]$$
看到这个式子,依然没有什么头绪,所以我们可以找到两个决策点k,j,假设k优于j,则
$$dp[j]-(s+sumt[i])*sumc[j]+sumt[i]*sumc[i]+s*sumc[n]geq dp[k]-(s+sumt[i])*sumc[k]+sumt[i]*sumc[i]+s*sumc[n]$$
继续整理式子
$$dp[j]-(s+sumt[i])*sumc[j]geq dp[k]-(s+sumt[i])*sumc[k]$$
$$dp[j]-dp[k] geq s*sumc[j]-sumt[i]*sumc[j]-s*sumc[k]+sumt[i]*sumc[k]$$
$$dp[j]-dp[k] geq (s+sumt[i])*(sumc[j]-sumc[k])$$
$$frac{dp[j]-dp[k]}{(sumc[j]-sumc[k])} geq (s+sumt[i])$$
可以发现,左边的式子是形如$frac{Y_{1}-Y_{2}}{X_{1}-X_{2}}$的式子,而右边的式子是一个常量。
我们可以想到斜率!构建一个平面直角坐标系,以$sumc[i]$为横坐标,以$dp[i]$为纵坐标:
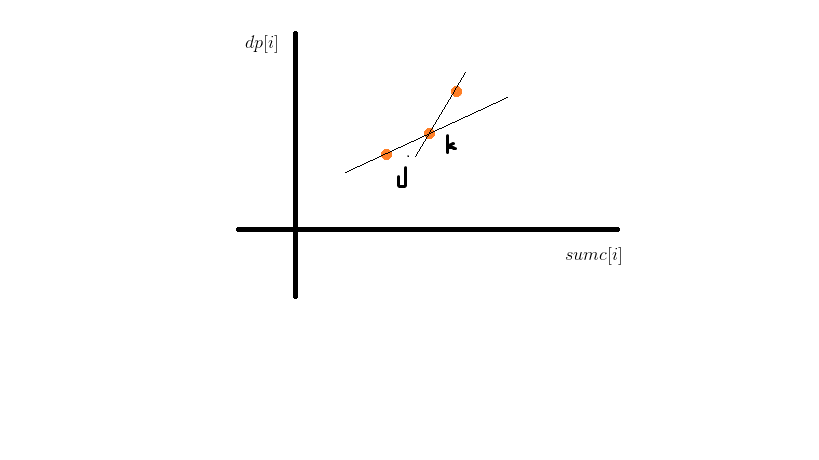
根据刚刚推出的$DP$,决策点k所在的直线的斜率只有大于它之前所有的点,小于它之后所有点的斜率,它才能被选中成为一个最优解。因为若k点最优,则应满足k点所在直线的截距是所有点中最小的。所以,这个k点应处于一个“下凸壳”的顶点处。因为在所有可能成为最优决策的点集中,点的编号与直线斜率都是递增的。根据这个性质,我们可以用单调队列来维护可能成为最优决策的点集。当单调队列头的两个点组成直线的斜率比当前直线的斜率$leq s+sumt[i]$小的时候,就将其弹出。当单调队列尾的两个点与当前点组成的不是“下凸壳”时,就将其弹出。
总结一下:当$DP$方程有a[i]*b[j]的项时:
①设决策点k优于j,化简方程,看是否能化简成不等式左边为形如$frac{Y_{1}-Y_{2}}{X_{1}-X_{2}}$,右边为一个常数的形式,若不能,则采用暴力;
②看这道题是维护上凸壳还是下凸壳。
下面给出任务安排的代码:

#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<deque> using namespace std; int sumt[300001],sumc[300001]; int dp[300001],q[300001]; int X(int i){return sumc[i];} int Y(int i){return dp[i];} int slope(int i,int j){return (Y(i)-Y(j))/(X(i)-X(j));} int main() { int n,s; scanf("%d%d",&n,&s); int i,j; for(i=1;i<=n;i++) { int c,t; scanf("%d%d",&t,&c); sumt[i]=sumt[i-1]+t; sumc[i]=sumc[i-1]+c; } int l=1,r=1; memset(dp,0x3f,sizeof(dp)); dp[0]=0; for(i=1;i<=n;i++) { while(l<r&&slope(q[l+1],q[l])<(sumt[i]+s)) l++; dp[i]=dp[q[l]]-(s+sumt[i])*sumc[q[l]]+sumt[i]*sumc[i]+s*sumc[n]; while(l<r&&slope(i,q[r])<slope(q[r],q[r-1])) r--; q[++r]=i; } cout<<dp[n]; }
既然学会了方法,那么接下来的事情就是刷题了。
【例题1】任务安排升级版 link
这题和上题一模一样,但是$sumc[i]$有可能是负的。所以下凸壳的性质就不能用了,我们就不能使用上一问的单调队列,所以需要二分遍历整个点集。
【例题2】Cats Transport link
这题思维难度较大,但是$DP$方程很简短。我们将饲养员正好接到猫的时间预处理,然后将其从小到大排序。我们设$dp[i][j]$表示前$i$个饲养员接前$j$只猫的时间。因为一个人接到第j只猫时,可以接到前面所有猫。所以我们枚举断点,可以列出$DP$方程:$dp[i][j]=min(dp[i][j],dp[i-1][x]+(j-x)*a[j]-sum[j])$,其中$a_{i}$表示正好接到第$i$只猫的出发时间,$sum[i]$表示$a[i]$的前缀和。
【例题3】玩具装箱 link
这题思维难度很小,但是式子的化简十分复杂。我们把$j-i$设为a,$sum[k]-sum[i]$设为$suma$,$sum[j]-sum[i]$设为$sumb$,采用换元的思想降低化简难度。最终化简出$X=sum[i]+i+L+1$,$Y=dp[i]+(sum[i]+i+L+1)^2$。
【例题四】仓库选址 link
很普通的一道斜率优化,dp方程留给大家自己推吧。
大家还可以试试2009年的江苏省选火星藏宝图,很好的思维题目。
蒟蒻第一次写博客,若写的不好请见谅~如果您发现有错误,请在评论区指出。
