Java实验--课上提到的随机数生成原理简单实现(不利用库生成随机数的简单算法）

对于随机数的实验，根据课程上的教程，有如下的公式：

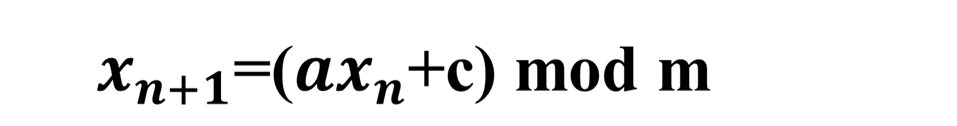
对应的变量参数的说明：

其中对应的Mouduls变量对应的就是公式中a的值，在公式中的含义就是相当于要循环多少个数才重复的一个值。

Multiplier对应的就是公式中m的值，表示的是范围值，例如图上的16807表示的就是取种子返回的随机数的范围为0-16806。

公式中的c表示的是公式每次返回的随机数要增长的一个值，如果是常数的话，每次增长的值将会是一个固定的值，就变成了容易重复的状态，所以，为了不使其是一个重复的状态，我打算在每次取完随机数之后将生成的随机数Xn赋值给c；

Xn表示的随机数函数中取种子的一个步骤，其中第一次取值，其实就是取种子的过程，也就是对X0取值的过程，当取到第一个种子后，此后的随机数一般都不用取种子了。

根据上述的简单分析，那么以下就是实验实现随机数的一个算法，代码如下：

package suijishu;

public class Suijishu {

    private long xn=0;
    private long c=0;
    public int random_num(int a,int b)
    {
        return (int) (random()%(b-a+1)+a);
    }
    public long random()    //生成第n+1个的随机数过程
    {
        int Multiplier=16807;
        long Modulus=((1<<31)-1);
        xn=(Modulus*xn+c)%Multiplier;
        c=xn;
        return xn;
    }
    public void setseed(long seed)    //取种子
    {
        xn=seed;
    }
    
    //主函数
    public static void main(String[] args) {
        // TODO 自动生成的方法存根
        Suijishu sjs=new Suijishu();
        int num[]=new int[6];    //模拟色子的六个面整型变量
        int account=0;
        sjs.setseed(System.currentTimeMillis());
        for(int i=0;i<6000;i++)    //模拟循环6000次摇色子的过程
        {
            account=sjs.random_num(1,6); //摇色子
            ++num[account-1];    //对应的色子面的变量加一
        }
        for(int j=0;j<6;j++)
        {
            System.out.println((j+1)+":"+num[j]);//看最终色子对应面被摇的次数
        }
    }
    
    
}

类中setseed是一个取种子的函数，我在代码中取的种子是系统的当前时间。（距离1970年1月1日的毫秒数），因为时间是一直在变得，因此取时间作为种子是一个不错的选择。

random()是一个取种子之后的返回随机数的函数

random_num(int a,int b)是一个封装的函数，返回a-b之间的随机数的值；

下面是实验的截图：

随机数的分布情况还是挺平均的。