0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
-
串的BF算法
-
- 从目标串s 的第一个字符起和模式串t的第一个字符进行比较,若相等,则继续逐个比较后续字符,否则就串s 的第二个字符起再重新和串t进行比较。
-
- 依此类推,直至串t 中的每个字符依次和串s的一个连续的字符序列相等,则称模式匹配成功,此时串t的第一个字符在串s 中的位置就是t 在s中的位置,否则模式匹配不成功。
代码
- 依此类推,直至串t 中的每个字符依次和串s的一个连续的字符序列相等,则称模式匹配成功,此时串t的第一个字符在串s 中的位置就是t 在s中的位置,否则模式匹配不成功。
{
if (pos <1 || pos > S[0] ) exit(ERROR);
int i = pos, j =1;
while (i<= S[0] && j <= T[0])
{
if (S[i] == T[j])
{
++i; ++j;
} else {
i = i- j+ 2;
j = 1;
}
}
if(j > T[0]) return i - T[0];
return ERROR;
}
- KMP算法
每当遍历出现字符比较不等时,不需要回到I指针,而是用“部分匹配”的结果将模式向右滑动尽可能远的一段距离后,继续进行比较。
代码实现
int KMPindex(SString S, SString T, int pos)
{
if (pos <1 || pos > S[0] ) exit(ERROR);
int i = pos, j =1;
while (i<= S[0] && j <= T[0])
{
if (S[i] == T[j]) {
++i; ++j;
} else {
j = next[j+1];
}
}
if(j > T[0]) return i - T[0];
return ERROR;
}
- 二叉树存储结构、建法、遍历及应用
二叉树存储结构
1 顺序存储结构
顺序存储一棵二叉树时,首先对该树中的每个结点进行编号,然后以各结点的编号为下标,把各结点的值对应存储到一个一位数组中。每个结点的编号与等深度的满二叉树中对应结点的编号相等,即树根结点的编号为1,接着按照从上到下和从左到右的次序,若一个结点的编号为i,则左、右孩子的编号分别为2i和2i+1。
2 链接存储结构
链接存储的方法是:在上面的结点结构中再增加一个parent指针域,用来指向其双亲结点。这种存储结构既便于查找孩子结点,也便于查找双亲结点,当然也带来存储空间的相应增加。
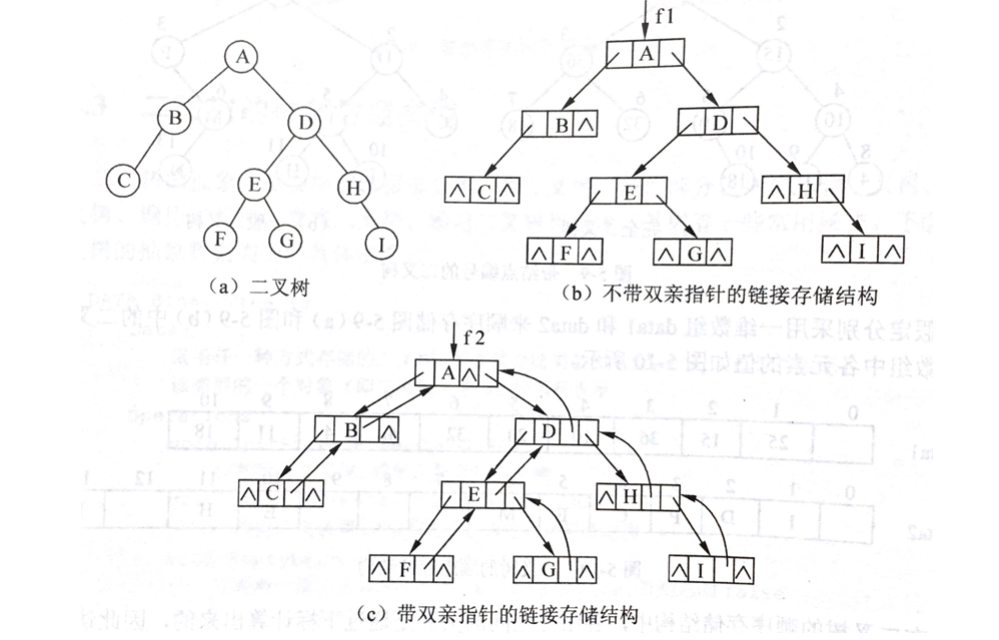
二叉树建法
递归法
void CreateBiTree(BiTree& T, char str[], int& i)
{
if (str[i] == '#')
T = NULL;
else
{
T = new BiTNode;
T->data = str[i];
CreateBiTree(T->lchild, str, ++i);
CreateBiTree(T->rchild, str, ++i);
}
}
二叉树遍历及应用
1.先序遍历
先序遍历的规则如下:若当前二叉树为空,则返回空,否则
- 访问根结点;
- 先序遍历左子树;
- 先序遍历右子树;
void PreorderPrintLeaves(BinTree BT)
{
if (BT)
{
if (!BT->Left && !BT->Right)
printf(" %c", BT->Data);
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
}
}
2.中序遍历
中序遍历的规则如下:若当前二叉树为空,则返回空,否则
- 中序列根结点的左子树;
- 访问根结点;
- 中序遍历根结点的右子树;
void PreorderPrintLeaves(BinTree BT)
{
if (BT)
{
if (!BT->Left && !BT->Right);
PreorderPrintLeaves(BT->Left);
printf(" %c", BT->Data);
PreorderPrintLeaves(BT->Right);
}
}
3.后序遍历
后序遍历的规则如下:若当前二叉树为空,则返回空,否则
- 后序列根结点的左子树;
- 后序遍历根结点的右子树;
- 访问根结点;
void PreorderPrintLeaves(BinTree BT)
{
if (BT)
{
if (!BT->Left && !BT->Right);
PreorderPrintLeaves(BT->Left);
PreorderPrintLeaves(BT->Right);
printf(" %c", BT->Data);
}
}
树的结构、操作、遍历及应用
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
char data;
struct node *l, *r;
}BinNode;
BinNode *create_tree() //创建树
{
BinNode *t;
char ch;
ch = getchar();
if(ch == '#') //#表示空
t = NULL;
else
{
t = (BinNode *)malloc(sizeof *t);
t->data = ch;
t->l = create_tree(); //递归创建左子树
t->r = create_tree(); //递归创建右子树
}
return t;
}
void pre_ord(BinNode *t) //先序遍历
{
if(t)
{
printf("%c", t->data);
pre_ord(t->l); //遍历左子树
pre_ord(t->r); //遍历左子树
}
}
void in_ord(BinNode *t) //中序遍历
{
if(t)
{
in_ord(t->l); //中序左子树遍历
printf("%c", t->data);
in_ord(t->r); //中序右子树遍历
}
}
void post_ord(BinNode *t) //后序遍历
{
if(t)
{
post_ord(t->l); //后序左子树遍历
post_ord(t->r); //后序右子树遍历
printf("%c", t->data);
}
}
void main()
{
BinNode *root = NULL;
root = create_tree();
printf("先序遍历:"); pre_ord(root); printf("
");
printf("中序遍历:"); in_ord(root); printf("
");
printf("后序遍历:"); post_ord(root); printf("
");
}
线索二叉树
利用原来的空链域存放指针,指向树中其他结点。这种指针称为线索。
记ptr指向二叉链表中的一个结点,以下是建立线索的规则:
(1)如果ptr->lchild为空,则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱;
(2)如果ptr->rchild为空,则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继;
显然,在决定lchild是指向左孩子还是前驱,rchild是指向右孩子还是后继,需要一个区分标志的。因此,我们在每个结点再增设两个标志域ltag和rtag,注意ltag和rtag只是区分0或1数字的布尔型变量,其占用内存空间要小于像lchild和rchild的指针变量。
void InThreading(BiTree p)
{
if(p)
{
InThreading(p->lchild); //递归左子树线索化
//===
if(!p->lchild) //没有左孩子
{
p->ltag = Thread; //前驱线索
p->lchild = pre; //左孩子指针指向前驱
}
if(!pre->rchild) //没有右孩子
{
pre->rtag = Thread; //后继线索
pre->rchild = p; //前驱右孩子指针指向后继(当前结点p)
}
pre = p;
//===
InThreading(p->rchild); //递归右子树线索化
}
}
其中:
(1)ltag为0时指向该结点的左孩子,为1时指向该结点的前驱;
(2)rtag为0时指向该结点的右孩子,为1时指向该结点的后继;
(3)因此对于上图的二叉链表图可以修改为下图的养子。
哈夫曼树
- 我们称判定过程最优的二叉树为哈夫曼树,又称最优二叉树
-路径: 树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
-路径长度:路径上的分枝数目称作路径长度。
-树的路径长度:从树根到每一个结点的路径长度之和。
-结点的带权路径长度:在一棵树中,如果其结点上附带有一个权值,通常把该结点的路径长度与该结点上的权值


1.2.谈谈你对树的认识及学习体会。
- 树确实在数据结构中占有很重要的地位,也是一个很难的点,需要有足够的耐心和精力去学习并理解,但在学习成功的时刻却会很自豪,
总之还是要好好的将数据结构这门难关给攻克了。
2.阅读代码
2.1 题目及解题代码

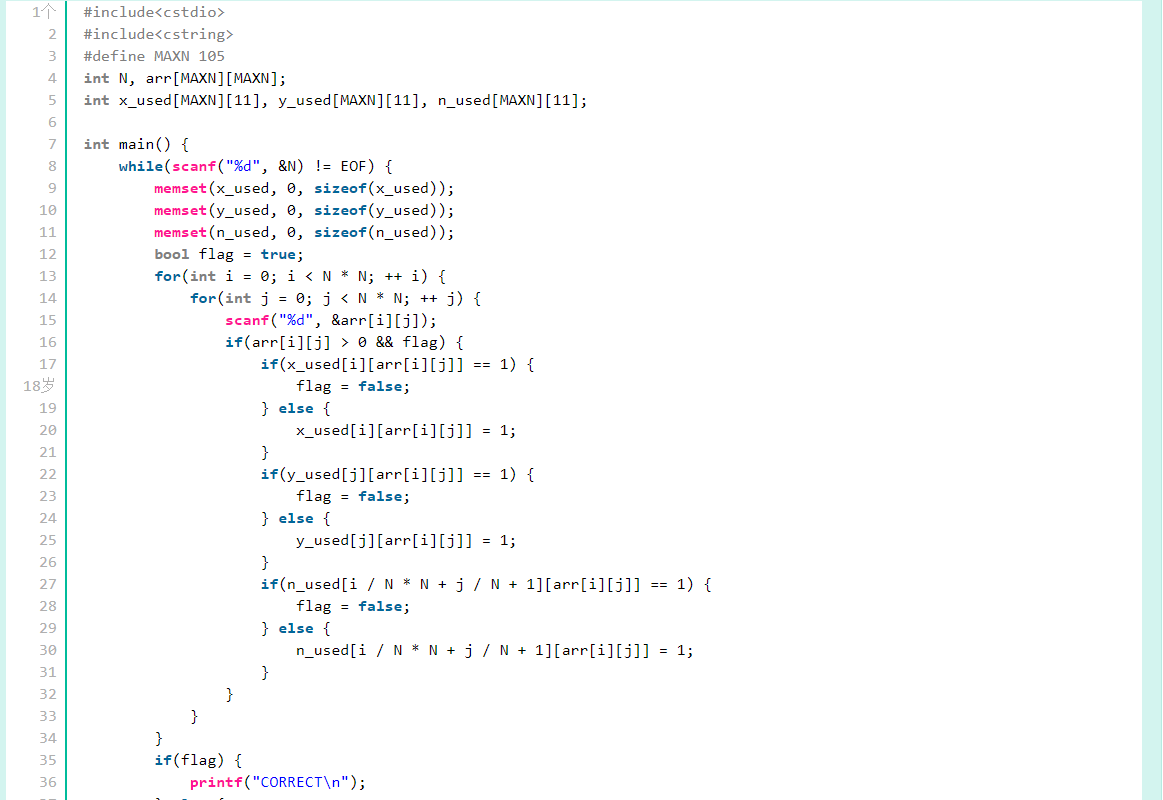

2.1.1 该题的设计思路
- 考察循环和多维数组的精确应用,通过数组来实现数独游戏的完成
2.1.3 运行结果
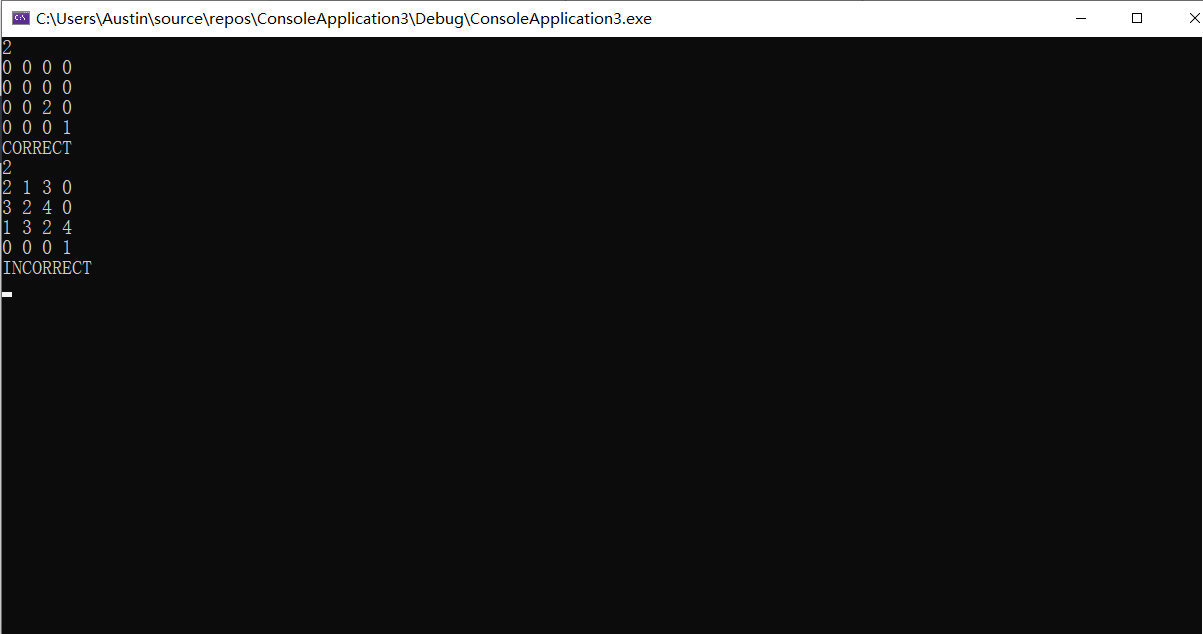
2.1.4分析该题目解题优势及难点。
- 此题的难点主要在于对数独功能的实际施行,如每行每列每斜行都不可有重复数字,对此的具体代码限制就显得有点困难,巧妙的运用多维数组可以很好的解决问题。