0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
- 栈的存储结构及操作

bool Push(Stack S, ElementType X)//入栈
{
if (S->Top >= S->MaxSize)
{
printf("Stack Full
");
return false;
}
else
{
S->Data[++(S->Top)]=X;
return X;
}
}
ElementType Pop(Stack S)//出栈
{
if (S->Top == 0)
{
printf("Stack Empty
");
return ERROR;
}
else
{
return (S->Data[(S->Top)--]);
}
}
- 栈的应用(判断表达式中的括号是否正确配对)
#include<iostream>
#include<stack>
using namespace std;
int main() {
string s;
cin >> s;
stack<char> st;
int flag = 1;
int flag1=0;
for (int i = 0; i < s.size(); i++)
{
if (s[i] == '(' || s[i] == '[' || s[i] == '{')
{
st.push(s[i]);
flag1=1;
}
else if (s[i] == ')' || s[i] == ']' || s[i] == '}')
{
if(st.empty())
{
cout<<"no";
return 0;
}
char temp = st.top();
st.pop();
if (!((s[i] == ')' && temp == '(') || (s[i] == ']' && temp == '[') || (s[i] == '}' && temp == '{')))
{
flag = 0;
cout << temp << endl << "no";
return 0;
}
}
}
if (st.empty())
{
cout << "yes";
}
else
{
cout << st.top() << endl << "no";
}
}
- 队列的存储结构及操作
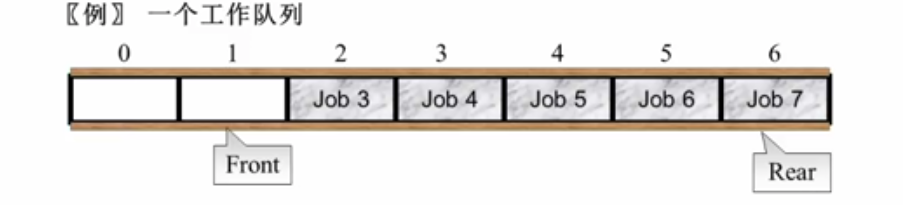
bool AddQ(Queue Q, ElementType X)//入队
{
if (Q->Count == Q->MaxSize)
{
printf("Queue Full
");
return false;
}
Q->Data[(Q->Count+1+Q->Front) % Q->MaxSize] = X;
Q->Count++;
}
ElementType DeleteQ(Queue Q)//出队
{
if (Q->Count == 0)
{
printf("Queue Empty
");
return ERROR;
}
Q->Count--;
Q->Front = (Q->Front + 1) % (Q->MaxSize);
return Q->Data[Q->Front];
}
- 队列应用(报数游戏)
while (s.size() != 0) {
for (int i = 1; i < m; i++)
{
if (it == s.end()) {
it = s.begin();
}
it++;
}
if (!(it != s.end()))
{
it = s.begin();
}
if (flag == 0)
{
cout << *it;
flag = 1;
}
else
{
cout <<" "<< *it;
}
int c = *it;
s.erase(c);
int j = 1;
while (1)
{
it = s.find((c + j) % n);
if (it != s.end())
break;
else
j++;
if(j==n)
{
break;
}
}
}
2.PTA实验作业
2.1符号配对
2.1.1代码截图
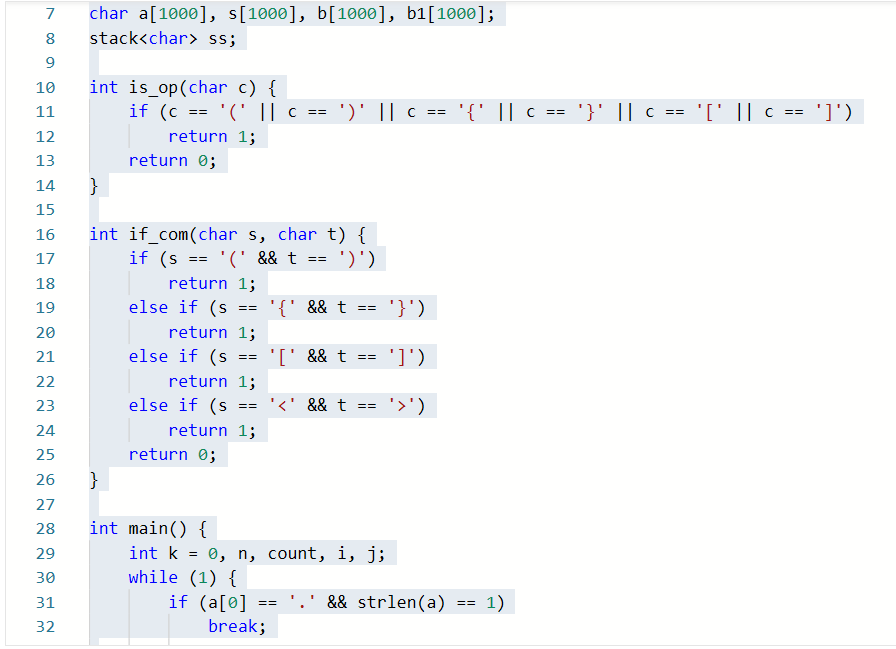
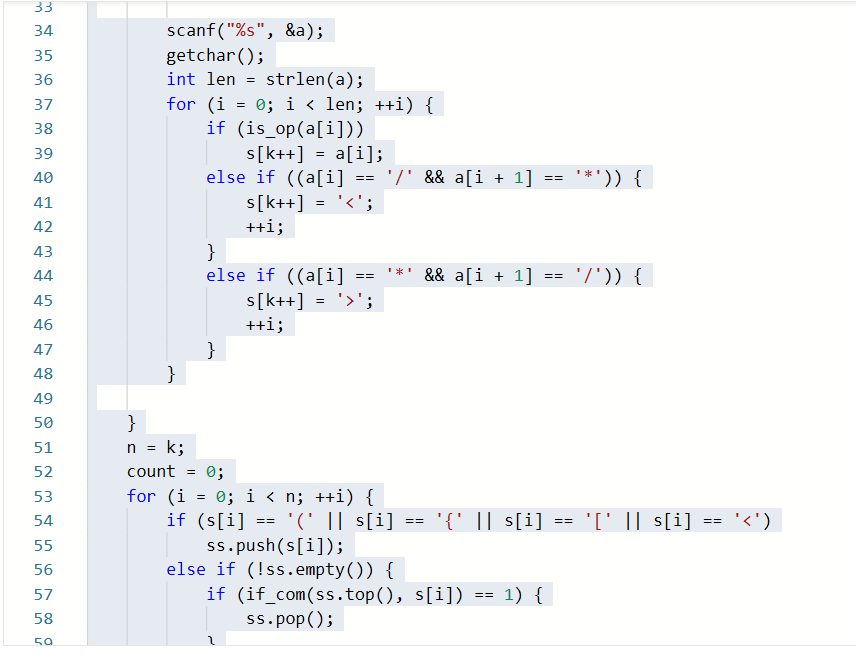
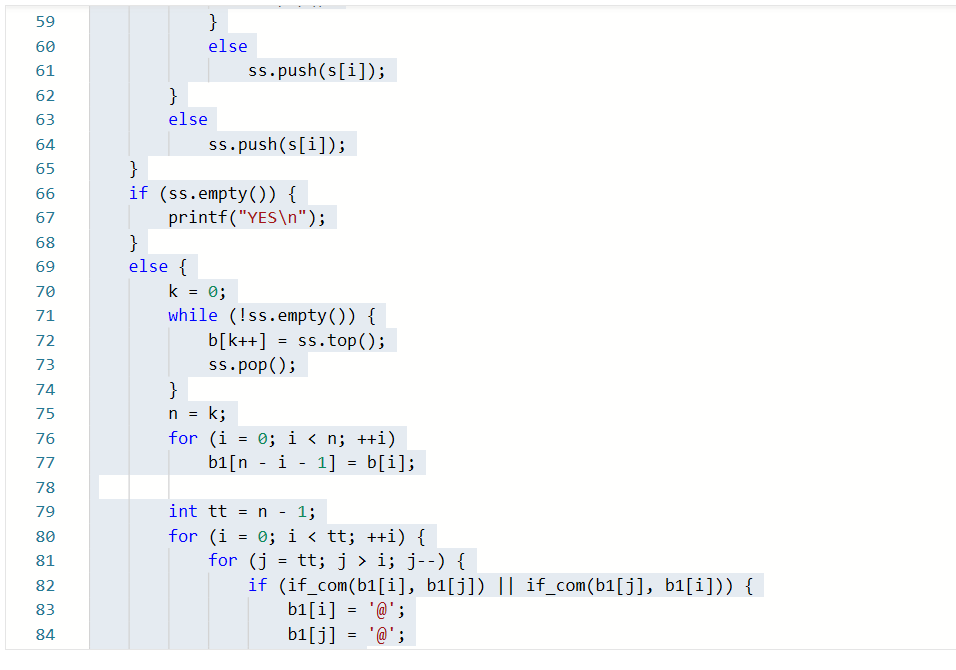
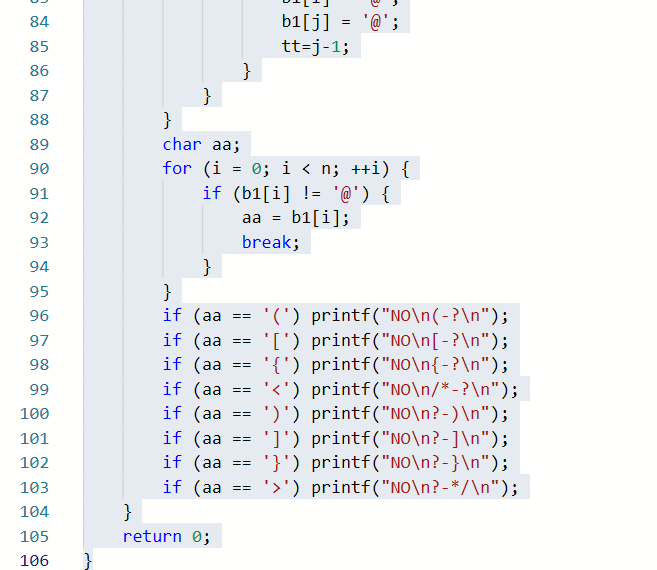
2.1.2本题PTA提交列表说明


一开始是因为编译器没选对,导致编译一直失败,因为此题老师讲过,所以问题不大。
2.2字符串是否对称
2.2.1代码截图
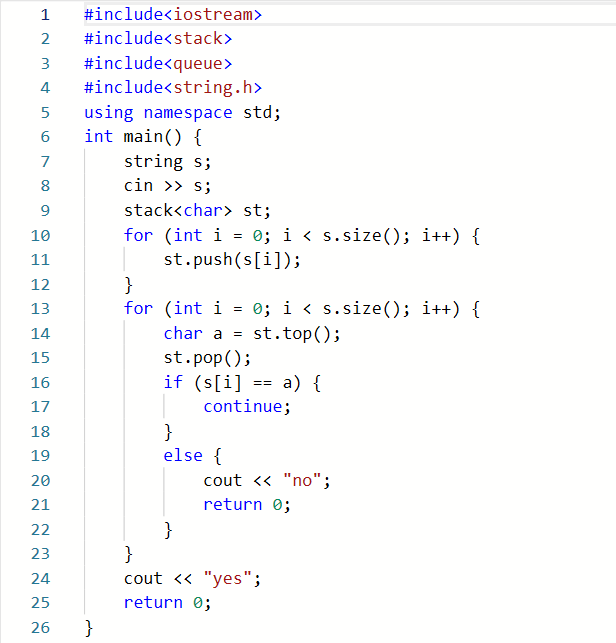
2.2.2本题PTA提交列表说明
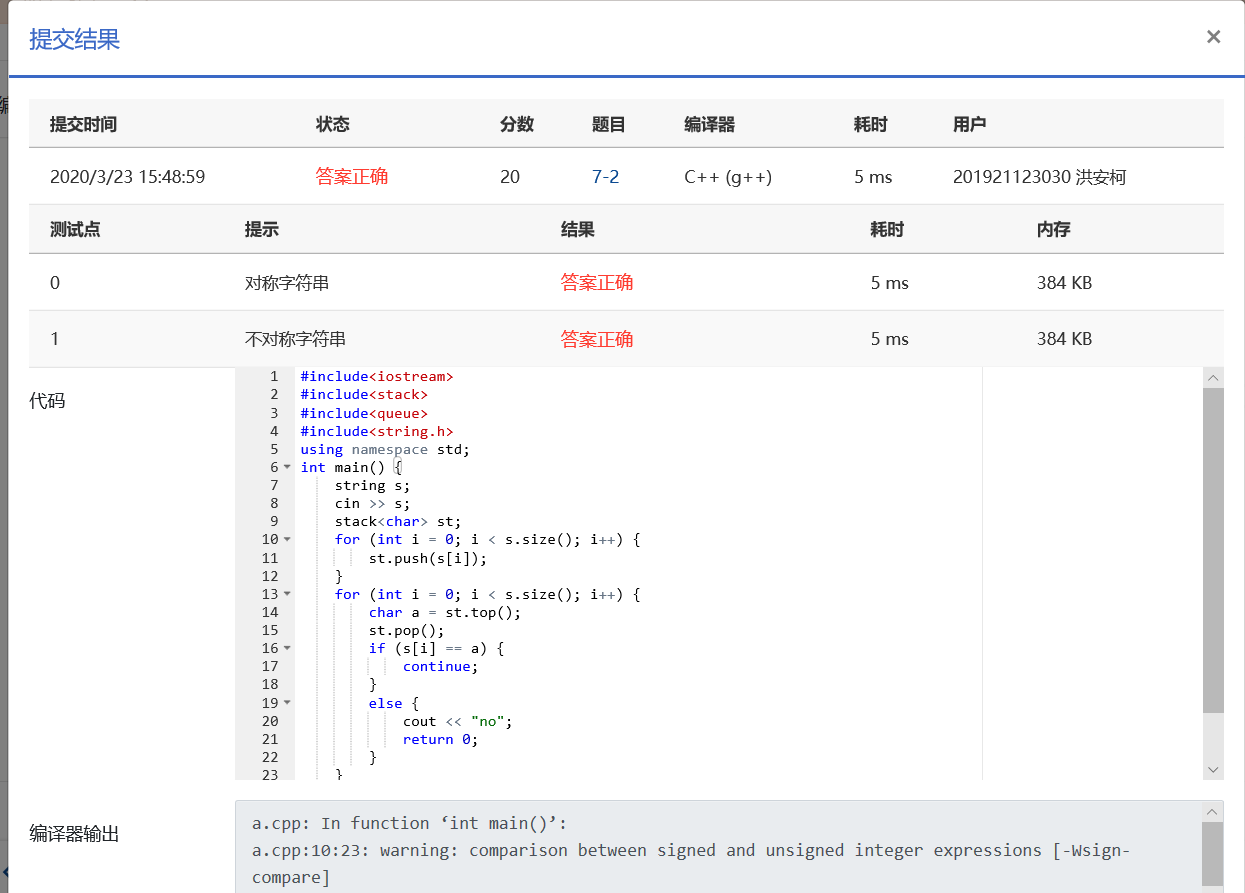
3.阅读代码
3.1 题目及解题代码


3.1.1 该题的设计思路
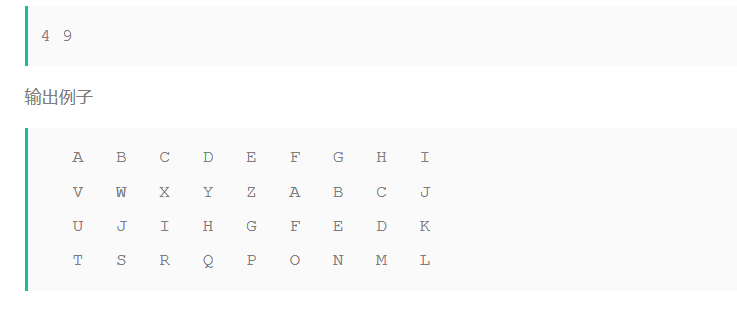
3.1.2 该题的伪代码
//我的思路是: 想象一个人在二维格子上走,边走边撒字母A-B-C...Z-A ,
//所以只需控制他走的方向 而且 并不难控制,因为他的方向总是右-下-左-上循环
#define M 10
#define N 20
int main(int argc, const char * argv[]) {
char MAP[M][N] = {0};
int r = 0,/*行*/ c = -1,/*列*/ p = 0,/*步数*/ dir = 1/*方向 1 右 2下 3左 4上*/;
//初始面向右边,身处第0行第-1列(没开始走进格子)
//开始走
for (; p < M * N; ) {
if (dir == 1) {
if (c + 1 <= N - 1 && MAP[r][c + 1] == 0)
{
//可以继续向右
c++;
MAP[r][c] = (p++) % 26 + 'A';
}
else {
//不能再向右,转到下一个方向
dir++;
}
}
if (dir == 2)
{
if (r + 1 <= M - 1 && MAP[r + 1][c] == 0)
{
r++;
MAP[r][c] = (p++) % 26 + 'A';
}
else
{
dir++;
}
}
if (dir == 3)
{
if (c - 1 >= 0 && MAP[r][c - 1] == 0)
{
c--;
MAP[r][c] = (p++) % 26 + 'A';
}
else
{
dir++;
}
}
if (dir == 4)
{
if (r - 1 >= 0 && MAP[r - 1][c] == 0)
{
r--;
MAP[r][c] = (p++) % 26 + 'A';
}
else
{
dir=1;
}
}
}
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{ printf("%c ", MAP[i][j]); }
printf("
");
}
return 0;
}