题目描述
学校联欢晚会的时候,为了使每一个同学都能参与进来,主持人常常会带着同学们玩击鼓传花的游戏。游戏规则是这样的:n个同学坐着围成一个圆圈,指定一个同学手里拿着一束花,主持人在旁边背对着大家开始击鼓,鼓声开始之后拿着花的同学开始传花,每个同学都可以把花传给自己左右的两个同学中的一个(左右任意),当主持人停止击鼓时,传花停止,此时,正拿着花没传出去的那个同学就要给大家表演一个节目。
聪明的小赛提出一个有趣的问题:有多少种不同的方法可以使得从小赛手里开始传的花,传了m次以后,又回到小赛手里。对于传递的方法当且仅当这两种方法中,接到花的同学按接球顺序组成的序列是不同的,才视作两种传花的方法不同。比如有3个同学1号、2号、3号,并假设小赛为1号,花传了3次回到小赛手里的方式有1->2->3->1和1->3->2->1,共2种。
输入
输入共一行,有两个用空格隔开的整数n,m(3<=n<=30,1<=m<=30)
样例输入
3 3
输出
输出共一行,有一个整数,表示符合题意的方法数
样例输出
2
思路1:动态规划
每个同学都可以把花传给自己左右的两个同学中的一个(左右任意);
假设同学编号为 1,2,3,4,5…i…n
正向思考:
-
- 第0次,1同学持有花,准备开始抛花。
- 第1次,同学2接到花 OR 同学n接到花。
反向思考:
-
- 第1个同学,可以收到第2个同学或者第n个同学的花。
- 第 i 个同学,可以收到第(i-1)个同学或者第(i+1)个同学的花。
- 第n个同学,可以收到第1个同学或者第(n-1)个同学的花。
总结:
-
- 第 i 次 j 接到花 = 第 i-1 次( j-1)接到花 + 第 i-1 次( j+1)接到花
- d[i][j] = d[(i-1)][(j-1)%n]+d[(i-1)][(j+1)%n] (为了很好的处理首尾两个元素使得环成立,这个公式得根据具体设置的数组进行调整)
- dp[i][j] 表示从初始节点走 i 步到达节点 j 所有的方法数
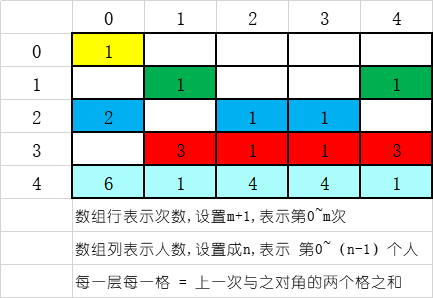
代码
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc=new Scanner(System.in); int n=sc.nextInt();//表示人数 int m=sc.nextInt();//表示经过的步数 int [][] dp=new int[m+1][n];//dp[i][j] 表示从初始节点0走i步到达节点j所有的方法数 dp[0][0]=1; for(int i=1;i<=m;i++){ for(int j=0;j<n;j++){ dp[i][j]=dp[(i-1)][(j-1+n)%n]+dp[(i-1)][(j+1+n)%n]; } } System.out.println(dp[m][0]); } }