1. 工作原理(定义)
选择排序(Selection sort)是一种简单直观的排序算法。它在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
2. 算法步骤
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
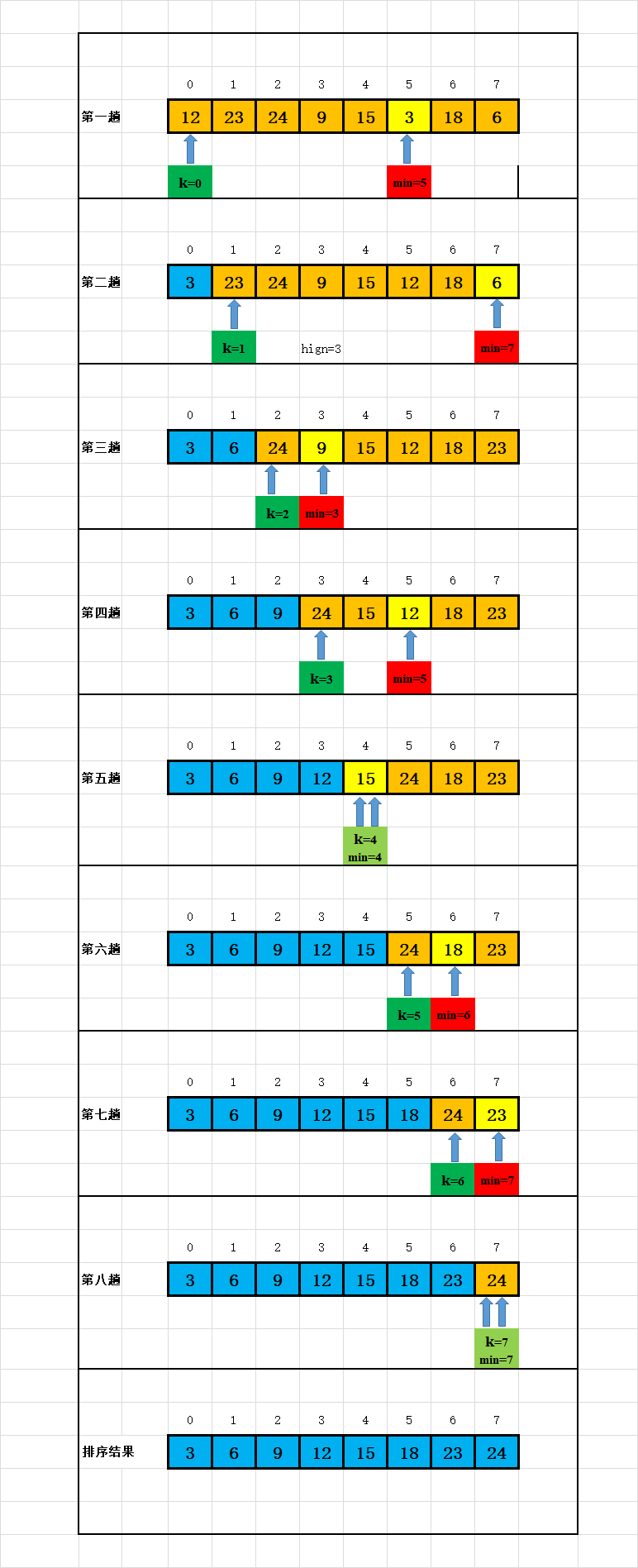
3. 动画演示
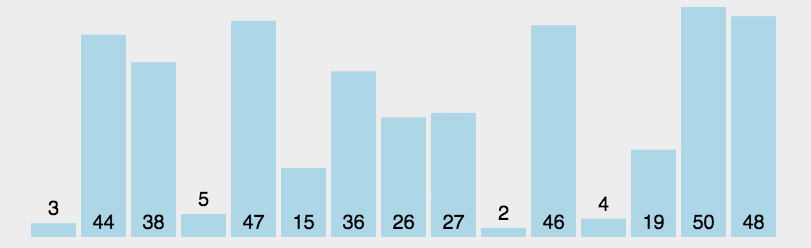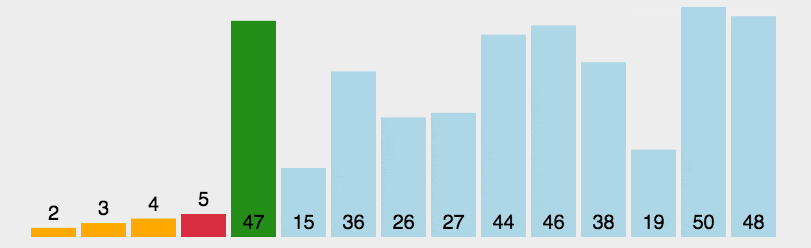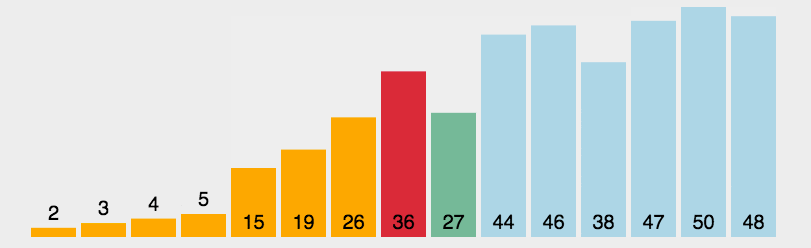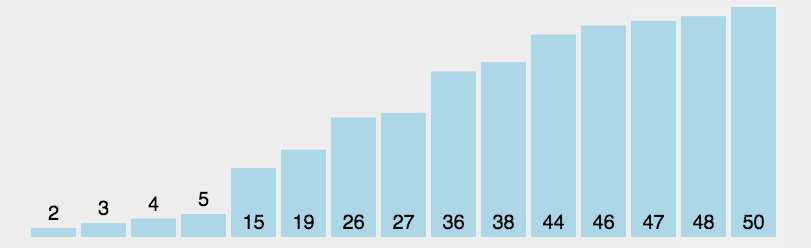
4. 性能分析
1. 时间复杂度
选择排序的比较次数为 n(n-1)/2,比较次数O(n^2),比较次数与关键字的初始状态无关,总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。
交换次数介于0和(n-1)次之间,交换次数O(n)。最好情况是,已经有序,交换0次;最坏情况交换n-1次,逆序交换n/2次。
赋值操作介于 0 和 3 (n - 1) 次之间。
故而在最优、最坏和平均情况下,其时间复杂度为 O(n^2)。
2. 空间复杂度
选择排序过程中,需要临时变量存储待排序元素,因此空间复杂度为O(1)。
3. 算法稳定性
选择排序是不稳定的算法,在选择数值和交换过程中它们的顺序可能会发生变化。
4. 初始顺序状态
- 比较次数:
- 移动次数:
- 复杂度:
- 排序趟数:无关
5. 归位
能归位,每一趟排序有一个元素归位。
6. 优点
- 相对于冒泡排序更快。
- 交换次数比冒泡排序少多了,由于交换所需CPU时间比比较所需的CPU时间多,n值较小时,选择排序比冒泡排序快。
- 数据规模越小越好。
6. 具体代码
public int[] selectionSort(int[] sourceArray){
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
// 每轮需要比较的次数 N-i
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 记录目前能找到的最小值元素的下标
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
/* 另一种交换方法
arr[min] = arr[min]^arr[i];
arr[i] = arr[min]^arr[i];
arr[min] = arr[min]^arr[i];
*/
}
}
return arr;
}