1. 题目
转自:原文
所谓回文数就是一个数字,从左边读和从右边读的结果都是一样的,例如12321。
现在有一个只包含1,2,3的数字,你可以通过在任意位置增加一位数字或者删除一位数字来将其变成一个回文数。但是增加或删除不同数字所需要的代价是不一样的。
已知增加和删除每个数字的代价如下:
* 增加一个 1,代价:100;删除一个 1,代价:120。
* 增加一个 2,代价:200;删除一个 2,代价:350。
* 增加一个 3,代价:360;删除一个 3,代价:200。
* 增加一个 4,代价:220;删除一个 4,代价:320。
请问如何通过最少的代价将一个数字变换为一个回文数。当然,如果一个数字本身已经是一个回文数(包括一位数,例如:2),那么变换的代价为 0。
输入描述:
单组输入。输入一个由1、2、3、4组成的正整数,正整数位数<=100位。【提示:采用字符串输入】
输出描述:
输出一个整数,表示将输入数字变换为一个回文数所需的最少代价。
2. 样例
输入:12322
输出:300
提示:
增加一个 1 并增加一个 2,将输入正整数变为 1223221 或者 2123212,所需代价最小,为:100+200=300。
3. 题解
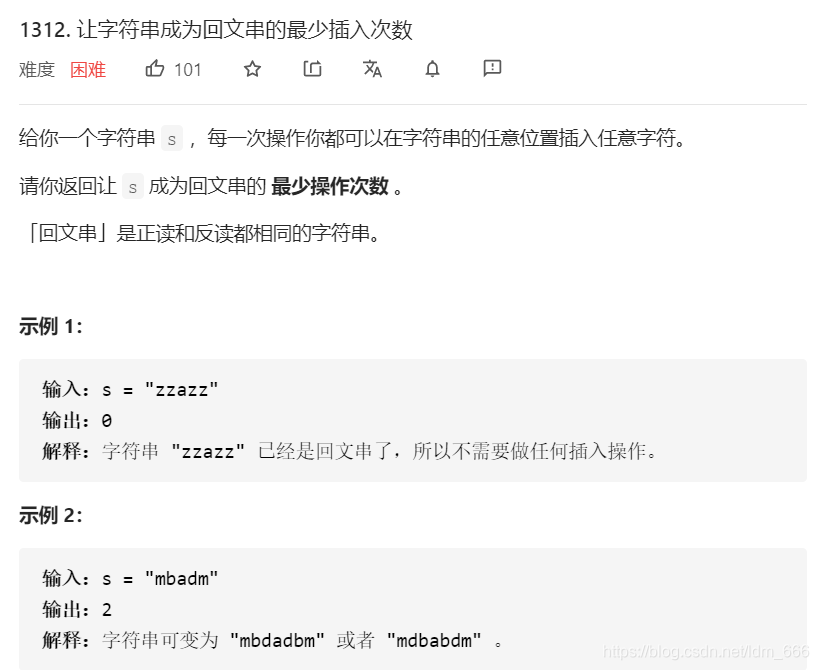
解答这道题后,原来的题目就很好解决了,首先回文串就是从左到右和从右到左遍历是完全一样的结果,这道题有两个思路,都是动态规划,找到状态转移方程求解,第一个是直接对原字符串分析,另一个是将字符串进行反转,求两个串的最长子序列的长度,然后总长度减去最长子序列的长度就是最少操作次数,有兴趣可以试一下这个思路。本文主要是说第一种方法,直接分析原字符串,找出状态转移方程,
首先,dp[i][j]表示字符串位置 i 到 j 为回文串的最少操作次数
当s[i]==s[j]时,dp[i][j]=dp[i+1][j-1] ,因为i位置和j位置上的字符相同,所以位置i到j的字符串变换操作次数取决于i到j中间的字符串变换为回文串的最少操作次数。
否则,说明i位置j位置上的字符不相同,那么i到j位置的字符串变换成回文串的操作次数取决去从i到j-1位置的操作次数和从i+1到j位置的操作次数,哪个小选择变换哪个。SO:
dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1;分析到此结束,看代码:(注意两层循环的设定,循环设置方式不唯一)
class Solution {
public:
int minInsertions(string s) {
int n = s.size();
vector<vector<int>>dp(n, vector<int>(n, 0));
for (int i = n - 2; i >= 0; i--)
{
for (int j = i + 1; j < n; j++)
{
if (s[i] == s[j])
dp[i][j] = dp[i + 1][j - 1];
else
{
dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1;
}
}
}
return dp[0][n-1];
}
};经过上面对于字符串变换的最小操作次数了解后,再回看这道变换为回文数的最小代价题。
首先根据题意,增加和删除的操作代价不相同,因为我们可以自己初始化一个最小代价数组,对于同一个数字,增加和删除的代价我们选择较小的那个。
所以可以定义一个数组arr[5]={0,100,200,200,220},数组的下标代表操作的数字,对应的值就代表操作该数字的代价,比如下标arr[1]=100表示对原串增加一个数字1,代价为100。(因为如果需要操作数字1,增加或删除肯定是选择代价更小的进行)
基于之前的分析,状态转移方程是一个道理,当s[i]==s[j]时,dp[i][j]=dp[i+1][j-1]
否则,我们不再是直接计算 dp[i][j]=min(dp[i+1][j],dp[i][j-1])+1;
因为上述不关心你操作的数据是多少,获得min(dp[i+1][j],dp[i][j-1])后需要操作字符s[i]还是s[j]不关心,因为不管操作哪一个都只是一次操作,但是本题需要比较不同的选择付出的代价。
我们有两个选择。选择操作s[i],dp[i][j]=arr[s[i]-'0']+dp[i+1][j] 即操作s[i]的代价加上i+1到j区间的字符串的代价;选择操作s[j],dp[i][j]=arr[s[j]-'0']+dp[i][j-1] 即操作s[j]的代价加上i到区间j+1的字符串的代价;我们选取两个选择中代价更小的一个作为dp[i][j]的值。 结合代码,如下:
1 public class n3 {
2 private static int[] add = {0, 100, 200, 360,220};
3 private static int[] dec = {0, 120, 350, 200, 320};
4 public static void main(String[] args) {
5 Scanner scanner = new Scanner(System.in);
6 String s = scanner.nextLine();
7 int n = s.length();
8 int[][] dp = new int[n][n];
9 for(int i = n - 1; i >=0; i--) {
10 for(int j = i + 1; j < n; j++) {
11 // 相等,只需要比较之间的数值
12 if(s.charAt(i) == s.charAt(j)) {
13 dp[i][j] = dp[i + 1][j - 1];
14 } else {
15 // 操作i
16 int dp1 = dp[i + 1][j] + Math.min(add[s.charAt(i) - '0'], dec[s.charAt(i) - '0']);
17 int dp2 = dp[i][j - 1] + Math.min(add[s.charAt(j) - '0'], dec[s.charAt(j) - '0']);
18 dp[i][j] = Math.min(dp1, dp2);
19 }
20 }
21 }
22 System.out.println(dp[0][n - 1]);
23 }
24 }4. 结语
努力去爱周围的每一个人,付出,不一定有收获,但是不付出就一定没有收获! 给街头卖艺的人零钱,不和深夜还在摆摊的小贩讨价还价。愿我的博客对你有所帮助(*^▽^*)(*^▽^*)!
如果客官喜欢小生的园子,记得关注小生哟,小生会持续更新(#^.^#)(#^.^#)。