Pytorch 四种边界填充方式(Padding)

1. 选用卷积之前填充（强烈建议）

　　 小生非常推荐大家不再使用卷积所带的填充方式，虽然那种方式简单，但缺陷太多。① 不能根据自己的需要来决定上与下填充不等的边界，左右填充不等的边界；② 边界填充零容易出现伪影的情况，对实验效果影响比较大。将卷积中的Padding方式换为卷积前Padding效果会更佳，以下列了四种填充方式（零填充，常数填充，镜像填充，复制填充）。

　　小生就不赘言了，客官请下观~~

2. 边界填充之零填充

　　零填充是常数填充的特例，这种填充方式和卷积中的填充的类似，都是填充零元素，不过这个比卷积填充更灵活，我们可以根据自己的需要再上下左右分别填充相应的0元素。

2.1 Code

import torch
import torch.nn as nn


# ==================  零填充  ==================
def conv_ZeroPad2d():
    # 定义一个四维数据：(batchSize, channel, height, width)
    data = torch.tensor([[[[1, 2, 3],
                           [4, 5, 6],
                           [7, 8, 9]]]]).float()
    print("data_shape: ", data.shape)
    print("data: ", data)
    # 零填充，在边界填充n个0,分别为：左、右、上、下
    ZeroPad = nn.ZeroPad2d(padding=(1, 2, 1, 2))
    data1 = ZeroPad(data)
    print("data1_shape: ", data1.shape)
    print("data1: ", data1)


if __name__ == '__main__':
    conv_ZeroPad2d()

2.2 结果显示

　　  可以看到，分别在左边填充1列0元素，右边填充2列0元素，上边填充1列0元素，下边填充2列0元素。

          

 3. 边界填充之常数填充

　　常数填充方式， 可以根据自己的需要在上下左右分别填充指定的元素。

3.1 Code

import torch


# ================== 常量填充 ==================
def conv_ConstantPad2d():
    # 定义一个四维数据：(batchSize, channel, height, width)
    data = torch.tensor([[[[1, 2, 3],
                           [4, 5, 6],
                           [7, 8, 9]]]]).float()
    print("data_shape: ", data.shape)
    print("data: ", data)
    # 用给定的纸填充，0填充是常亮填充的特列，分别为：左、右、上、下
    ConstantPad = nn.ConstantPad2d(padding=(1, 2, 1, 2), value=10)
    data1 = ConstantPad(data)
    print("data1_shape: ", data1.shape)
    print("data1: ", data1)


if __name__ == '__main__':
    conv_ConstantPad2d()

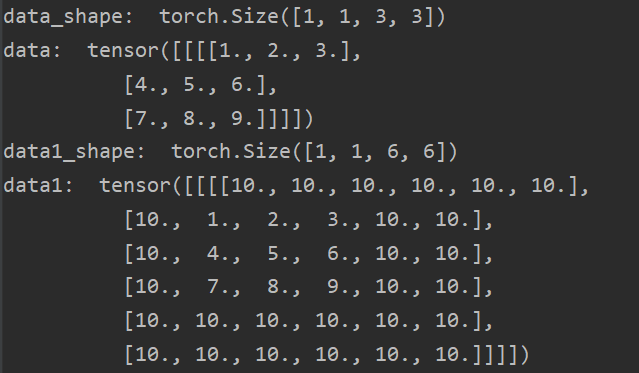
3.2 结果显示

　　可以看到，分别在左边填充1列10元素，右边填充2列10元素，上边填充1列10元素，下边填充2列10元素。

       

4. 边界填充之镜像填充

   镜像填充方式是根据对称性来填充的。

4.1 Code

import torch 


# ================== 镜像填充 ==================
def conv_ReflectionPad2d():
    # 定义一个四维数据：(batchSize, channel, height, width)
    data = torch.tensor([[[[1, 2, 3],
                           [4, 5, 6],
                           [7, 8, 9]]]]).float()
    print("data_shape: ", data.shape)
    print("data: ", data)
    # 复制边界n次，分别为：左、右、上、下
    ReflectionPad = nn.ReflectionPad2d(padding=(1, 2, 1, 2))
    data1 = ReflectionPad(data)
    print("data1_shape: ", data1.shape)
    print("data1: ", data1)


if __name__ == '__main__':
    conv_ReflectionPad2d()

4.2 结果显示

 

5. 边界填充之复制填充

　　复制填充方式，小生非常推荐。复制填充是复制最外边界的元素来填充，这样填充的元素与边界元素相近，对实验结果的影响会降到最小。

5.1 Code

import torch


# ================== 重复填充 ==================
def conv_ReplicationPad2d():
    # 定义一个四维数据：(batchSize, channel, height, width)
    data = torch.tensor([[[[1, 2, 3],
                           [4, 5, 6],
                           [7, 8, 9]]]]).float()
    print("data_shape: ", data.shape)
    print("data: ", data)
    # 用对称位置的像素来填充,分别为：左、右、上、下
    ReplicationPad = nn.ReplicationPad2d(padding=(1, 2, 1, 2))
    data1 = ReplicationPad(data)
    print("data1_shape: ", data1.shape)
    print("data1: ", data1)


if __name__ == '__main__':
    conv_ReplicationPad2d()

5.2 结果显示

　　 可以看到，填充的元素与最外边界的元素相同。

  

 6. 总结

　　努力去爱周围的每一个人，付出，不一定有收获，但是不付出就一定没有收获！ 给街头卖艺的人零钱，不和深夜还在摆摊的小贩讨价还价。愿我的博客对你有所帮助(*^▽^*)(*^▽^*)！

　　如果客官喜欢小生的园子，记得关注小生哟，小生会持续更新(#^.^#)(#^.^#)！