多特征(Multiple features)
本节将两个特征(其中x0=1)延伸到多个特征(变量),“特征”看来就是自变量、影响因子,比如价格是因变量,房屋面积、房间数、层数、房龄等是自变量或影响因子。
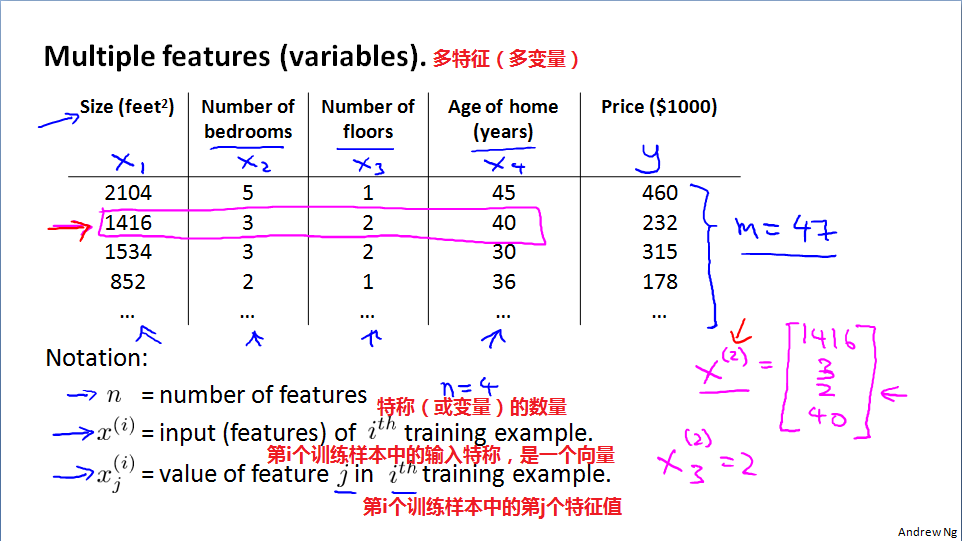
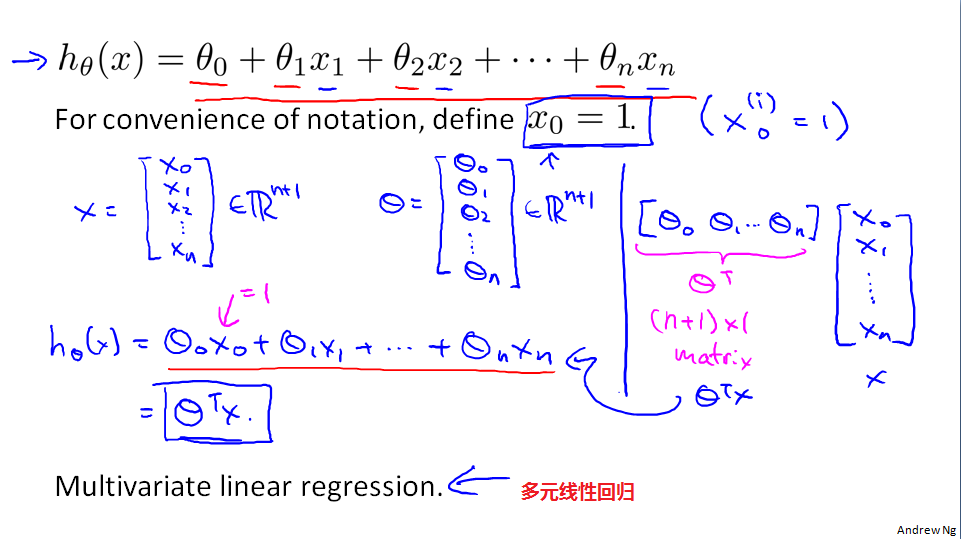
多元线性回归
多元梯度下降法(Gradient descent for Multiple variables)

多元线性回归的梯度下降的方法,分别对不同的参数进行偏导数。
梯度下降法:特征缩放(Featrue Scaling)
特征缩放:瘦长的椭圆,会导致趋向最值时梯度下降的震荡;所以需要缩放特征值,使得其取值范围相近。

、
缩放的特征值尽量在-1到1之间,当然,范围在-3到3之间,或者-1/3到1/3之间也是可以接受的。

均值归一化,(特征值-均值)/标准差,其中,标准差为最大值减去最小值。

梯度下降法:学习率(Learning Rate)
学习率选择时,学习率太小,收敛过慢;学习率太大,代价函数与步数之间的曲线可能不是下降,甚至无法收敛。
那么,如何选择学习率呢?一般按照3的倍数去取,如.......0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1..........

正规方程(Normal equation)
可以一步得到回归问题的最优解,不需要进行特征缩放,适用于特征量不是很大的时候,一般不适用特别复杂的函数。

正规方程的具体公式,
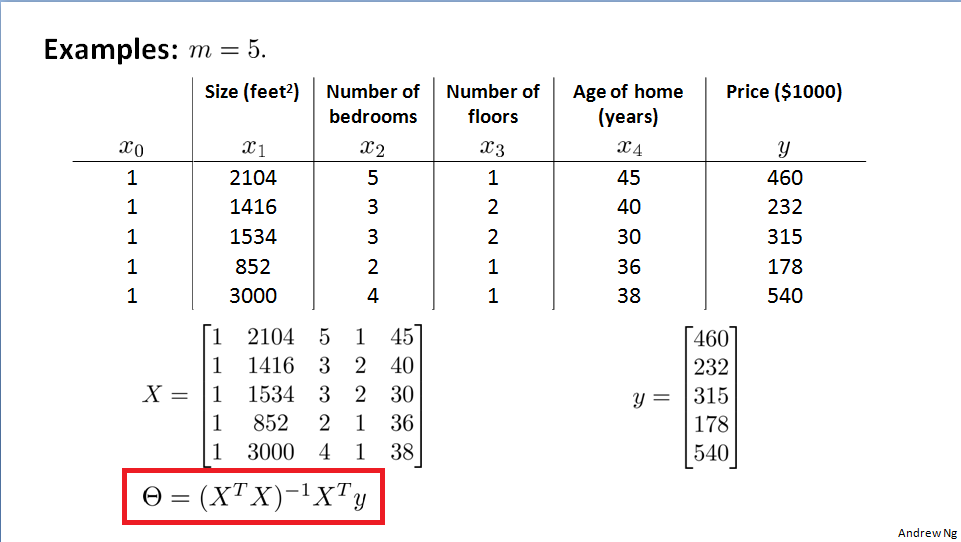
正规方程在Octave上的实现形式

那么,应该什么时候使用正规方程,什么时候使用梯度下降呢?

一般情况下,n<10000时,使用正规方程;当n>10000时,就需要考虑使用梯度下降法。