题目:http://www.rqnoj.cn/problem/123
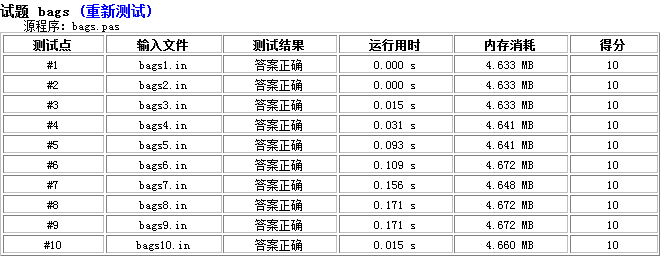
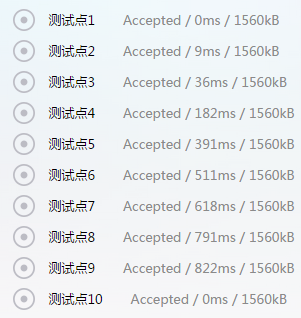
不得不说,RQNOJ 的机子跑得好慢呀,5*107 的数据范围本地跑 0.2s,服务器上愣是把我卡掉了,最后只好写了一份 Pascal 交上去
本地跑
OJ上跑
咳咳,言归正传
普通的背包是求出最优的那一钟方案,方程转移是 f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]),相当于把 2 个变量经比较后丢到 1 个变量里,也就是 k=1时的情况
而现在我们需要求最优的前 k 组方案,那么可以把数组再增加一维,变成把 2k 个变量经比较后丢进k个数里,也就是 2 个线性表丢进 1 个线性表里,由于线性表内数据是单调下降的,则可以按照归并排序的做法做
实现操作中还可以滚掉第一维,那么 j 就要递减枚举
以下是 C++ 的,但是会TLE
1 #include<algorithm> 2 #include<iostream> 3 #include<cstdlib> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 using namespace std; 8 9 const int V=5001,K=51,maxint=2147483647; 10 int f[V][K],g[K]; 11 int main() 12 { 13 int i,j,n,m,s,ans=0,q1,q2,k,w,v; 14 scanf("%d%d%d",&m,&s,&n); 15 for (i=0;i<=s;i++) 16 for (j=1;j<=m;j++) f[i][j]=-maxint; 17 f[0][1]=0; 18 for (i=1;i<=n;i++) 19 { 20 scanf("%d%d",&w,&v); 21 for (j=s;j>=w;j--) 22 { 23 if (f[j-w][1]<0) continue; 24 q1=q2=1; 25 for (k=1;k<=m;k++) 26 if (f[j-w][q1]+v>f[j][q2]) g[k]=f[j-w][q1++]+v; 27 else g[k]=f[j][q2++]; 28 for (k=1;k<=m;k++) f[j][k]=g[k]; 29 } 30 } 31 for (i=1;i<=m;i++) ans+=f[s][i]; 32 printf("%d ",ans); 33 return 0; 34 }
这个是 Pascal 的,可以AC
1 program xqz; 2 uses math; 3 const maxv=5000; maxk=51; 4 type arr=array[0..maxk] of longint; 5 var 6 c,w,i,j,m,n,k,mv,mk,l,r,b,p,e,s,t,v:longint; 7 yes:boolean; 8 f:array[0..maxv,0..maxk] of longint; 9 ans,now:int64; 10 procedure work(var a:arr; b,c:arr); 11 var l,r:longint; 12 begin 13 l:=1; r:=1; 14 while (l+r-2<mk)and ((b[l]<>-1)or(c[r]<>-1)) do 15 begin 16 while (b[l]<>-1)and((c[r]=-1)or(b[l]>=c[r]+w))and(l+r-2<mk) do 17 begin 18 a[l+r-1]:=b[l]; inc(l); 19 end; 20 while (c[r]<>-1)and((b[l]=-1)or(b[l]<=c[r]+w))and(l+r-2<mk) do 21 begin 22 a[l+r-1]:=c[r]+w; inc(r); 23 end; 24 end; 25 end; 26 27 begin 28 readln(mk,mv,n); fillchar(f,sizeof(f),$ff); 29 f[0,1]:=0; 30 for i:=1 to n do 31 begin 32 readln(c,w); now:=now+c; 33 for j:=min(now,mv) downto c do 34 work(f[j],f[j],f[j-c]) 35 end; 36 for k:=1 to mk do 37 inc(ans,f[mv,k]); 38 writeln(ans); 39 close(input); close(output); 40 end.
版权所有,转载请联系作者,违者必究
QQ:740929894