[ CodeVS冲杯之路 ] P1166

　　不充钱，你怎么AC？

　　题目：http://codevs.cn/problem/1166/

　　有许久没有刷题了，忙着过中秋去了嘿嘿

　　首先它的每一行是独立的，我们可以直接把它拆分成 n 互不相关的子问题做

　　那么就变成了区间 DP 问题，f[i][j] 表示在区间 [i,j] 内的最大分数，首先枚举区间长度 k，然后再枚举左端点 i

　　 　

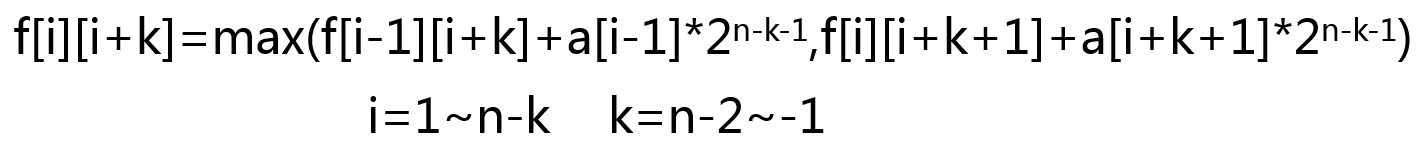
　　n 表示的是一行数的个数

　　注意 k 要到-1，是因为 f[i][i] 时还有一个 a[i] 没有取走，目标状态是 max ( f[i][i-1] ) ,（i=1~n）

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define N 90
using namespace std;

long long a[N],f[N][N],m,ans,t,n;
int main()
{
    long long i,k;
    cin>>t>>n;
    while (t>0)
    {
        t--;
        for (i=1;i<=n;i++) cin>>a[i];
        for (k=n-2;k>=-1;k--)
        {
            for (i=1;i<=n-k;i++)
            {
                f[i][i+k]=max(f[i-1][i+k]+a[i-1]*(1<<(n-k-1)),f[i][i+k+1]+a[i+k+1]*(1<<(n-k-1)));
            }
        }
        m=0;
        for (i=1;i<=n;i++) m=max(m,f[i][i-1]);
        ans+=m;
    }
    cout<<ans<<endl;
    return 0;
}

　　这段代码交上去只有60分，是为什么呢？

　　查了很久的问题，结果返回一看题目数据范围，要写高精度……当年应该觉得这道题太简单了，于是就放个高精度卡掉选手40分

　　那么就写一个高精度的加法和比较大小即可，直接贴别人的代码嘿嘿

#include<cstdio>
#include<cstring>
#include<iostream>
#define maxn 100
#define base 10000
using namespace std;

int n,m,cnt=1,lp[85],rp[85];
int map[85][85];
struct Bign
{
    int c[maxn],len;
    Bign ()
    {
        memset(c,0,sizeof(c)),len=1;
    }
    void Zero()
    {
        while(len>1&&c[len]==0)len--;
    }
    void Write(char *s)
    {
    int l=strlen(s);
    int k=1;
    for(int i=l-1;i>=0;i--)
    {
        c[len]+=k*(s[i]-'0');
        k*=10;
        if(k==base)
        {
            k=1;len++;
        }
    }
}
void Read()
{
    char s[maxn];
    scanf("%s",s);
    Write(s);
}
void Print()
{
    printf("%d",c[len]);
    for(int i=len-1;i>=1;i--) printf("%04d",c[i]);
    printf("
");
}
Bign operator = (const int &a)
{
    memset(c,0,sizeof(c));
    len=1;
    char s[maxn];
    sprintf(s,"%d",a);
    Write(s);
    Zero();
    return *this;
}
Bign operator +(const Bign &a)
{
    Bign r;
    r.len=max(len,a.len)+1;
    for(int i=1;i<=r.len;i++)
    {
        r.c[i]+=c[i]+a.c[i];
        r.c[i+1]+=r.c[i]/base;
        r.c[i]%=base;
    }
    r.Zero();
    return r;
}
Bign operator +(const int &a)
{
    Bign b;
    b=a;
    return *this+b;
}
Bign operator *(const Bign &a)
{
    Bign r;
    r.len=len+a.len+2;
    for(int i=1;i<=len;i++)
    {
        for(int j=1;j<=a.len;j++)
        {
            r.c[i+j-1]+=c[i]*a.c[j];
        }
    }
    for(int i=1;i<=r.len;i++)
    {
        r.c[i+1]+=r.c[i]/base;
        r.c[i]%=base;
    }
    r.Zero();
    return r;
}
Bign operator *(const int &a)
{
    Bign b;
    b=a;
    return *this*b;
}
bool operator < (const Bign &b)const
{
    if(len!=b.len) return len<b.len;
    else
    {
        for(int i=len;i>=1;i--)
        {
            if(c[i]!=b.c[i]) return c[i]<b.c[i];
        }
    }
    return 0;
}
bool operator >(const Bign &b)const
{
    return b<*this;
}
bool operator <=(const Bign &b)const
{
    return !(b>*this);
}
bool operator >=(const Bign &b)const
{
    return !(b<*this);
}
bool operator == (int a)
{
    return len==1 && c[len]==a;
}
};
Bign f[85][85];
Bign Max(Bign a,Bign b)
{
    if(a>=b) return a;
    if(a<b) return b;
}
int main()
{
    Bign ans;
    ans=0;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&map[i][j]);
        }
    }
    for (int i=1;i<=n;i++)
    {
           for(int u=1;u<=m;u++)
            for(int v=1;v<=m;v++) f[v][u]=0;
        for (int j=1;j<=m;j++)
        {
            f[j][j]=map[i][j]*2;
           }
        for(int len=1;len<=m-1;len++)
        {
            for(int l=1;l<=m&&l+len<=m;l++)
            {
                Bign k;
                k=max(f[l+1][l+len]+map[i][l],f[l][l+len-1]+map[i][l+len]);
                f[l][l+len]=k*2;
            }
        }
        ans=ans+f[1][m];
    }
    ans.Print() ;
    return 0 ;
}