图的算法-最短路径算法

转载：[图的最短路径算法]Dijkstra, Bellman-Ford, Floyd-Warshall

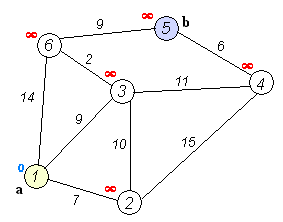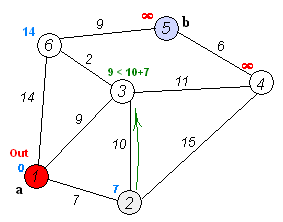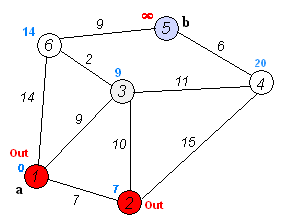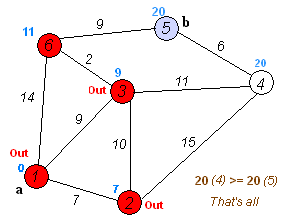
一. Dijkstra算法

⚠️ 注意：不能解决含有负权的图。

S[v]标记已访问（红色节点）：queue.pop后，再标记已访问。

priority_queue优先队列：优先处理最短节点。

dis[v]：节点v到其实节点Start的最短距离。

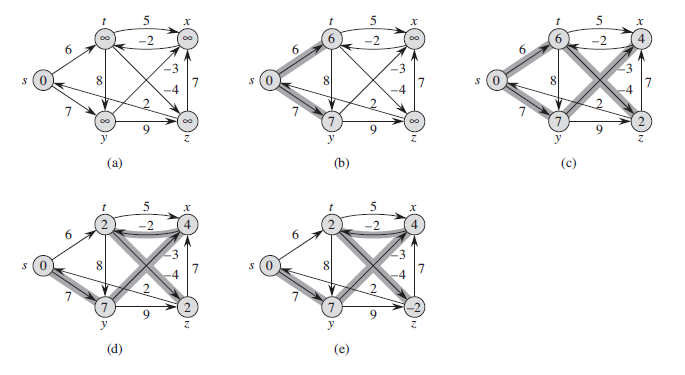
 二、Bellman-Ford算法

全图松弛操作：次数最多n次（节点个数）

dis[Start]=0，else: dis[v]=∞

每次全图松弛：只可能松弛到dis[cur]!=∞的邻接节点。

因为：要判断dis[cur]+w<dis[nextn]中，dis[cur]肯定!=∞

证明该图存在负环：n次以后，若还能继续松弛：dis[cur]+w<dis[nextn]。

三、Floyd-Warshall算法

⚠️ 注意：不能处理存在负权回路的图（但可处理含有负权边的图）

算法思想原理： 

     Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在） 

      从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。 

typedef struct
{
    char vertex[VertexNum];                                //顶点表
    int edges[VertexNum][VertexNum];                       //邻接矩阵,可看做边表
    int n,e;                                               //图中当前的顶点数和边数
}MGraph;

void Floyd(MGraph g)
{
 　　int A[MAXV][MAXV];
 　　int path[MAXV][MAXV];
 　　int i,j,k,n=g.n;
 　　for(i=0;i<n;i++)
    　　for(j=0;j<n;j++)
    　　{
             A[i][j]=g.edges[i][j];
         　　 path[i][j]=-1;
     　 }
 　　for(k=0;k<n;k++)
 　　{
      　　for(i=0;i<n;i++)
         　　for(j=0;j<n;j++)
             　　if(A[i][j]>(A[i][k]+A[k][j]))
             　　{
                   　　A[i][j]=A[i][k]+A[k][j];
                   　　path[i][j]=k;
              　 }
    　}
}