问题:
求给定无向图(树),从那个顶点作为root,得到最矮树。
Example 1: Input: n = 4, edges = [[1,0],[1,2],[1,3]] Output: [1] Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT. Example 2: Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]] Output: [3,4] Example 3: Input: n = 1, edges = [] Output: [0] Example 4: Input: n = 2, edges = [[0,1]] Output: [0,1] Constraints: 1 <= n <= 2 * 104 edges.length == n - 1 0 <= ai, bi < n ai != bi All the pairs (ai, bi) are distinct. The given input is guaranteed to be a tree and there will be no repeated edges.
解法:BFS
该问题,看作无向图的遍历,
从图中哪个节点开始遍历,使得到leaf节点的距离最短。
首先根据邻边关系,构建图:
- nodemp[i]={a,b,c...}
- 代表:i-a, i-b, i-c...
我们可有以下思路:
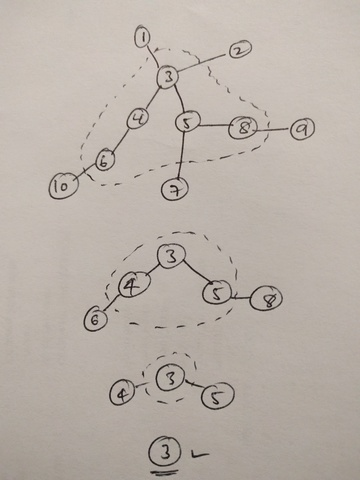
- 要找到离四周leaf节点都很近的中间节点,
- 那就从四周leaf节点同时向内,蚕食。
- 最后剩下的节点,即为到四周步数一样的解。
具体逻辑:
- queue中首先保存所有nodemp[i].size==1的节点。(即:leaf节点)
- ⚠️ 注意:由于最后要求的是最后一次(下一次queue为空)剩下queue里的这一层节点。
- 因此使用tmpq,来保存处理该层queue之前queue的状态。
- 开始遍历:
- LOOP:
- 处理最外层叶子节点:对于每个节点cur:
- 删除该节点+该节点与相邻节点的连线:
- nodemp[cur](删除,可不做,因为cur已被pop,就不再会加入queue中处理了)
- for every nextn : nodemp[cur]
- nodemp[nextn].erase(cur).
- 判断是否加入queue:该邻接节点nextn也成为了叶子节点:nodemp[nextn].size==1
- 处理最外层叶子节点:对于每个节点cur:
- 最终返回最后一次queue的状态:tmpq->res
代码参考:
1 class Solution { 2 public: 3 vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) { 4 vector<int> res; 5 vector<unordered_set<int>> nodemp(n, unordered_set<int>()); 6 //vector<pair<vector<int>,unordered_set<int>>> proc(n); 7 queue<int> q; 8 if(n==1) return {0}; 9 for(auto ed:edges) { 10 nodemp[ed[0]].insert(ed[1]); 11 nodemp[ed[1]].insert(ed[0]); 12 } 13 for(int i=0; i<n; i++) { 14 //add all leaf node to queue 15 if(nodemp[i].size()==1) q.push(i); 16 } 17 queue<int> tmpq; 18 while(!q.empty()) { 19 int sz = q.size(); 20 tmpq = q; 21 for(int i=0; i<sz; i++) { 22 int cur = q.front(); 23 q.pop(); 24 for(int nextn:nodemp[cur]) { 25 //delete the leaf node(cur) with the line connected its nextn. 26 nodemp[nextn].erase(cur); 27 //nodemp[cur].erase(nextn); 28 if(nodemp[nextn].size()==1) q.push(nextn); 29 } 30 } 31 } 32 while(!tmpq.empty()) { 33 res.push_back(tmpq.front()); 34 tmpq.pop(); 35 } 36 return res; 37 } 38 };