( ext{Solution:})
简单个鬼 sto zzq
化式子:
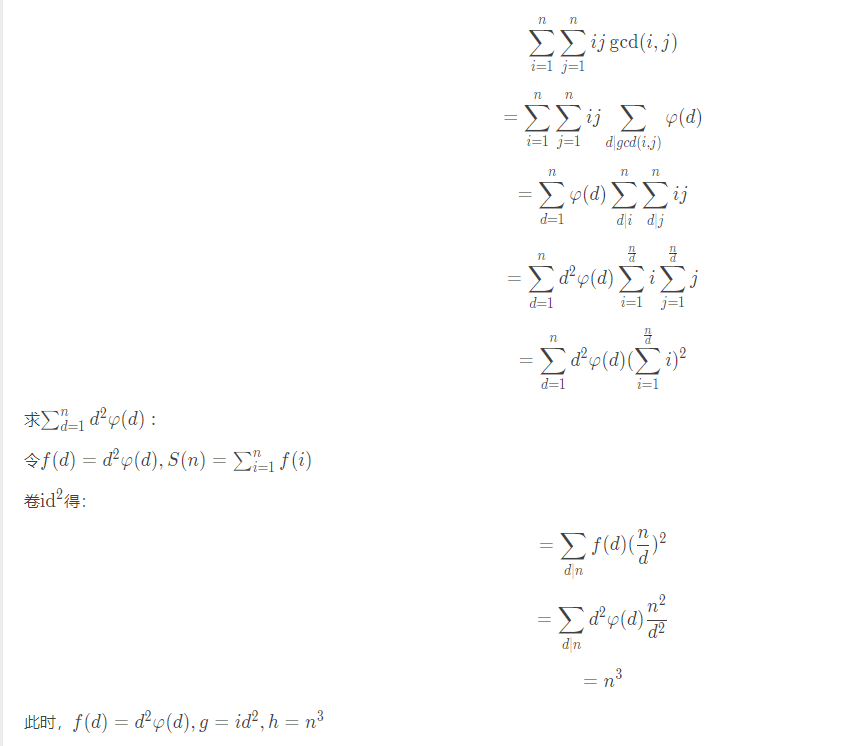
杜教筛求解即可。
这题卡常……笔者菜鸡卡不过去,加了火车头。
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define int long long
int p,n,inv2,inv6;
inline int add(int x,int y){return (x%p+y%p)%p;}
inline int mul(int x,int y){return 1ll*((x%p)*(y%p))%p;}
const int MAXN=5e7;
int pii[MAXN+10],pr[MAXN+10],cnt,N;
bitset<MAXN+10>vis;
void predo(){
pii[1]=1;
for(int i=2;i<=N;++i){
if(!vis[i])pr[++cnt]=i,pii[i]=i-1;
for(int j=1;j<=cnt&&i*pr[j]<=N;++j){
vis[i*pr[j]]=1;
if(i%pr[j]==0){
pii[i*pr[j]]=mul(pii[i],pr[j]);
break;
}
pii[i*pr[j]]=mul(pii[i],pr[j]-1);
}
}
for(int i=2;i<=N;++i)pii[i]=mul(pii[i],mul(i,i)),pii[i]=add(pii[i],pii[i-1]);
}
inline int qpow(int a,int b){
int res=1;
while(b){
if(b&1)res=mul(res,a);
a=mul(a,a);b>>=1;
}
return res;
}
inline int s3(ll x){x%=p;return mul(mul(x,mul(x+1,inv2)),mul(x,mul(x+1,inv2)));}
inline int s2(ll x){x%=p;return mul(inv6,mul(x,mul(x+1,x+x+1)));}
map<int,int>mp;
int getp(ll n){
if(n<=N)return pii[n];
if(mp.count(n))return mp[n];
ll res=s3(n);
for(ll l=2,r;l<=n;l=r+1){
r=n/(n/l);
(res-=mul((s2(r)-s2(l-1)+p)%p,getp(n/l)%p))%=p;
}
res+=p;res%=p;
return mp[n]=res;
}
int solve(ll n){
int res=0;
for(ll l=1,r;l<=n;l=r+1){
r=(n/(n/l));
res=add(res,mul((getp(r)-getp(l-1)+p)%p,s3(n/l)));
}
return res;
}
signed main(){
scanf("%d%lld",&p,&n);
N=pow(n,0.66666666);N+=N;predo();
inv2=qpow(2,p-2);inv6=qpow(6,p-2);
printf("%d
",solve(n));
return 0;
}
各位大佬有更好的卡常方法欢迎来指教。