You are given a map in form of a two-dimensional integer grid where 1 represents land and 0 represents water.
Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn't have "lakes" (water inside that isn't connected to the water around the island). One cell is a square with side length 1. The grid is rectangular, width and height don't exceed 100. Determine the perimeter of the island.
Example:
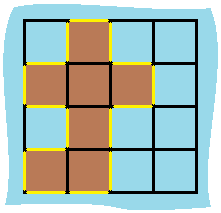
Input: [[0,1,0,0], [1,1,1,0], [0,1,0,0], [1,1,0,0]] Output: 16 Explanation: The perimeter is the 16 yellow stripes in the image below:
Approach #1: C++.
class Solution {
public:
int islandPerimeter(vector<vector<int>>& grid) {
int row = grid.size();
int col = grid[0].size();
int res = 0;
for (int i = 0; i < row; ++i) {
for (int j = 0; j < col; ++j) {
if (grid[i][j] == 1) {
res += check(grid, i, j);
}
}
}
return res;
}
private:
int check(vector<vector<int>> grid, int i, int j) {
int num = 0;
if (i == 0 || grid[i-1][j] == 0) num++;
if (i == grid.size() - 1 || grid[i+1][j] == 0) num++;
if (j == 0 || grid[i][j-1] == 0) num++;
if (j == grid[0].size() - 1 || grid[i][j+1] == 0) num++;
return num;
}
};
Approach #2: Java.
class Solution {
public int islandPerimeter(int[][] grid) {
int islands = 0, neighbours = 0;
for (int i = 0; i < grid.length; ++i) {
for (int j = 0; j < grid[0].length; ++j) {
if (grid[i][j] == 1) {
islands++;
if (i < grid.length - 1 && grid[i+1][j] == 1) neighbours++;
if (j < grid[0].length - 1 && grid[i][j+1] == 1) neighbours++;
}
}
}
return islands * 4 - neighbours * 2;
}
}
Approach #3: Python.
class Solution(object):
def islandPerimeter(self, grid):
h = len(grid)
w = len(grid[0])
extended_grid = [[0]*(w+2)] + [[0] + row + [0] for row in grid] + [[0]*(w+2)]
perimeter = 0
for i in range(h+1):
for j in range(w+1):
if extended_grid[i][j] != extended_grid[i][j+1]:
perimeter += 1
if extended_grid[i][j] != extended_grid[i+1][j]:
perimeter += 1
return perimeter
| Time Submitted | Status | Runtime | Language |
|---|---|---|---|
| a few seconds ago | Accepted | 188 ms | python |
| 9 hours ago | Accepted | 65 ms | java |
| 10 hours ago | Accepted | 656 ms | cpp |
In the approach 2, we know that the number of peimeter equal to the grids' edge substract the neigbours grids' edge which at it's down or right direction.