Weekly Contest 113

949. Largest Time for Given Digits (string::compare)

Given an array of 4 digits, return the largest 24 hour time that can be made.

The smallest 24 hour time is 00:00, and the largest is 23:59.  Starting from 00:00, a time is larger if more time has elapsed since midnight.

Return the answer as a string of length 5.  If no valid time can be made, return an empty string.

Example 1:

Input: [1,2,3,4]
Output: "23:41"

Example 2:

Input: [5,5,5,5]
Output: ""

Note:

1. A.length == 4
2. 0 <= A[i] <= 9

class Solution {
public:
    string largestTimeFromDigits(vector<int>& A) {
        check(A[0], A[1], A[2], A[3]);
        check(A[0], A[2], A[1], A[3]);
        check(A[0], A[3], A[1], A[2]);
        check(A[1], A[2], A[0], A[3]);
        check(A[1], A[3], A[0], A[2]);
        check(A[2], A[3], A[0], A[1]);
        return ans;
    }
    
    void check(int h1, int h2, int m1, int m2) {
        string hour = best(h1, h2, 24);
        string minute = best(m1, m2, 60);
        if (hour == "" || minute == "") return ;
        
        string cand = hour + ":" + minute;
        if (ans.compare(cand) < 0) ans = cand;
    }
    
    string best(int d1, int d2, int limit) {
        int ans = max(d1*10 + d2 < limit ? d1*10 + d2 : -1,
                      d2*10 + d1 < limit ? d2*10 + d1 : -1);
        string res = "";
        if (ans < 0) return res;
        else {
            if (ans < 10) {
                res += "0";
                res += to_string(ans);
            } else {
                res += to_string(ans);
            }
        }
        return res;
    }
    
private:
    string ans = "";
    
};

In this problem, we can use difference functions to solve the sub questions, At the first time I try to use if statement to solve difference case, finally, I failed. It's too complicate to deal with all cases.

And In C we can use strcmp to compare two string (char* str[]), but in C++ we have to use string::compare. if str1.compare(str2) < 0, it represent str1 isn't match with str2, and lower in the compare string.

 951. Flip Equivalent Binary Trees

For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.

A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.

Write a function that determines whether two binary trees are flip equivalent.  The trees are given by root nodes root1 and root2.

Example 1:

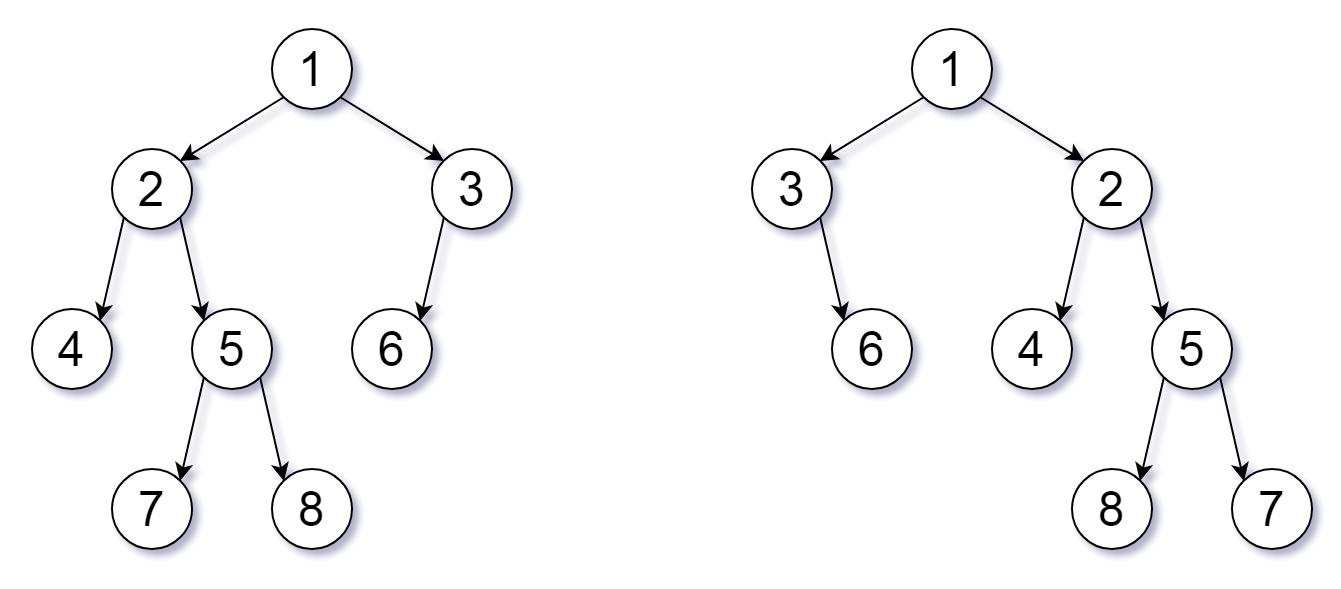
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.

Note:

1. Each tree will have at most 100 nodes.
2. Each value in each tree will be a unique integer in the range [0, 99].

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool flipEquiv(TreeNode* root1, TreeNode* root2) {
        if (root1 == root2)
            return true;
        if (root1 == nullptr || root2 == nullptr || root1->val != root2->val)
            return false;
        return (flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right) ||
                flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left));
    }
};

950. Reveal Cards In Increasing Order

In a deck of cards, every card has a unique integer.  You can order the deck in any order you want.

Initially, all the cards start face down (unrevealed) in one deck.

Now, you do the following steps repeatedly, until all cards are revealed:

1. Take the top card of the deck, reveal it, and take it out of the deck.
2. If there are still cards in the deck, put the next top card of the deck at the bottom of the deck.
3. If there are still unrevealed cards, go back to step 1.  Otherwise, stop.

Return an ordering of the deck that would reveal the cards in increasing order.

The first entry in the answer is considered to be the top of the deck.

Example 1:

Input: [17,13,11,2,3,5,7]
Output: [2,13,3,11,5,17,7]
Explanation: 
We get the deck in the order [17,13,11,2,3,5,7] (this order doesn't matter), and reorder it.
After reordering, the deck starts as [2,13,3,11,5,17,7], where 2 is the top of the deck.
We reveal 2, and move 13 to the bottom.  The deck is now [3,11,5,17,7,13].
We reveal 3, and move 11 to the bottom.  The deck is now [5,17,7,13,11].
We reveal 5, and move 17 to the bottom.  The deck is now [7,13,11,17].
We reveal 7, and move 13 to the bottom.  The deck is now [11,17,13].
We reveal 11, and move 17 to the bottom.  The deck is now [13,17].
We reveal 13, and move 17 to the bottom.  The deck is now [17].
We reveal 17.
Since all the cards revealed are in increasing order, the answer is correct.

Note:

1. 1 <= A.length <= 1000
2. 1 <= A[i] <= 10^6
3. A[i] != A[j] for all i != j

 

class Solution {
public:
    vector<int> deckRevealedIncreasing(vector<int>& deck) {
        int N = deck.size();
        queue<int> q;
        for (int i = 0; i < N; ++i) {
            q.push(i);
        }
        vector<int> ans(N);
        sort(deck.begin(), deck.end());
        for (int card : deck) {
            ans[q.front()] = card;
            if (!q.empty()) {
                q.pop();
                q.push(q.front());
                q.pop();
            }
        }
        return ans;
    }
};

　　

It's very clever to use a queue to simulation the process.

952. Largest Component Size by Common Factor

Given a non-empty array of unique positive integers A, consider the following graph:

• There are A.length nodes, labelled A[0] to A[A.length - 1];
• There is an edge between A[i] and A[j] if and only if A[i] and A[j] share a common factor greater than 1.

Return the size of the largest connected component in the graph.

Example 1:

Input: [4,6,15,35]
Output: 4

Example 2:

Input: [20,50,9,63]
Output: 2

Example 3:

Input: [2,3,6,7,4,12,21,39]
Output: 8

Note:

1. 1 <= A.length <= 20000
2. 1 <= A[i] <= 100000

class Solution {
    public int largestComponentSize(int[] A) {
        int N = A.length;
        
        ArrayList<Integer>[] factored = new ArrayList[N];
        for (int i = 0; i < N; ++i) {
            factored[i] = new ArrayList<Integer>();
            int d = 2, x = A[i];
            while (d * d <= x) {
                if (x % d == 0) {
                    while (x % d == 0) 
                        x /= d;
                    factored[i].add(d);
                }
                d++;
            }
            if (x > 1 || factored[i].isEmpty())
                factored[i].add(x);
        }
        
        Set<Integer> primes = new HashSet();
        for (List<Integer> facs : factored) 
            for (int x : facs)
                primes.add(x);
        
        int[] primesL = new int[primes.size()];
        int t = 0;
        for (int x : primes)
            primesL[t++] = x;
        
        Map<Integer, Integer> primeToIndex = new HashMap();
        for (int i = 0; i < primesL.length; ++i) {
            primeToIndex.put(primesL[i], i);
        }
        
        DSU dsu = new DSU(primesL.length);
        for (List<Integer> facs : factored)
            for (int x : facs)
                dsu.union(primeToIndex.get(facs.get(0)), primeToIndex.get(x));
        
        int[] count = new int[primesL.length];
        for (List<Integer> facs : factored)
            count[dsu.find(primeToIndex.get(facs.get(0)))]++;
        
        int ans = 0;
        for (int x : count) 
            if (x > ans)
                ans = x;
        return ans;
    }
    
}

class DSU {
    int[] parent;
    public DSU(int N) {
        parent = new int[N];
        for (int i = 0; i < N; ++i) {
            parent[i] = i;
        }
    }
    
    public int find(int x) {
        if (parent[x] != x) 
            parent[x] = find(parent[x]);
        return parent[x];
    }
    
    public void union(int x, int y) {
        parent[find(x)] = find(y);
    }
}

　　

To be honset, I can't understand it.