【排序】三种经典高效排序算法

（一）快速排序

第一步：选择轴值，选择策略

第二步：将待排序序列划分为两个子序列L和R，使得L中的所有记录都小于等于轴值，而R中的所有记录都大于轴值，也就是关键的划分算法。

第三步：对子序列L和R递归快速排序。

class Solution {
    //快速排序
    public int[] sortArray(int[] nums) {
        if(nums==null ||nums.length<2)
            return nums;
        quickSort(nums,0,nums.length-1);
        return nums;
    }
    public void quickSort(int[] nums,int low,int high){
        if(low>=high)
            return;
        int index=partition(nums,low,high);
        quickSort(nums,low,index-1);
        quickSort(nums,index+1,high);
    }
    public int partition(int[] nums,int low,int high){
        int i=low,j=high;
        int temp=nums[low];  //轴值选择最左边的一个
        while(i<j){
            while(i<j && nums[j]>=temp)
                j--;
            if(i<j){
                nums[i]=nums[j];
                i++;
            }
            while(i<j && nums[i]<temp)
                i++;
            if(i<j){
                nums[j]=nums[i];
                j--;
            }
        }
        nums[i]=temp;
        return i;
    }
}

（二）归并排序

二路归并：

class Solution {
    //归并排序
    public int[] sortArray(int[] nums) {
        if(nums==null && nums.length<2)
            return nums;
        mergeSort(nums,0,nums.length-1);
        return nums;
    }
    public void mergeSort(int[] nums,int low,int high){
        if(low>=high)
            return ;
        int mid=low+(high-low)/2;
        mergeSort(nums,low,mid);
        mergeSort(nums,mid+1,high);
        merge(nums,low,mid,high);
    }
    public void merge(int[] nums, int low,int mid,int high){
        int[] temp=new int[high-low+1];
        int i=low,j=mid+1,k=0;
        while(i<=mid && j<=high){
            if(nums[i]<=nums[j])
                temp[k++]=nums[i++];
            else
                temp[k++]=nums[j++];
        }
        while(i<=mid)
            temp[k++]=nums[i++];
        while(j<=high)
            temp[k++]=nums[j++];
        
        for(int t=0;t<temp.length;t++)
            nums[t+low]=temp[t];
    }
}

（三）堆排序

堆：

  一个关键字序列｛K0，K1，…，Kn-1｝，当满足条件（1）或（2）时就称为堆。

(1) Ki ≤K2i +1 或 (2) Ki ≥K2i+1

​ Ki ≤K2i+2      Ki ≥K2i+2

  满足（1）的序列为最小堆（小顶堆）。

  满足（2）的序列为最大堆（大顶堆）。

筛选法：

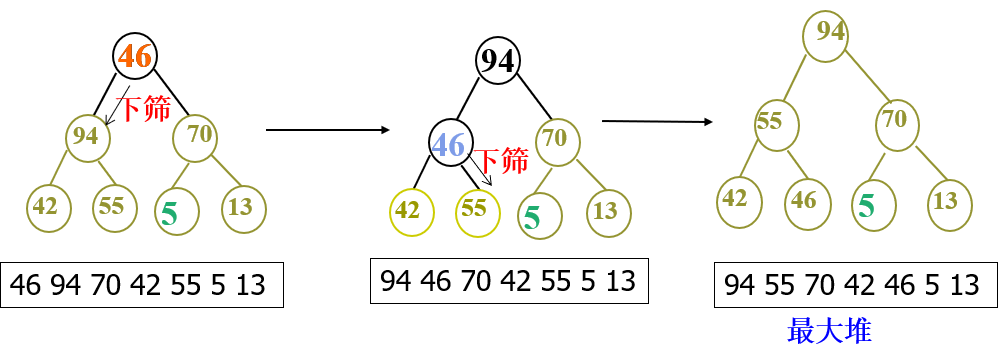
堆排序：

class Solution {
    //堆排序，O(nlogn)
    public int[] sortArray(int[] nums) {
        buildHeap(nums);  //建立初始堆
        for(int i=nums.length-1;i>=0;i--){
            //交换
            int temp=nums[0];
            nums[0]=nums[i];
            nums[i]=temp;

            //重新构建大顶堆，0下筛
            heapAdjustDown(nums,i,0);
        }

        return nums;
    }

    public void buildHeap(int[] nums){  //建堆
        for(int i=nums.length/2-1;i>=0;i--)
            heapAdjustDown(nums,nums.length,i);
    }
	
    //下筛算法，时间复杂度O(nlogn)
    public void heapAdjustDown(int[] nums, int n, int h){  //筛选算法，下筛,将nums[h]拉下来
        int i=h,temp=nums[h];  //标记父结点
        int j=2*i+1; //左孩子

        while(j<n){
            if(j<n-1 && nums[j+1]>nums[j])
                j=j+1;  //j为孩子中的较大者
            
            if(temp>nums[j])  //满足大顶堆
                break;
            else{
                nums[i]=nums[j];
                i=j;
                j=2*i+1;
            }
        }
        nums[i]=temp;
    }
}