主宰全球的十大算法:
- 归并排序、快速排序、堆排序
- 傅立叶变换和快速傅立叶变换
- 迪杰斯特拉算法(Dijkstra’s algorithm)
- RSA非对称加密算法
- 哈希安全算法(Secure Hash Algorithm)
- 整数质因子分解算法(Integer factorization)
- 链接分析算法(Link Analysis)
- 比例微积分算法
- 数据压缩算法
- 随机数生成算法
三种简单排序算法(时间复杂度O(n^2))
(一)直接插入排序
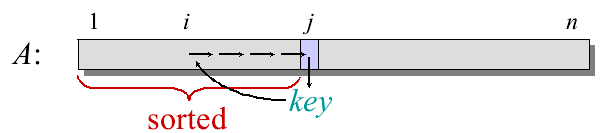
依次将每个记录插入到一个已排好序的子文件的合适位置中,插入后的文件仍然有序。稳定的排序算法,时间复杂度O(n^2)。
class Solution {
//直接插入排序
public int[] sortArray(int[] nums) {
int temp=0;
for(int i=0;i<nums.length-1;i++){
temp=nums[i+1]; //暂存第i+1个值,将其插入合适的位置
int j=i;
while(j>=0 && nums[j]>temp){
nums[j+1]=nums[j];
j--;
}
nums[j+1]=temp;
}
return nums;
}
}
(二)直接选择排序
不稳定的排序算法,在所有的记录中选出关键字最小的记录,把它与第一个记录交换存储位置,然后,再在余下的记录中选出关键字最小的记录与第二个记录交换存储位置。依此类推,直至所有的记录成为有序序列。(进行n-1趟排序)
class Solution {
//直接选择排序
public int[] sortArray(int[] nums) {
for(int i=0;i<nums.length;i++){ //选第i大的元素放到第i个位置
int small=i;
for(int j=i+1;j<nums.length;j++){
if(nums[j]<nums[small])
small=j;
}
if(small!=i)
swap(nums,i,small);
}
return nums;
}
public void swap(int[] nums,int i,int j){
int temp=nums[i];
nums[i]=nums[j];
nums[j]=temp;
}
}
(三)冒泡排序
思路:不停地比较相邻的两个记录,如果不满足排序要求,就交换相邻记录,直到第n-1个记录与第n个记录进行比较、交换后为止,完成一趟冒泡排序,使得关键字最大的记录被安置在最后一个位置上。然后,对前n-1个记录进行同样的操作,直到进行了n-1趟。
class Solution {
//冒泡排序,O(n^2)
public int[] sortArray(int[] nums) {
int flag=1;
for(int i=1;i<nums.length && flag==1;i++){ //循环n-1次
flag=0;
for(int j=0;j<nums.length-i;j++){
if(nums[j]>nums[j+1]){
flag=1;
swap(nums,j,j+1);
}
}
}
return nums;
}
public void swap(int[] nums,int i,int j){
int temp=nums[i];
nums[i]=nums[j];
nums[j]=temp;
}
}
三种简单排序算法的比较
| 直接插入排序 | 直接选择排序 | 冒泡排序 | ||||
|---|---|---|---|---|---|---|
| 关键字比 较次数 | 记录移 动次数 | 关键字比 较次数 | 记录移 动次数 | 关键字比 较次数 | 记录移 动次数 | |
| 最好(正序) | O(n) | O(n) | O(n2) | 0 | O(n) | 0 |
| 最坏(逆序) | O(n2) | O(n2) | O(n2) | O(n) | O(n2) | O(n2) |
| 平均值 | O(n2) | O(n2) | O(n2) | O(n) | O(n2) | O(n2) |
| 平均时间复杂度 | O(n2) | O(n2) | O(n2) | |||
| 空间复杂度 | O(1) | O(1) | O(1) |