教学班级:006,周五上午3、4节班。
项目地址:https://github.com/gzhGit/personalwork1.git
psp表格:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 90 | 120 |
| · Design Spec | · 生成设计文档 | 60 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 10 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 10 |
| · Design | · 具体设计 | 90 | 100 |
| · Coding | · 具体编码 | 240 | 300 |
| · Code Review | · 代码复审 | 30 | 20 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 180 | 240 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 30 | 30 |
| · Size Measurement | · 计算工作量 | 30 | 40 |
| · Postmortem & Process Improvement Plan | · 事后总结,并提出过程改进计划 | 30 | 20 |
解题思路:
- 拿到题目,构思如下:几何对象分两类——直线和圆,读一行几何参数生成一个几何对象。设置一个存储几何对象的vector,将刚生成的几何对象与vector中存储的之前生成的几何对象,输入一个负责计算的类,该类内置三个方法:计算直线与直线的交点、计算直线和圆的交点、计算圆和圆的交点。三个方法均返回内置坐标的交点对象,把交点放入set中,避免重复。当该几何对象与之前生成的所有几何对象一一计算完成后,将其存入vector中。
- 核心的部分在于计算类的实现。在网上可以找到计算直线交点、直线与圆的交点、圆和圆的交点公式,表示几何对象的参数无非是以下几种:特殊直线标志s,斜率k,截距c,圆心坐标(a,b),半径r。通过以上几个参数,可以得到几何对象的方程形式,并通过联立求解、判断特殊情况(如直线平行)等方式计算出交点坐标,或者返回一个特殊的值,表示不存在交点。
实现过程:
- 类:两种几何对象分别设置类:Line,内部包含斜率k(double)、截距c(double)、特殊标志s(int);Circle,内部包含圆心坐标(a(int),b(int))、半径r(int)。为了使两种几何对象可以统一表示,设置几何对象类Object,内部包含Line和Circle对象的指针,以及一个标志来表示其内部的两个指针哪个是有效的,以此实现Object类的二重性。设置表示交点的类Node,包含无交点标志judge(int)、x坐标x(double)、y坐标y(double)。设置负责计算的类Intersect,输入几何对象,返回包含1或2个Node对象的vector。若无交点,则置judge为1。
- 单元测试:由于计算集中在Intersect类,其他类只具有一些内置属性,所以单元测试对Intersect类的三个计算交点的方法进行测试。测试代码实现了对三个计算函数的全部分支覆盖,部分单元测试代码如下:
//直线对象
Line* line1 = new Line(0, 0, 1, 1);
Line* line2 = new Line(2, 0, 2, -1123);
//圆对象
Circle* circle1 = new Circle(2, 2, 1);
Circle* circle2 = new Circle(0, 0, 3);
Circle* circle3 = new Circle(0, 0, 2);
Circle* circle4 = new Circle(10, 0, 1);
//几何对象,可表示直线或圆
Object o1(0, line1);
Object o2(1, circle1);
Object o3(1, circle2);
//主要函数测试
Intersect i;
vector<Node> v1 = i.circleCrossCircle(*(o2.circle), *(o3.circle));
vector<Node> v2 = i.lineCrossCircle(*(o1.line), *(o2.circle));
vector<Node> v3 = i.lineCrossLine(*line1, *line2);
vector<Node> v4 = i.lineCrossCircle(*line2, *circle2);
vector<Node> v5 = i.lineCrossCircle(*line2, *circle3);
vector<Node> v6 = i.lineCrossCircle(*line1, *circle4);
int size1 = v1.size();
int size2 = v2.size();
Assert::AreEqual(size1, 2);
Assert::AreEqual(size2, 2);
Assert::AreEqual((int)v3.size(), 1);
Assert::AreEqual((int)v4.size(), 2);
Assert::AreEqual((int)v5.size(), 1);
Assert::AreEqual((int)v6.at(0).judgeCross, 0);
- 单元测试的主要对象是计算类Intersect,集中测试了其内部函数lineCrossLine()、lineCrossCircle()、circleCrossCircle(),同时还测试了Object类能否正确表示。
- 以上代码是单元测试的一部分,仅对求交点的三个函数进行粗略测试。完整的单元测试代码已提交至github,测试情况包括:两直线平行、相交(由于采用斜截式存储直线,另外测试了直线与x轴垂直时,平行与相交的情况),直线(斜率存在以及与x轴垂直的两种情况)与圆相离、相切、相交,圆与圆相离、外切、相交、内切、内含,覆盖三个求交点函数的所有分支。目前代码覆盖率工具在安装过程中出现了一些问题,暂时无法得到覆盖代码的详细统计结果。
性能分析:
- 计算圆和直线、圆和圆交点坐标时,最初是统一按照一般式方程联立求解,即将直线表示为Ax+By+C=0,将圆表示为x2+Dx+y2+Ey+F=0,求出参数值,按照求根公式统一联立求解。觉得这样比较统一简便,不管两个几何对象是否有交点,或者交点有几个,只需要通过求根公带入求解即可。
- 后来思考了一下,求根公式的计算开销还是比较大的,并不是所有情况下都要通过求根公式来计算。比如通过计算直线和圆心的距离,如果大于半径就直接返回代表无交点的值即可。
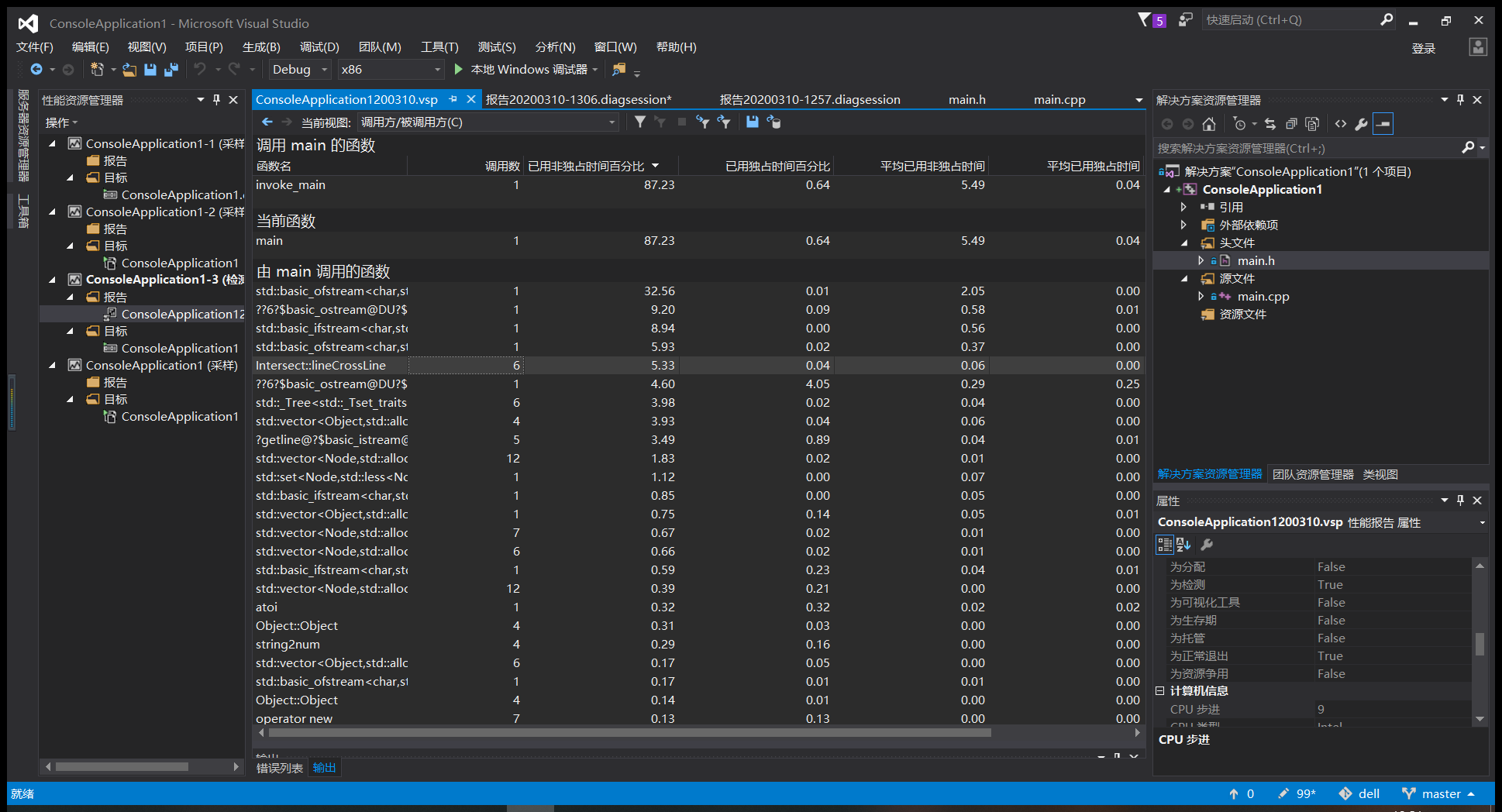
- 使用vs2015自带的性能探查器,分析项目,得到如下运行结果。由于样例规模较小,main函数调用读文件函数开销占比较大。在自定义函数中,可以在图中看出intersect类(负责计算)的lineCrossLine()开销较大,即求直线交点运算过程的耗时占比较大,性能瓶颈在于优化运算过程。
代码说明:
- 关键代码部分是从前向后遍历存储几何对象的容器,求出交点:
int count = 0;
//遍历objVector,求二者交点
for (count = 0; count < countLines; count++) {
Object objCross = objVector->at(count);
vector<Node> result; //存储几何对象交点
Intersect cal;
//当前几何对象与直线求交点
if (obj.lineOrCircle == 0) {
//直线与直线相交
if (objCross.lineOrCircle == 0) {
result = cal.lineCrossLine(*(obj.line), *(objCross.line));
}
//直线与圆相交
else if (objCross.lineOrCircle == 1) {
result = cal.lineCrossCircle(*(obj.line), *(objCross.circle));
}
}
//当前几何对象与圆求交点
else if (obj.lineOrCircle == 1) {
//圆与直线相交
if (objCross.lineOrCircle == 0) {
result = cal.lineCrossCircle(*(objCross.line), *(obj.circle));
}
//圆与圆相交
else if (objCross.lineOrCircle == 1) {
result = cal.circleCrossCircle(*(obj.circle), *(objCross.circle));
}
}
//将求解所得的交点存入nodeSet
int runover;
for (runover = 0; runover < (int)result.size(); runover++) {
Node node = result.at(runover);
if (node.judgeCross == 1) {
nodeSet->insert(node);
}
}
}
-
objVector是存储几何对象的容器,每读入一行几何参数,就生成一个几何对象,记作obj。从前向后遍历objVector,将obj与容器中的每个几何对象求解交点,其中有细分的四种情况:直线和直线求交点,直线和圆求交点,圆和直线求交点(与前者调用同一函数),圆和圆求交点。求解交点的函数返回一个存储交点的容器,检查这些交点,如果其judgeCross值为0,说明二者无交点;反之说明二者存在交点,将交点存入nodeSet中。
-
使用vs2017的运行代码分析,对项目进行检测,结果无警告。截图如下: