1. 概述
Logistic回归分析也用于研究影响关系,即X对于Y的影响情况。Y为定量数据,X可以是定量数据或定类数据。主要是研究二分类观察结果与一些影响因素之间关系的一种多变量分析方法。因变量可以是二分类的,也可以是多分类的。主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率等等,常用于数据挖掘,疾病自动诊断,经济预测等领域。
在书中使用Logistic回归来预测患疝气病的马的存活问题是一个典型的案例,项目数据集包含了医院检测马疝病的368个样本和28个特征,有的指标比较主观,有的指标难以测量。
Logistic回归和线性回归最大的区别在于,Y的数据类型。线性回归分析的因变量Y属于定量数据,而Logistic回归分析的因变量Y属于分类数据。
2. 算法
线性回归中,主要是采用最小二乘法进行参数估计,使其残差平方和最小。同时在线性回归中最大似然估计和最小二乘法估计结果是一致的,但不同的是最大似然估计可以用于非线性模型,又因为逻辑回归是非线性模型,所以逻辑回归最常用的估计方法是最大似然法。
最大似然法基本思想:
当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大,而不是像最小二乘估计法旨在得到使得模型能最好地拟合样本数据的参数估计量。
3. 分类
Logistic回归在进一步细分,又可分为二元Logit(Logistic)回归、多分类Logit(Logistic)回归,有序Logit(Logistic)回归。
4. 抛砖
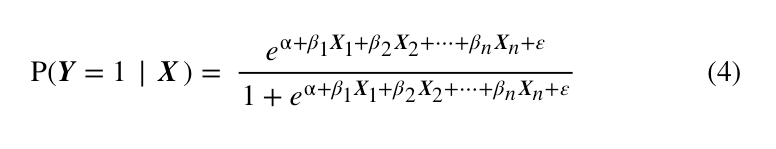
至此,我们回归方程构建的任务算是完成了。下面就是找到一个更简单的方式来表示上式,使公式看起来更像一个回归方程。
事实上,这一步很简单,只需要经过简单的变换,则可以得到下式:
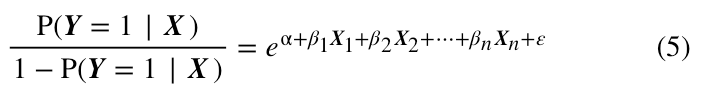
再将上式的左右两边同时取对数,则得到:
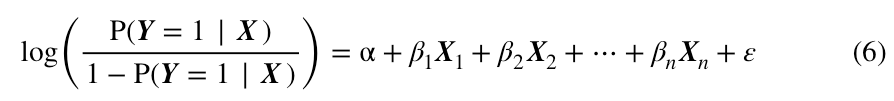
如你所见,上式中,至少右边已经完全是普通回归方程的结构了,至于左边,我们再来解释。
在等式左边,是Y出现阳性结果的概率,自然的,就是Y出现阴性结果的概率,两者的比值被叫做“比率”(odds),取对数后,自然就被叫做对数比率。所以,logistic回归在机器学习领域通常被叫做对数比率回归。
5.代码
使用Pyton3实现
''' Created on Oct 27, 2010 Logistic Regression Working Module @author: Peter ''' from numpy import * from numpy.core._multiarray_umath import exp def loadDataSet(): dataMat = []; labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineArr = line.strip().split() dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) labelMat.append(int(lineArr[2])) return dataMat,labelMat def sigmoid(inX): return 1.0/(1+exp(-inX)) def gradAscent(dataMatIn, classLabels): dataMatrix = mat(dataMatIn) #convert to NumPy matrix labelMat = mat(classLabels).transpose() #convert to NumPy matrix m,n = shape(dataMatrix) alpha = 0.001 maxCycles = 500 weights = ones((n,1)) for k in range(maxCycles): #heavy on matrix operations h = sigmoid(dataMatrix*weights) #matrix mult error = (labelMat - h) #vector subtraction weights = weights + alpha * dataMatrix.transpose()* error #matrix mult return weights def plotBestFit(weights): import matplotlib.pyplot as plt dataMat,labelMat=loadDataSet() dataArr = array(dataMat) n = shape(dataArr)[0] xcord1 = []; ycord1 = [] xcord2 = []; ycord2 = [] for i in range(n): if int(labelMat[i])== 1: xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) else: xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') ax.scatter(xcord2, ycord2, s=30, c='green') x = arange(-3.0, 3.0, 0.1) y = (-weights[0]-weights[1]*x)/weights[2] ax.plot(x, y) plt.xlabel('X1'); plt.ylabel('X2'); plt.show() def stocGradAscent0(dataMatrix, classLabels): m,n = shape(dataMatrix) alpha = 0.01 weights = ones(n) #initialize to all ones for i in range(m): h = sigmoid(sum(dataMatrix[i]*weights)) error = classLabels[i] - h weights = weights + alpha * error * dataMatrix[i] return weights def stocGradAscent1(dataMatrix, classLabels, numIter=150): m,n = shape(dataMatrix) weights = ones(n) #initialize to all ones for j in range(numIter): # 对数据重复进行150次的整体读取,即迭代150次 dataIndex = list(range(m)) # 每一次迭代,都会遍历所有的数据 for i in range(m): alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant h = sigmoid(sum(dataMatrix[randIndex]*weights)) error = classLabels[randIndex] - h weights = weights + alpha * error * dataMatrix[randIndex] del(dataIndex[randIndex]) return weights def classifyVector(inX, weights): prob = sigmoid(sum(inX*weights)) if prob > 0.5: return 1.0 else: return 0.0 def colicTest(): frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt') trainingSet = []; trainingLabels = [] for line in frTrain.readlines(): currLine = line.strip().split(' ') lineArr =[] for i in range(21): lineArr.append(float(currLine[i])) trainingSet.append(lineArr) trainingLabels.append(float(currLine[21])) trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000) # list->array errorCount = 0; numTestVec = 0.0 for line in frTest.readlines(): numTestVec += 1.0 currLine = line.strip().split(' ') lineArr =[] for i in range(21): lineArr.append(float(currLine[i])) if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]): errorCount += 1 errorRate = (float(errorCount)/numTestVec) print ("the error rate of this test is: %f" % errorRate) return errorRate def multiTest(): numTests = 10; errorSum=0.0 for k in range(numTests): errorSum += colicTest() print ("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests))) if __name__ == '__main__': multiTest()
https://blog.csdn.net/weixin_44568780/article/details/103435101
https://www.cnblogs.com/pursued-deer/p/7819539.html
以下两行代码
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
的公式推导,可以参考: