经典DFS问题实践

八皇后问题：

//八皇后问题  经典的DFS问题实践
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;
int mat[8][8];
int ans=0;
bool check(int row,int col)//最终检查满足要求，则return 1
{
    for(int i=0;i<row;i++)
    {
        if(mat[i][col])
            return false;
        for(int j=0;j<8;j++)
        {
            //不能在同一条对角线上
            if(mat[i][j])
            {
              if(fabs(i-row)-fabs(j-col)==0)
                 return 0;
              else
                 continue;

            }
        }
    }
    return 1;
}
int dfs(int row)
{
    if(row>=8)
    {
        ans++;
        for(int i=0;i<8;i++)
        {
            for(int j=0;j<8;j++)
               cout<<mat[i][j]<<" ";
            cout<<endl;
        }
        cout<<endl;
    }
    for(int col=0;col<8;col++)
    {
        if(check(row,col))
        {
            mat[row][col]=1;
            dfs(row+1);
            mat[row][col]=0;
        }
    }
    return 0;
}
int main()
{
    memset(mat,0,sizeof(mat));
    dfs(0);
    cout<<"一共有"<<ans<<"种解决方案"<<endl;
}

 //最终结果显示一共有92种解决方案

部分和问题

给定整数a1、a2、.......an,判断是否可以从中选出若干个数，使他们的和恰好为k。

//部分和问题
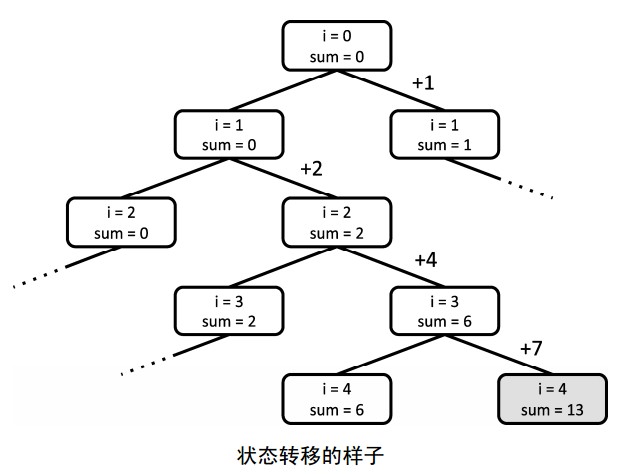
#include <iostream>
using namespace std;
const int Maxn=10000;
int a[Maxn];
int n,k;
bool dfs(int i,int sum){
    if(i==n) return sum==k;
    if(dfs(i+1,sum)) return true;//不加上a[i]的情况
    if(dfs(i+1,sum+a[i])) return true;
    return false;

}
void solve()
{
    if(dfs(0,0)) printf("yes!");
    else printf("no!");
}
int main() {
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    cin>>k;
    solve();
    return 0;
}