环形链表--链表

题目

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

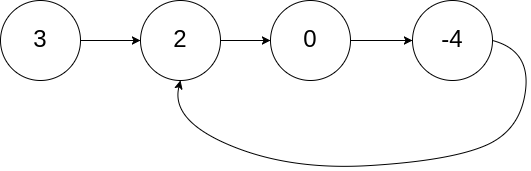
 示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

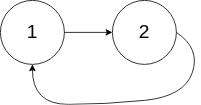
 示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

思想 

我们可以通过检查一个结点此前是否被访问过来判断链表是否为环形链表。常用的方法是使用哈希表。

我们遍历所有结点并在哈希表中存储每个结点的引用（或内存地址）。如果当前结点为空结点 null（即已检测到链表尾部的下一个结点），那么我们已经遍历完整个链表，并且该链表不是环形链表。如果当前结点的引用已经存在于哈希表中，那么返回 true（即该链表为环形链表）。

代码

public boolean hasCycle(ListNode head) {
    Set<ListNode> nodesSeen = new HashSet<>();
    while (head != null) {
        if (nodesSeen.contains(head)) {
            return true;
        } else {
            nodesSeen.add(head);
        }
        head = head.next;
    }
    return false;
}

换种思路

通过使用具有 不同速度 的快、慢两个指针遍历链表，空间复杂度可以被降低至 O(1)O(1)。慢指针每次移动一步，而快指针每次移动两步。

如果列表中不存在环，最终快指针将会最先到达尾部，此时我们可以返回 false。

现在考虑一个环形链表，把慢指针和快指针想象成两个在环形赛道上跑步的运动员（分别称之为慢跑者与快跑者）。而快跑者最终一定会追上慢跑者。这是为什么呢？考虑下面这种情况（记作情况 A）- 假如快跑者只落后慢跑者一步，在下一次迭代中，它们就会分别跑了一步或两步并相遇。

其他情况又会怎样呢？例如，我们没有考虑快跑者在慢跑者之后两步或三步的情况。但其实不难想到，因为在下一次或者下下次迭代后，又会变成上面提到的情况 A。

代码

public boolean hasCycle(ListNode head) {
    if (head == null || head.next == null) {
        return false;
    }
    ListNode slow = head;
    ListNode fast = head.next;
    while (slow != fast) {
        if (fast == null || fast.next == null) {
            return false;
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    return true;
}