导数求函数最值
本文作者@guodongLovesOi 没有将导数用法规范,如果被数学老师打作者概不负责
首先对于二次函数 (f(x)=x^2+3x+1)
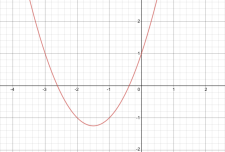
我们可以很方便的求出导数:
[ 设 riangle=lim_{ riangle->0} ,x'=x- riangle\
那么f'(x)=frac{f(x)-f(x')}{x-x'} \
即 \
frac{x^2+3x+1-{x'}^2-3x'-1}{x-x'}= \
frac{(x+x')(x-x')+3(x-x')}{x-x'}=\
即 quad{2x+3}
]
设定点为坐标为((v,f(v))),由图可知,在(f'(v)=0)
( herefore v=-frac{3}{2})
将(v) 代入:
[(-frac{3}{2},{(-frac{3}{2})}^2-3 imes frac{3}{2}+1)\
(-frac{3}{2},-frac{5}{4})
]
通过可爱的顶点式可以验算上面是对的。
那么扩展到二次函数(f(x)=ax^2+bx+c)
[ 设 riangle=lim_{ riangle->0},x'=x- riangle\
所以f(x)的导数f'(x)可以这样计算:\
frac{ax^2+bx+c-a{x'}^2-bx'-c}{x-x'}=\
frac{a(x^2-(x')^2)+b(x-x')}{x-x'}=\
frac{a(x+x')(x-x')+b(x-x')}{x-x'}=\
a(x+x')+b= \
即quad 2ax+b
]
代入上面的可爱的二次函数可以简单的验算这是正确的.
[ 2av+b=0 \
v=-frac{b}{2a} \
v(-frac{b}{2a},f(-frac{b}{2a}))
]
草,跟课本结论一样,装不了X了.
信息学部分
接下来我们来扩展到(n)次函数。(模板:三分法)
容易根据求导的过程发现
(f'(x)=frac{f(x)-f(x')}{x-x'})
但是,对于一个毒瘤的(n)次函数,我们比较难像上面那样转化
但是我们可以将某一个点具体化呀!
考虑题目中的(l,r)限制,我们只需要找出最接近(0)的那个位置就好了。
水题一道