概述
继续刷题,本篇算法主要偏向字符串和数组部分
第二十五题
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针random指向一个随机节点),请对此链表进行深拷贝,并返回拷贝后的头结点。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)
解题思路
第一种思路:下面的思路为牛客网上以为朋友给出的,这个思路挺好,不过不容易想到,我也没有想到,我是通过使用map实现的。
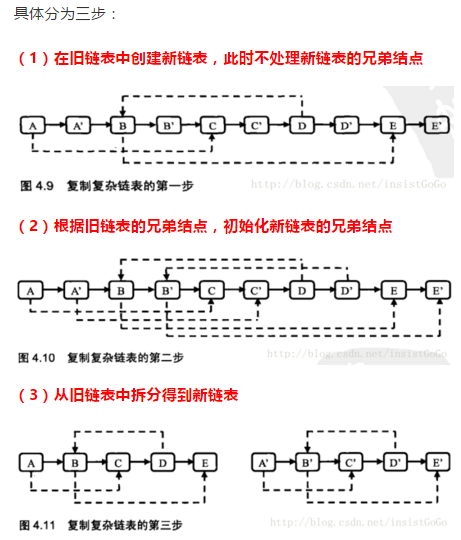
第二种思路:把链表中每一个节点都保存在map中,做好源节点和拷贝节点的映射,就很容易解决。
代码
import java.util.Map; import java.util.HashMap; public class Solution { public RandomListNode Clone(RandomListNode pHead){ RandomListNode node = pHead; Map<RandomListNode,RandomListNode> map = new HashMap(); while(node != null){ RandomListNode newNode = new RandomListNode(node.label); map.put(node,newNode); node = node.next; } RandomListNode node1 = pHead; while(node1 != null){ RandomListNode newNode = map.get(node1); newNode.next = map.get(node1.next); newNode.random = map.get(node1.random); node1 = node1.next; } return map.get(pHead); } }
第二十六题
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
解题思路:这个题其实通过中序遍历这颗二叉树,就可以实现题中要求的排序功能,因为这个二叉树是一个二叉搜索树,至于改成一个双向链表,这个只要改一下指针的方向就可以了。
代码
/** public class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } */ import java.util.Stack; public class Solution { public TreeNode Convert(TreeNode pRootOfTree) { if(pRootOfTree == null){ return null; } Stack<TreeNode> stack = new Stack(); stack.add(pRootOfTree); TreeNode temp = pRootOfTree; TreeNode temp1 = null; TreeNode root = null; TreeNode temp2 = null; while(!stack.isEmpty()){ if(temp != null && temp.left != null){ stack.push(temp.left); temp = temp.left; }else{ temp = stack.pop(); temp.left = temp1; //temp2 = temp; if(temp1 != null){ temp1.right = temp; }else{
//记录头结点 root = temp; } temp1 = temp; if(temp.right != null){ stack.push(temp.right); temp = temp.right; }else{ temp = null; } } } return root; } }
第二十七题
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则按字典序打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
解题思路:这个题其实要做出来很容易,难的是怎么使用最低的时间复杂度做出来,我之前想过一种思路,具体的做法如下:
第一步:从头开始,让a,分别和b,c交换,结果为bac,bca
第二步:依然从头开始,这时的字符串是bca,经过交换之后可以获得cba,cab
第三步:重复以上过程获得acb,abc,大家可以发现经过上面的过程abc又变成了abc,是不是很神奇
第二种思路,这个思路来自于牛客网,使用递归来实现
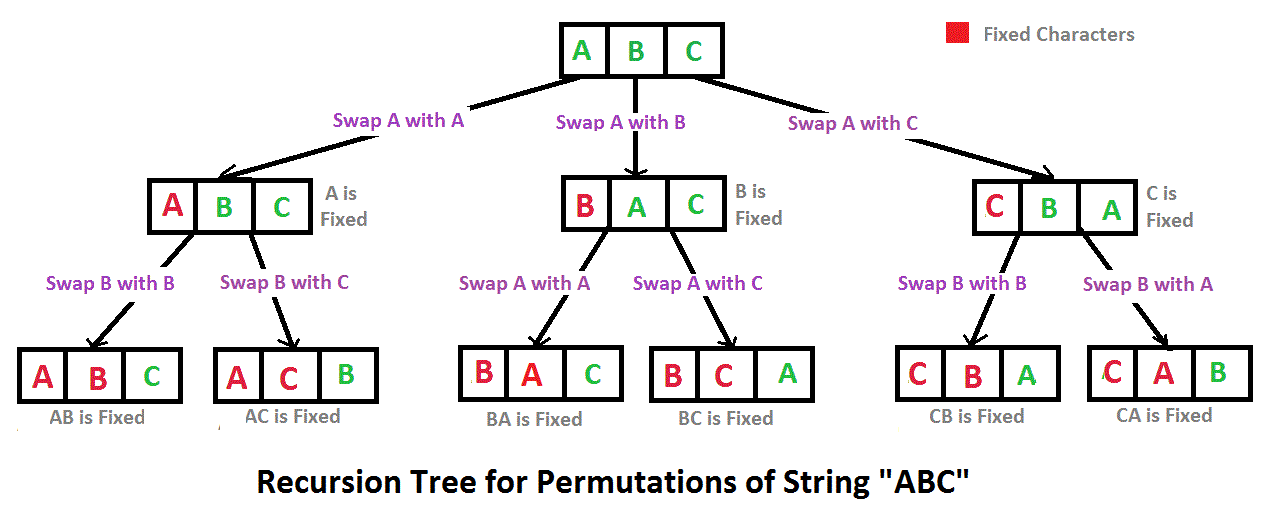
这个思路的递归是怎么用的呢?如下
第一步:先固定好第一个字母,比如字符串中有5个不同的字符,那第一次就要把字符串分成5中情况
第二步:有了第一步之后,相当于第一个字母已经搞定了,那就搞定第二个字母,让他也有这么多种的排列组合
。。。
第n步:直到最后一个字母
总结:通过递归的方式思路很容易明白,但是代码写起来没有那么容易,通过我想的那种方式我觉得挺好,时间复杂度也挺好。
代码
public class AllCombinationString { public static String str = "abcd"; public static void allCombination(){ char[] chars = str.toCharArray(); //防止字符串中有重复字符导致相同的组合 Set<String> set = new HashSet<>(); //思路就是每次从头开始交换,第一个元素和第二个,然后和第三个元素交换 //当所有的交换一遍之后,就把所有可能的结果拿到了 for (int i = 0; i < chars.length; i++) { int j=0; while(j+1 < chars.length){ swap(chars,j,j+1); set.add(String.valueOf(chars)); j++; } } for (String s:set) { System.out.println(s); } } public static void swap(char[] array, int i, int j){ if (i == j){ return; } char temp = array[i]; array[i] = array[j]; array[j] = temp; } public static void main(String[] args) { allCombination(); } }
第二十八题
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
解题思路:这个题我是使用了最简单的实现方式,就是统计每个数字出现的次数,然后看哪个超过一半,有点原始,不过我觉得思路很清晰。
代码
import java.util.Map; import java.util.HashMap; public class Solution { public int MoreThanHalfNum_Solution(int [] array) { if (array.length == 1){ return array[0]; } Map<Integer,Integer> map = new HashMap(); Integer temp; for(int i = 0;i< array.length;i++){ temp = map.get(array[i]); if(temp == null){ map.put(array[i],1); }else{ if(temp+1 > array.length/2){ return array[i]; } map.put(array[i],temp+1); } } return 0; } }
第二十九题
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4。
解题思路:看牛客网上思路最多的就是把k个数放到list中,然后遍历数据,每次和list中的最大的数进行比较,如果大于这个数,不处理,如果小于list中的最大数,那就需要把最大的数给替换掉,这个思路最大的开销就是每次都要找list中的最大数,时间复杂度相当于O(nk),我使用了一种优化的方式,先把list排好序,list中采用二分查找法,把每个数字放到list中的正确位置,保证list一直是有序的
代码
import java.util.ArrayList; public class Solution { public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) { ArrayList<Integer> list = new ArrayList(); if(k <= 0 || k > input.length){ return list; } for(int i = 0;i < k;i++){ list.add(i,input[i]); } list.sort((o1,o2)-> o1-o2); for(int j = k;j<input.length;j++){ if(input[j] >= list.get(k-1)){ continue; }else{
//使用二分查找法找到这个数在列表中的相对位置 int result = binarySearch(list,input[j]);
//把列表中的最后一个元素移除,最后一个是最大的元素 list.remove(k-1); list.add(result,input[j]); } } return list; } //这段代码写的太长了,其实二分查找发一般由于判断在数组中是否存在这个数,判断位置就比较麻烦了 public static int binarySearch(ArrayList<Integer> list, int value){ int start = 0; int end = list.size()-1; int mid = end/2; while(end>=start){ if(end == start){ if (list.get(start) < value){ return start+1; } return start; } if(value > list.get(mid)){ start = mid + 1; if (start > end){ return end; } }else if(value < list.get(mid)){ end = mid - 1; if (end < start){ return start; } }else{ return mid; } mid = (start + end)/2; } return -1; } }
第三十题
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,
问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。
给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
解题思路:这道题是求数组的子数组元素的最大和,在牛客网上看到一个牛逼的解决办法,就是如果遇见的是负数,就找负数中最大的,如果是正数就加和,其实我自己的实现也是这个思路,不过我的实现太过复杂。
代码
大佬的实现
链接:https://www.nowcoder.com/questionTerminal/459bd355da1549fa8a49e350bf3df484 来源:牛客网 public class Solution { public int FindGreatestSumOfSubArray(int[] array) { if (array.length==0 || array==null) { return 0; } int curSum=0; int greatestSum=0x80000000; for (int i = 0; i < array.length; i++) { if (curSum<=0) { curSum=array[i]; //记录当前最大值 }else { curSum+=array[i]; //当array[i]为正数时,加上之前的最大值并更新最大值。 } if (curSum>greatestSum) { greatestSum=curSum; } } return greatestSum; } }
我的实现

import java.util.ArrayList; public class Solution { public int FindGreatestSumOfSubArray(int[] array) { if(array == null || array.length == 0){ return 0; } ArrayList<Integer> list = new ArrayList(); int sum = 0; int z = 0; int f = 0; int fMin = array[0]; for(int i = 0;i < array.length;i++){ //标记从正数开始还是从负数开始 if(z == 0 && f == 0){ if(array[i] < 0){ if (array[i] > fMin){ fMin = array[i]; } if (i == array.length-1){ list.add(fMin); } continue; } } if(array[i] > 0){ if( f == 0){ z = z + array[i]; if (i == array.length-1){ list.add(sum + z); } }else{ list.add(sum+z); if(z + f > 0){ sum = sum + z + f; }else{ sum = 0; } z = array[i]; f = 0; } }else{ f = f + array[i]; if (i == array.length-1){ list.add(sum + z); } } } Integer max = list.get(0); for(int i = 0;i < list.size();i++){ if(list.get(i) > max){ max = list.get(i); } } return max; } }
第三十一题
求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数?为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。
ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数(从1 到 n 中1出现的次数)。
解题思路:这个题很简单,就不说了
代码
import java.lang.String; public class Solution { public int NumberOf1Between1AndN_Solution(int n) { int count = 0; char flag = '1'; for(int i = 1;i <= n;i++){ for(char c:String.valueOf(i).toCharArray()){ if(c == flag){ count++; } } } return count; } }
第三十二题
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组{3,32,321},则打印出这三个数字能排成的最小数字为321323。
解题思路:这个题在牛客上看到一个很强的解题思路,一开始我想这个的时候,觉得要自己写一个while循环,一个一个元素互相比较,找出字符排列中最符合要求的,然后这样就可以实现最小的组合,但是这样一轮循环只能找到一个合适的元素,这个时间复杂度是n*(n-1)*(n-2)...1,然后我看到牛客上有人通过使用List集合自带的排序方法sort来实现的,其实排序也是两两比较,时间复杂度是nlog(n)
代码
import java.util.ArrayList; import java.util.Arrays; public class Solution { public static String PrintMinNumber(int [] numbers) { StringBuilder result = new StringBuilder(); String[] str = new String[numbers.length]; for (int i = 0; i < numbers.length; i++) { str[i] = String.valueOf(numbers[i]); } Arrays.sort(str,(o1,o2)->{ String temp1 = o1 + "" + o2; String temp2 = o2 + "" + o1;
//String实现了compareTo方法,会比较对应字符的大小 return temp1.compareTo(temp2); }); for (int i = 0; i < str.length; i++) { result.append(str[i]); } return result.toString(); } }
总结
链表和树部分的题感觉偏难,数组和字符串部分的题觉得相对来说容易一些
