1、什么是Numpy
numpy官方文档:https://docs.scipy.org/doc/numpy/reference/?v=20190307135750
NumPy是一个功能强大的Python库,主要用于对多维数组执行计算。NumPy这个词来源于两个单词-- Numerical和Python。
它是 Python 生态系统中数据分析、机器学习和科学计算的主力军。它极大地简化了向量和矩阵的操作处理。Python 数据科学相关的一些主要软件包(如 scikit-learn、SciPy、pandas 和 tensorflow)都以 NumPy 作为其架构的基础部分。除了能对数值数据进行切片(slice)和切块(dice)之外,使用 NumPy 还能为处理和调试上述库中的高级实例带来极大便利组。它将常用的数学函数都支持向量化运算,使得这些数学函数能够直接对数组进行操作,将本来需要在Python级别进行的循环,放到C语言的运算中,明显地提高了程序的运算速度。
2、为什么要用Numpy
NumPy是Python中的一个运算速度非常快的一个数学库,它非常重视数组。它允许你在Python中进行向量和矩阵计算,并且由于许多底层函数实际上是用C编写的,因此你可以体验在原生Python中永远无法体验到的速度。
import numpy as np
import time
# 用python自带方法处理
def func(values):
result = []
for v in values:
result.append(v * v)
return result
data = range(10000)
%timeit func(data)
运行结果:
1.07 ms ± 20.5 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
# 用numpy中的方法处理
arr = np.arange(0,10000)
%timeit arr ** arr
运行结果:
397 µs ± 32.5 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
NumPy绝对是科学Python成功的关键之一,如果你想要进入Python中的数据科学或机器学习,你就要必须学习它。从最后的执行结果来看numpy的处理速度要比python的处理速度快上十几倍,当然这只是它的其中一项优势,下面就通过一些具体的操作来看一看numpy的用法与优势。
3、怎么用Numpy
安装方法:
pip install numpy
引用方式:
import numpy as np
这是官方认证的导入方式,可能会有人说为什么不用from numpy import *,是因为在numpy当中有一些方法与Python中自带的一些方法,例如max、min等冲突,为了避免这些麻烦大家就约定俗成的都使用这种方法。
Numpy的核心特征就是N-维数组对——ndarray.
3.1、为什么要用ndarray?
numpy所有的操作都是围绕着数组展开的,这个数组的名字就叫做ndarray,在学习ndarray数组之前肯定有人会说这个东西和Python中的列表差不多啊,为什么不用列表呢,列表还要方便些。其实列表list本身是为了处理更广泛、更通用的目的而构建的,其实从这一方面来看ndarray对于处理这个数组类型结构的数据会更加方便。
接下来我们可以通过具体的实例来展示一下ndarray的优势。
现在有这样一个需求:
已知若干家跨国公司的市值(美元),将其换算为人民币
按照Python当中的方法
第一种:是将所有的美元通过for循环依次迭代出来,然后用每个公司的市值乘以汇率
第二种:通过map方法和lambda函数映射
这些方法相对来说也挺好用的,但是再来看通过ndarray对象是如何计算的
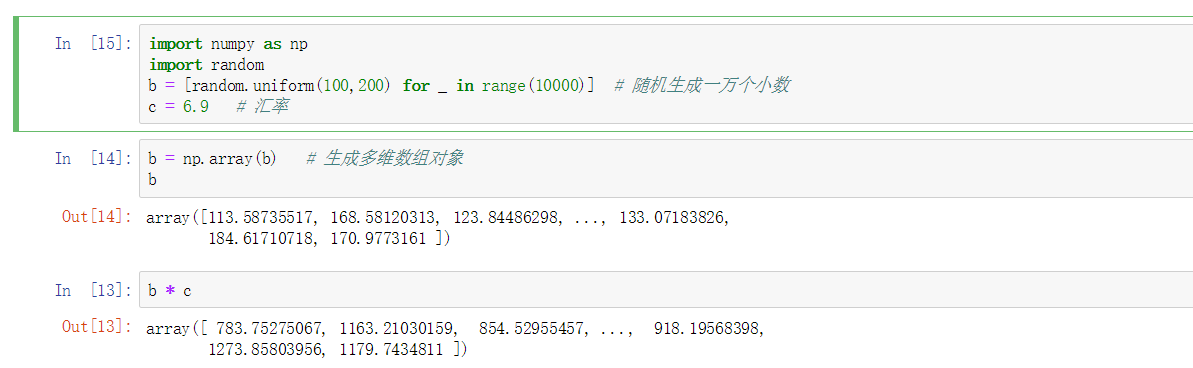
通过ndarray这个多维数组对象可以让这些批量计算变得更加简单,当然这只它其中一种优势,接下来就通过具体的操作来发现。
3.2、ndarray-创建
| 方法 | 描述 |
|---|---|
| array() | 将列表转换为数组,可选择显式指定dtype |
| arange() | range的numpy版,支持浮点数 |
| linspace() | 类似arange(),第三个参数为数组长度 |
| zeros() | 根据指定形状和dtype创建全0数组 |
| ones() | 根据指定形状和dtype创建全1数组 |
| empty() | 根据指定形状和dtype创建空数组(随机值) |
| eye() | 根据指定边长和dtype创建单位矩阵 |

1、arange():
np.arange(1.2,10,0.4)
执行结果:
array([1.2, 1.6, 2. , 2.4, 2.8, 3.2, 3.6, 4. , 4.4, 4.8, 5.2, 5.6, 6. ,
6.4, 6.8, 7.2, 7.6, 8. , 8.4, 8.8, 9.2, 9.6])
# 在进行数据分析的时候通常我们遇到小数的机会远远大于遇到整数的机会,这个方法与Python内置的range的使用方法一样
-----------------------------------------------------------------
2、linspace()
np.linspace(1,10,20)
执行结果:
array([ 1. , 1.47368421, 1.94736842, 2.42105263, 2.89473684,
3.36842105, 3.84210526, 4.31578947, 4.78947368, 5.26315789,
5.73684211, 6.21052632, 6.68421053, 7.15789474, 7.63157895,
8.10526316, 8.57894737, 9.05263158, 9.52631579, 10. ])
# 这个方法与arange有一些区别,arange是顾头不顾尾,而这个方法是顾头又顾尾,在1到10之间生成的二十个数每个数字之间的距离相等的,前后两个数做减法肯定相等
----------------------------------------------------------------
3、zeros()
np.zeros((3,4))
执行结果:
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
# 会用0生成三行四列的一个多维数组
---------------------------------------------------------------------
4、ones()
np.ones((3,4))
执行结果:
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
# 会用1生成三行四列的一个多维数组
------------------------------------------------------------------------
5、empty()
np.empty(10)
执行结果:
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
# 这个方法只申请内存,不给它赋值
-----------------------------------------------------------------------
6、eye()
np.eye(5)
执行结果:
array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
# 对角矩阵
3.3、ndarray是一个多维数组列表
接下来就多维数组举个例子:
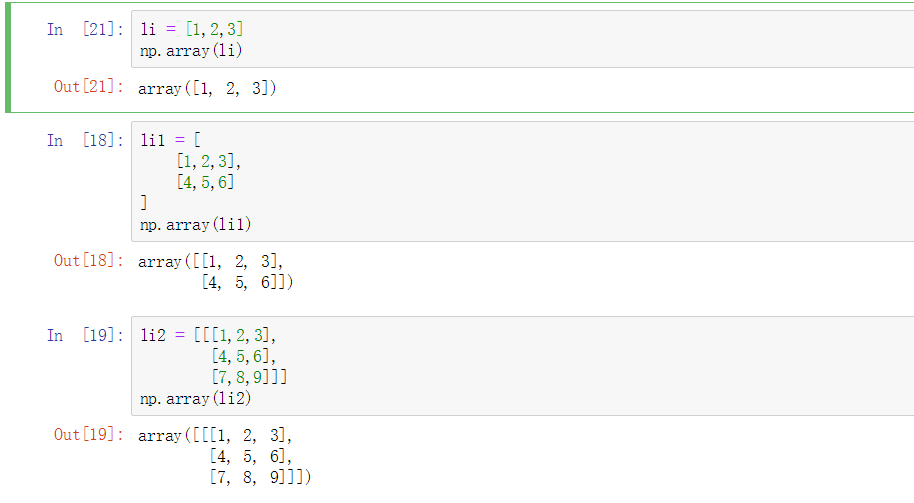
为了创建一个2维数组,我们是传递了一个列表的列表给这个array()函数。如果我们想要的是一个三维数组,我们就必须要一个列表的列表的列表(也就是三层列表),以此类推。

很多情况下,处理一个新的维度只需要在numpy函数的参数中添加一个逗号
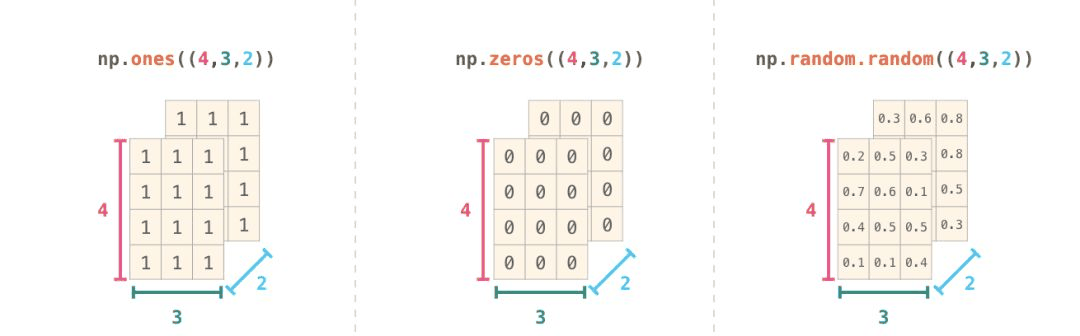
有的人可能会说了,这个数组跟Python中的列表很像啊,它和列表有什么区别呢?
'''
在python中列表是可以存任意类型的值的,但是在数组当中的元素必须类型必须相同。这是因为列表中存的只是每个元素的地址,不管运行多少次,值的位置是不会改变的,不需要在意数据的类型;而在ndarray当中存的是具体的值,每一次执行都是重新存放。
'''
l1 = ['1','2',4]
na = np.array(l1)
print(f"ndarry:{id(na[0])}")
print(f"list:{id(l1[0])}")
> ndarry:2140960887632
list:2140897577592
"""
通过多次执行其实就可以发现,ndarray数组的id值一直在不停的换,而list的id值始终保持不变
"""
- 数组对象内的元素类型必须相同
- 数组大小不可修改
3.4、常用属性
| 属性 | 描述 |
|---|---|
| T | 数组的转置(对高维数组而言) |
| dtype | 数组元素的数据类型 |
| size | 数组元素的个数 |
| ndim | 数组的维数 |
| shape | 数组的维度大小(以元组形式) |
| itemsize | 每个项占用的字节数 |
| nbytes | 数组中的所有数据消耗掉的字节数 |
# T:转置 转置是一种特殊的数据重组形式,可以返回底层数据的视图而不需要复制任何内容。
# 通俗点说,转置就是将数据旋转90度,行变成列,列变成行。
li1 = [
[1,2,3],
[4,5,6]
]
a = np.array(li1)
a.T
执行结果:
array([[1, 4],
[2, 5],
[3, 6]])

# dtype:返回当前数据的数据类型
arr = np.arange(10)
arr.dtype
执行结果:
dtype('int32')
# size:返回当前数组内存在的元素个数
l1 = [[[1,2,3],
[4,5,6]],
[[7,8,9],
[1,5,9]
]]
arr1 = np.array(l1)
arr1.size
执行结果:
12
# ndim:返回当前数组维度
l1 = [[[1,2,3],
[4,5,6]],
[[7,8,9],
[1,5,9]
]]
arr1 = np.array(l1)
arr1.ndim
执行结果:
3
# shape:返回数组维度大小
l1 = [[[1,2,3,4],
[4,5,6,5],
[6,8,3,6]],
[[7,8,9,7],
[1,5,9,7],
[4,6,8,4]
]]
arr1 = np.array(l1)
arr1.shape
执行结果:
(2, 3, 4)
"""
最终三个参数代表的含义依次为:二维维度,三维维度,每个数组内数据大小
要注意这些数组必须要是相同大小才可以
"""
3.5、数据类型
- dtype
| 类型 | 描述 |
|---|---|
| 布尔型 | bool_ |
| 整型 | int_ int8 int16 int32 int 64 |
| 无符号整型 | uint8 uint16 uint32 uint64 |
| 浮点型 | float_ float16 float32 float64 |
整型:
int32只能表示(-2**31,2**31-1),因为它只有32个位,只能表示2**32个数
无符号整型:
只能用来存正数,不能用来存负数
"""
补充:
astype()方法可以修改数组的数据类型
示例:
data.astype(np.float)
"""
3.6、向量化数学运算
- 数组和标量(数字)之间运算
li1 = [
[1,2,3],
[4,5,6]
]
a = np.array(li1)
a * 2
运行结果:
array([[ 2, 4, 6],
[ 8, 10, 12]])

与标量之间进行向量化运算,多维数组与一维数组没有任何区别,都会将你要运算的数字映射到数组中的每一个元素上进行运算
- 同样大小数组之间的运算
# l2数组
l2 = [
[1,2,3],
[4,5,6]
]
a = np.array(l2)
# l3数组
l3 = [
[7,8,9],
[10,11,12]
]
b = np.array(l3)
a + b # 计算
执行结果:
array([[ 8, 10, 12],
[14, 16, 18]])

数组与数组之间的向量化运算,两个运算的数组必须相同大小,否则会报错
3.7、索引和切片
- 索引
一维索引使用与python本身的列表没有任何区别,所以接下来主要针对大的是多维数组
# np重塑
arr = np.arange(30).reshape(5,6) # 后面的参数6可以改为-1,相当于占位符,系统可以自动帮忙算几列
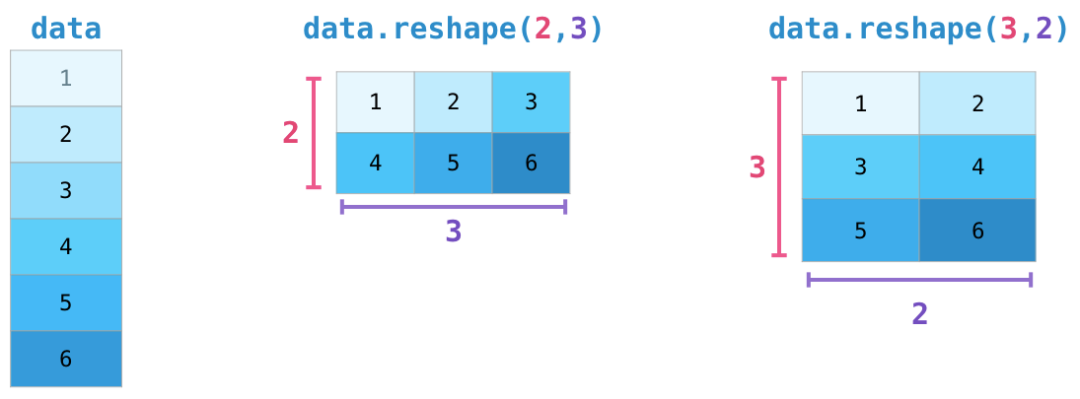
# 将二维变一维
arr.reshape(30)
# 索引使用方法
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29]])
现在有这样一组数据,需求:找到20
列表写法:arr[3][2]
数组写法:arr[3,2] # 中间通过逗号隔开就可以了
- 切片
arr数组
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29]])
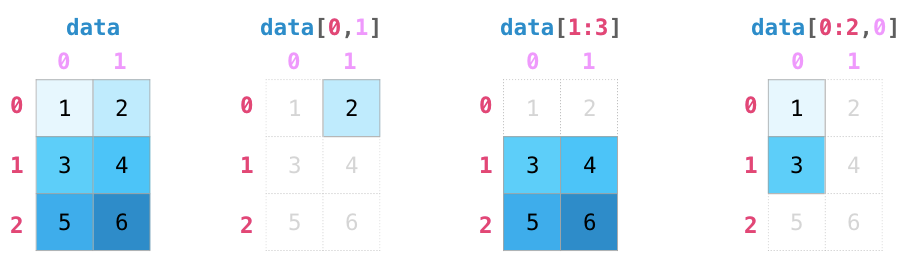
arr[0,1:4] # >>array([1, 2, 3])
arr[1:4,0] # >>array([ 6, 12, 18])
arr[::2,::2] # >>array([[ 0, 2, 4],
# [12, 14, 16],
# [24, 26, 28]])
arr[:,1] # >>array([ 1, 7, 13, 19, 25])
切片不会拷贝,直接使用的原视图,如果硬要拷贝,需要在后面加.copy()方法
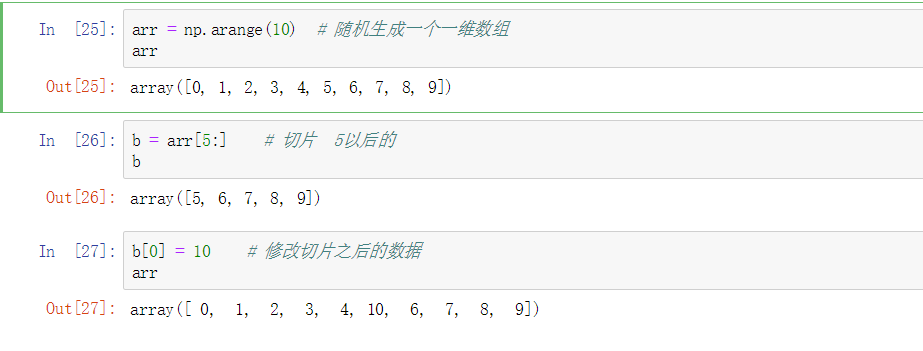
最后会发现修改切片后的数据影响的依然是原数据。有的人可能对一点机制有一些不理解的地方,像Python中内置的都有赋值的机制,而Numpy去没有,其实是因为NumPy的设计目的是处理大数据,所以你可以想象一下,假如NumPy坚持要将数据复制来复制去的话会产生何等的性能和内存问题。
- 布尔型索引
现在有这样一个需求:给一个数组,选出数组种所有大于5的数。
li = [random.randint(1,10) for _ in range(30)]
a = np.array(li)
a[a>5]
执行结果:
array([10, 7, 7, 9, 7, 9, 10, 9, 6, 8, 7, 6])
----------------------------------------------
原理:
a>5会对a中的每一个元素进行判断,返回一个布尔数组
a > 5的运行结果:
array([False, True, False, True, True, False, True, False, False,
False, False, False, False, False, False, True, False, True,
False, False, True, True, True, True, True, False, False,
False, False, True])
----------------------------------------------
布尔型索引:将同样大小的布尔数组传进索引,会返回一个有True对应位置的元素的数组
布尔型索引是numpy当中的一个非常常用的用法,通过布尔型索引取值方便又快捷。
4、通用函数
能对数组中所有元素同时进行运算的函数就是通用函数
4.1、常见通用函数
能够接受一个数组的叫做一元函数,接受两个数组的叫二元函数,结果返回的也是一个数组
- 一元函数:
| 函数 | 功能 |
|---|---|
| abs、fabs | 分别是计算整数和浮点数的绝对值 |
| sqrt | 计算各元素的平方根 |
| square | 计算各元素的平方 |
| exp | 计算各元素的指数e**x |
| log | 计算自然对数 |
| sign | 计算各元素的正负号 |
| ceil | 计算各元素的ceiling值 |
| floor | 计算各元素floor值,即小于等于该值的最大整数 |
| rint | 计算各元素的值四舍五入到最接近的整数,保留dtype |
| modf | 将数组的小数部分和整数部分以两个独立数组的形式返回,与Python的divmod方法类似 |
| isnan | 判断数组中的缺失值 |
| isinf | 表示那些元素是无穷的布尔型数组 |
| cos,sin,tan | 普通型和双曲型三角函数 |
以下简单演示常用的几个一元函数:
# 计算整数绝对值
arr = np.random.randint(-10,10,20)
np.abs(arr)
> array([9, 7, 3, 1, 5, 8, 7, 9, 4, 2, 7, 3, 4, 6, 6, 9, 2, 5, 8, 1])
-------------------------------------------------------------------------------
# 计算浮点数绝对值
arr = np.random.randn(2,5)
np.fabs(arr)
> array([[0.09892302, 0.06200835, 1.0324653 , 1.58089607, 0.44506652],
[0.34897694, 1.04843539, 0.83976969, 0.4731551 , 0.92229931]])
------------------------------------------------------------------------------
# 计算各元素的平方根
arr = np.arange(10)
np.sqrt(arr)
> array([0. , 1. , 1.41421356, 1.73205081, 2. ,
2.23606798, 2.44948974, 2.64575131, 2.82842712, 3. ])
- 二元函数:
| 函数 | 功能 |
|---|---|
| add | 将数组中对应的元素相加 |
| subtract | 从第一个数组中减去第二个数组中的元素 |
| multiply | 数组元素相乘 |
| divide、floor_divide | 除法或向下圆整除法(舍弃余数) |
| power | 对第一个数组中的元素A,根据第二个数组中的相应元素B计算A**B |
| maximum,fmax | 计算最大值,fmax忽略NAN |
| miximum,fmix | 计算最小值,fmin忽略NAN |
| mod | 元素的求模计算(除法的余数) |
arr = np.random.randint(0,10,5)
arr1 = np.random.randint(0,10,5)
arr,arr1
> (array([0, 1, 8, 2, 6]), array([5, 4, 1, 7, 0]))
-------------------------------------------------------------------------
# add 将数组中对应的元素相加
np.add(arr,arr1)
> array([5, 5, 9, 9, 6])
-------------------------------------------------------------------------
# subtract 从第一个数组中减去第二个数组中的元素
np.subtract(arr,arr1)
> array([-5, -3, 7, -5, 6])
-------------------------------------------------------------------------
# multiply 数组元素相乘
np.multiply(arr,arr1)
> array([ 0, 4, 8, 14, 0])
-------------------------------------------------------------------------
...
补充内容:浮点数特殊值
浮点数:float
浮点数有两个特殊值:
1、nan(Not a Number):不等于任何浮点数(nan != nan)
---------------------------------------------
2、inf(infinity):比任何浮点数都大
---------------------------------------------
- Numpy中创建特殊值:np.nan、np.inf
- 数据分析中,nan常被用作表示数据缺失值
以上函数使用非常方便,使用这些方法可以让数据分析的操作更加便捷。
4.2、数学统计方法
| 函数 | 功能 |
|---|---|
| sum | 求和 |
| cumsum | 求前缀和 |
| mean | 求平均数 |
| std | 求标准差 |
| var | 求方差 |
| min | 求最小值 |
| max | 求最大值 |
| argmin | 求最小值索引 |
| argmax | 求最大值索引 |
arr = np.random.randint(0,10,10)
arr
> array([2, 9, 6, 5, 4, 2, 9, 8, 0, 5])
-------------------------------------------------------------------------
# sum 求和
np.sum(arr)
> 50
-------------------------------------------------------------------------
# cumsum 求前缀和
np.cumsum(arr)
array([ 2, 11, 17, 22, 26, 28, 37, 45, 45, 50], dtype=int32) # 依次累加
-------------------------------------------------------------------------
# mean 求平均数
np.mean(arr)
> 5.0
-------------------------------------------------------------------------
# 由于此档内容太过简单,后续就不一一展示了
...
4.3、随机数
我们有学过python中生成随机数的模块random,在numpy中也有一个随机数生成函数,它在np.random的子包当中。在Python自带的random当中只能生成一些简单、基础的随机数,而在np.random当中是可以生成一些高级的随机数的。np.random要比Python自带的random包更加灵活。
| 函数 | 功能 |
|---|---|
| rand | 返回给定维度的随机数组(0到1之间的数) |
| randn | 返回给定维度的随机数组 |
| randint | 返回给定区间的随机整数 |
| choice | 给定的一维数组中随机选择 |
| shuffle | 原列表上将元素打乱(与random.shuffle相同) |
| uniform | 给定形状产生随机数组 |
| seed | 设定随机种子(使相同参数生成的随机数相同) |
| standard_normal | 生成正态分布的随机样本数 |
# rand 返回给定维度的随机数组
np.random.rand(2,2,2)
> array([[[0.37992696, 0.18115096],
[0.78854551, 0.05684808]],
[[0.69699724, 0.7786954 ],
[0.77740756, 0.25942256]]])
-------------------------------------------------------------------------
# randn 返回给定维度的随机数组
np.random.randn(2,4)
> array([[ 0.76676877, 0.21752554, 2.08444169, 1.51347609],
[-2.10082473, 1.00607292, -1.03711487, -1.80526763]])
-------------------------------------------------------------------------
# randint 返回给定区间的随机整数
np.random.randint(0,20)
> 15
-------------------------------------------------------------------------
# chocie 给定的一维数组中随机选择
np.random.choice(9,3) # # 从np.range(9)中,(默认)有放回地等概率选择三个数
> array([5, 8, 2])
np.random.choice(9,3,replace=False) # 无放回地选择
> array([1, 2, 0])
------------------------------------------------------------------------
# shuffle 原列表上将元素打乱(与random.shuffle相同)
arr = np.arange(10)
np.random.shuffle(arr)
arr
> array([4, 5, 0, 3, 7, 8, 9, 1, 2, 6])
------------------------------------------------------------------------
# uniform 给定形状产生随机数组
np.random.uniform(0,1,[3,3,3])
> array([[[0.80239474, 0.37170323, 0.5134832 ],
[0.42046889, 0.40245839, 0.0812019 ],
[0.8788738 , 0.48545176, 0.73723353]],
[[0.79057724, 0.80644632, 0.65966656],
[0.43833643, 0.53994887, 0.46762885],
[0.44472436, 0.08944074, 0.34148912]],
[[0.7042795 , 0.58397044, 0.13061102],
[0.22925123, 0.97745023, 0.14823085],
[0.6960559 , 0.07936633, 0.91221842]]])
------------------------------------------------------------------------
# seed 设定随机种子(使相同参数生成的随机数相同)
np.random.seed(0) # 当seed(0)时生成以下随机数组
np.random.rand(5)
> array([0.5488135 , 0.71518937, 0.60276338, 0.54488318, 0.4236548 ])
np.random.seed(2) # send(5)时生成以下随机数组
np.random.rand(5)
> array([0.5488135 , 0.71518937, 0.60276338, 0.54488318, 0.4236548 ])
np.random.seed(0) # 再次使用send(0)会发现返回最开始的随机数组
np.random.rand(5)
> array([0.5488135 , 0.71518937, 0.60276338, 0.54488318, 0.4236548 ])
------------------------------------------------------------------------
# standard_normal 生成正态分布的随机样本数
np.random.standard_normal([2,10])
> array([[-0.17937969, -0.69277058, 1.13782687, -0.16915725, -0.76391367,
-0.4980731 , -0.36289111, 0.26396031, -0.62964191, -0.4722584 ],
[-1.51336104, 1.10762468, 0.17623875, -0.94035354, 0.92959433,
-1.06279492, -0.88640627, 1.92134696, -0.45978052, -1.08903444]])
np.random和Python原生的random的区别:
| 比较内容 | random | np.random |
|---|---|---|
| 输入类型 | 非空的列表类型(包括列表、字符串和元组) | 非空的列表类型(包括列表、字符串和元组)+ numpy.array类型 |
| 输出维度 | 一个数或一个list(多个数) | 可指定复杂的size |
| 指定(a,b)范围 | 可以 | 整数可指定,浮点数不行,需自行转换 |
| 批量输出 | 不可 | 可。通过指定size参数 |
| 特定分布 | 涵盖了常用的几个分布; 只能单个输出 | 几乎涵盖了所有分布;可批量输出 |
只要能把以上所有的内容掌握,数据分析这门功夫你就算是打通了任督二脉了,学起来轻松又愉快。
5、数据表示
所有需要处理和构建模型所需的数据类型(电子表格、图像、音频等),其中很多都适合在 n 维数组中表示:
表格和电子表格
表格和电子表格是二维矩阵。电子表格中的每个工作表都可以是它自己的变量。python 中最流行的抽象是 pandas 数据帧,它实际上使用了 NumPy 并在其之上构建。
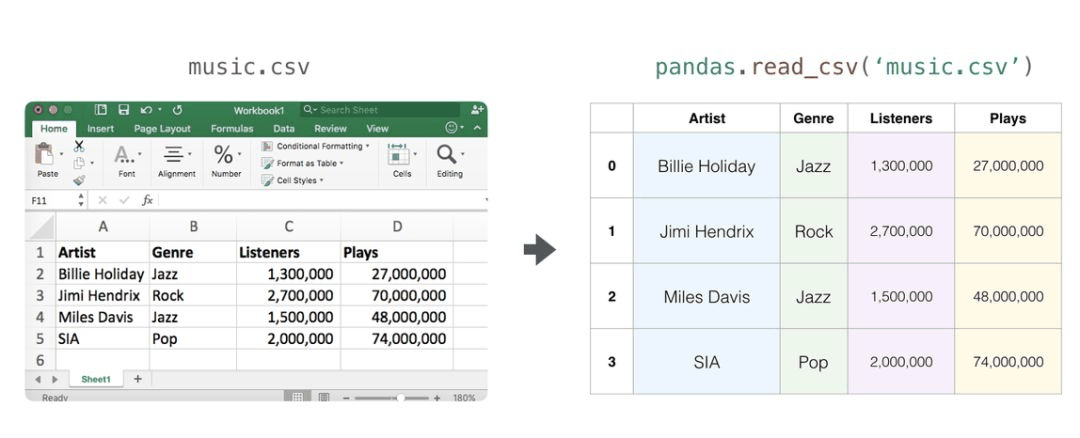
音频和时间序列
音频文件是样本的一维数组。每个样本都是一个数字,代表音频信号的一小部分。CD 质量的音频每秒包含 44,100 个样本,每个样本是-65535 到 65536 之间的整数。这意味着如果你有一个 10 秒的 CD 质量 WAVE 文件,你可以将它加载到长度为 10 * 44,100 = 441,000 的 NumPy 数组中。如果想要提取音频的第一秒,只需将文件加载到 audio 的 NumPy 数组中,然后获取 audio[:44100]。
以下是一段音频文件:
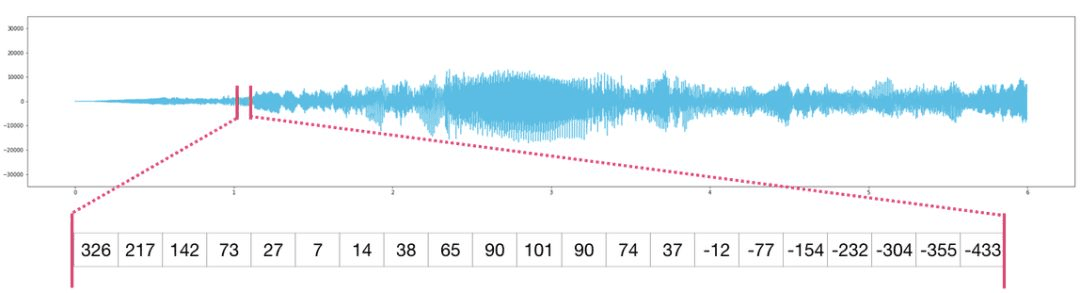
时间序列数据也是如此(如股票价格随时间变化)。
图像
图像是尺寸(高度 x 宽度)的像素矩阵。
如果图像是黑白(即灰度)的,则每个像素都可以用单个数字表示(通常在 0(黑色)和 255(白色)之间)。想要裁剪图像左上角 10 x 10 的像素吗?在 NumPy 写入即可。
下图是一个图像文件的片段:
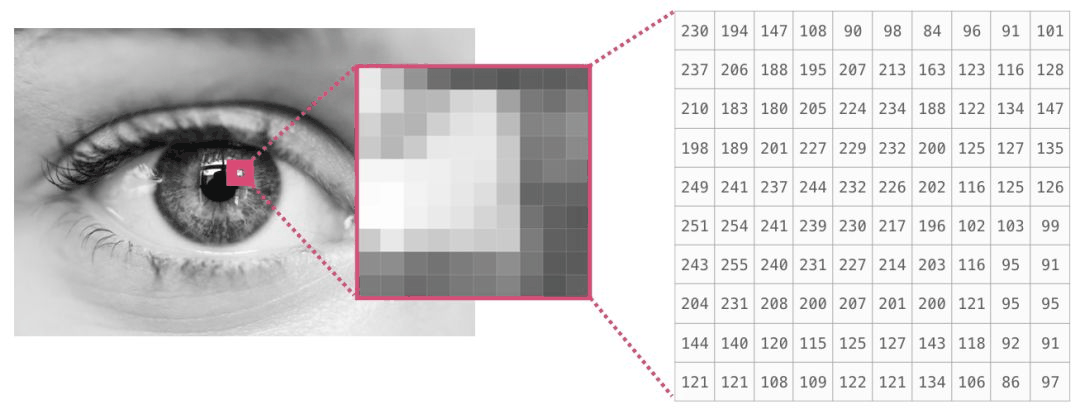
如果图像是彩色的,则每个像素由三个数字表示——红色、绿色和蓝色。在这种情况下,我们需要一个三维数组(因为每个单元格只能包含一个数字)。因此彩色图像由尺寸为(高 x 宽 x3)的 ndarray 表示:

6、总结
使用numpy,可以为我们提供一组丰富而又灵活的数据结构,以金融的角度来看的话下面几种类型是最重要的:
基本数据类型
在金融量化当中,整数、浮点数和字符串给我们提供了原子数据类型
标准数据结构
元组、列表、字典和集合,这些在金融当中有许多应用领域,列表通常是最为常用的
数组
说到数组肯定就是今天所学习的numpy中的ndarray数组,它对于数据的处理性能更高,代码更简洁、方便