【算法】动态规划

在开始学习动态规划的时候我总有这些问题：动态规划能解决什么问题？解决动态规划的思考过程是怎么样的？贪心、分治、回溯、动态规划这四种算法之间有什么区别和联系？

在解决这些问题之前，我要提一个理论：“一个模型三个特征”，即“多阶段决策最优解”模型，“最优子结构”、“无后效性”、“重复子问题”特征。

1.最优子结构

问题的解包含子问题的最优解。反过来说也就是，我们可以通过子问题的最优解，推导出问题的最优解。

2.无后效性

第一层含义是，在推到后面阶段的状态的时候，我们只关心前面阶段的状态值，不关心这个状态是怎么推导出来的；第二层含义是，某阶段的状态一旦确定，就不受之后阶段的决策影响。

3.重复子问题

不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。

这里用一个具体的动态规划问题来解释这个模型。

以 leetcode 64题为例：

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步
输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

一个模型

min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))

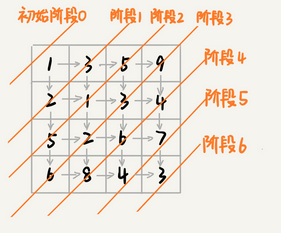
如图所示，每个阶段都有向右走或者向下走的俩种决策，每个阶段都会对应一个状态集合，我们把状态定义为min_dist(i,j)，其中i表示行，j表示列，min_dist(i,j)表示为走到matirx[i,j]时的最短距离，这就成了一个多阶段决策最优解问题，符合动态规划模型。

重复子问题：

如果将其使用回溯算法解决这个问题，在递归树中会出现重复节点，即到达这一步，会有多种路线，说明这个问题中存在重复子问题。

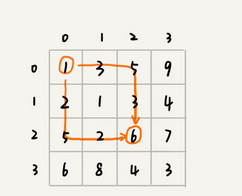
 无后效性：

走到(i,j)这个位置，只能通过(i-1,j),(i,j-1)这两个位置移动过来，也就是说，想要计算(i,j)位置对应的状态，只需要关心(i-1,j)，(i,j-1)俩个位置对应的状态，而且并不关心棋子是通过说明路线到达这俩个位置的。

最优子结构：

 min_dist(i,j) = w[i][j] + min(min_dist(i,j-1),min_dist(i-1,j))，也就是说，最短路径min_dist(i,j)肯定也包含到达这俩个位置(i,j-1)或(i-1,j)的最短路径之一。换句话说，min_dist(i,j)可以通过min_dist9i-1,j)或min_dist(i-1,j)两个状态推导出来。