【算法】大规模排序

归并排序和快速排序都比较适合大规模的数据排序。两者都用到了分治的思想。

---

归并排序

　　归并排序的核心思想蛮简单的，如果要排序一个数组，我们先把数组从中间分成前后俩部分，然后对前后俩部分分别排序，再将排好序的俩部分合并再一起。这样一步一步往下分而治之，将整个排序分成小的子问题来解决。

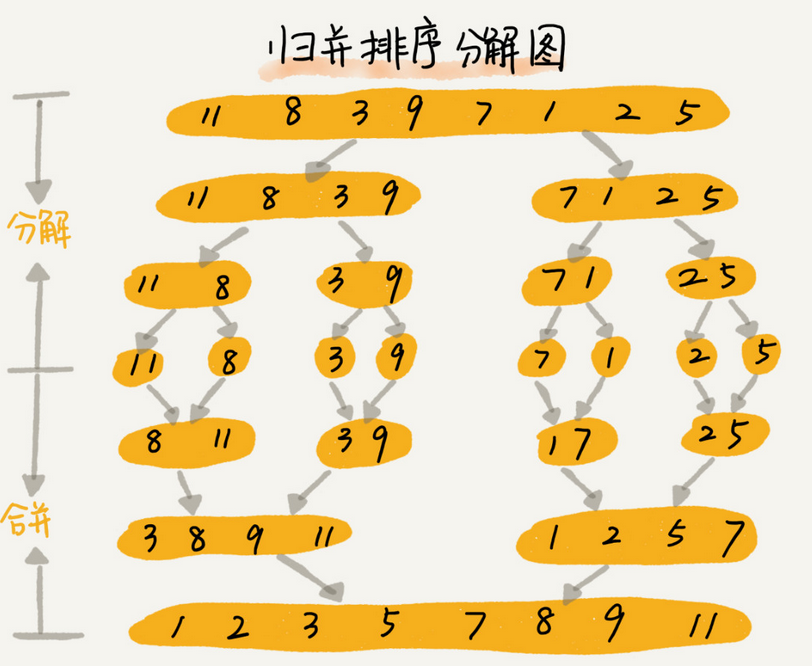
由于这个是个递归，所以 找出终止条件如下：

merge_sort(p...r) = merge(merge_sort(p...middle),merge_sort(middle+1...r)

其中当p >= r时不用再继续分解，或者如果是middle = middle // 2时，当middle == 1 不用再继续分解。

这个递归公式的解释如下：

merge_sort(p...r)表示，给下表从 p 到 r 之间的数组排序。我们将这个排序问题转化成了俩个子问题。 merge_sort(p..middle)和merge_sort (middle+1...r)

merge(left,right)的作用是将已经有序的 list[p...middle] 和 list[middle+1...r] 合并成一个数组。

def merge(left:list,right:list)->list:
    temp = list()
    if left[-1] <= right[0]:
        temp = left + right
        return temp
    if right[-1] <= left[0]:
        temp = right +left
        return temp
    left_index = right_index = 0
    while left_index <len(left) and right_index <len(right):
        if left[left_index] < right[right_index]:
            temp.append(left[left_index])
            left_index += 1
        else:
            temp.append(right[right_index])
            right_index += 1
    if left_index  == len(left):
        temp += right[right_index:]
    else:
        temp += left[left_index:]
    return temp
def merge_sort(li:list)->list:
    if len(li) <= 1:　　#因为是二分的关系，此时终止条件应该是为 1 ，不可能到 0 
        return li
    middle = len(li)//2
    left = merge_sort(li[:middle])
    right = merge_sort(li[middle:])
    return merge(left,right)

1.归并排序稳不稳定靠看 merge() 函数，也就是俩个有序子数组合并成一个有序数组的那部分代码。合并的过程中，如果 left[] 和 right[] 之间有值相同的函数，那么我们可以向代码那样，先把left[] 中的元素放入 temp数组。这样就可以保证值相同的元素，在合并前后的先后顺序不变，所以归并排序是一个稳定的排序算法。

2.归并排序的平均时间复杂度是 O(nlogn) 。其推导关系如下:

 T(1) = C #当n=1时，只要执行常量级的执行时间，表示为C
 T(n) = 2*T(n/2)  + n; n>1

#进一步分解：
T(n) = 2 * T(n/2) + n
     = 2 * (2 * T(n/4) + n/2) + n = 4 * T(n/4) + 2*n
     = 4 * (2 * T(n/8) + n/4) + 2 * n = 8 * T(n/8) + 3*n
     ......
     =2 ** k * T(n/(2 ** k)) + k * n

#当 T(n/(2 ** k)) = T(1)时， n/(2 ** k) = 1，即 k=(log2)n,回带入等式得： T(n) = Cn + n * (log2)n，即o(nlogn)

3.归并排序得时间复杂度在任何情况下都是 O(nlog2)，但是归并排序相对于快排而言没有应用广泛，因为归并排序并不是一个原地排序得算法。归并排序得合并函数，在合并俩个有序数组得时候，需要借助额外得存储空间。实际上，递归函数得空间复杂度并不能像时间复杂度那样累加，尽管每次合并操作都要申请额外得内存空间，但是在合并完成以后，临时开辟得空间也就会被释放掉了。所以在任意时刻，CPU只会有一个函数在执行，也就只有一个临时得内存空间在使用。临时内存空间最大也不会超过 n 个数据得大小，所以空间复杂度为 O(n)。

---

快速排序