一、算法思想
归并排序,是创建在归并操作上的一种有效的排序算法。算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。
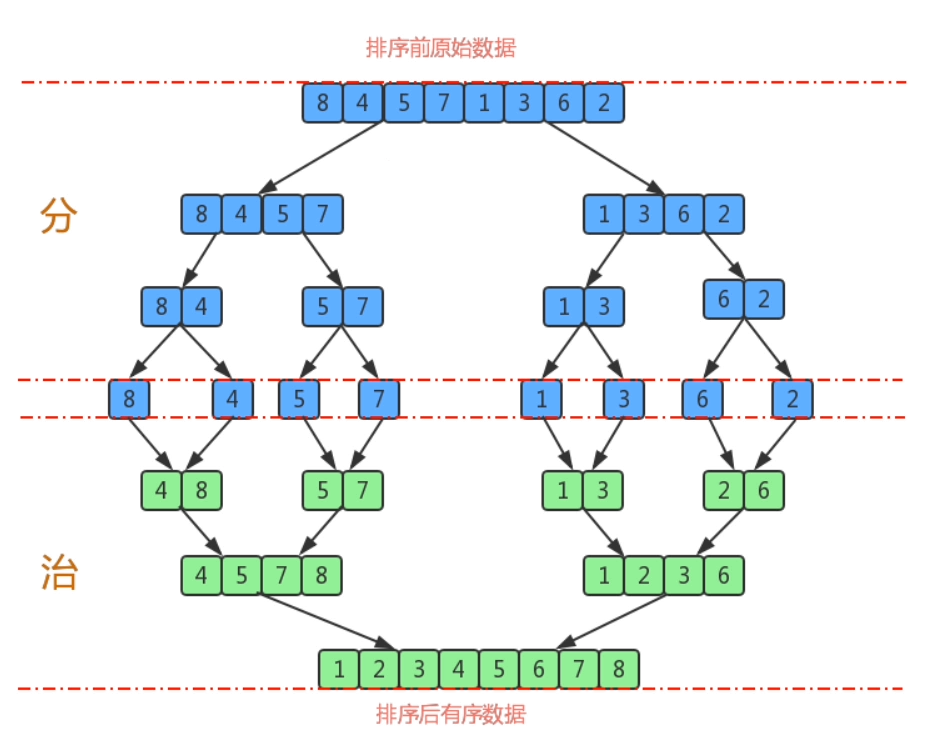
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
分解(Divide):将n个元素分成个含n/2个元素的子序列。
解决(Conquer):用合并排序法对两个子序列递归的排序。
合并(Combine):合并两个已排序的子序列已得到排序结果。
二、算法流程
迭代法
① 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
② 设定两个指针,最初位置分别为两个已经排序序列的起始位置
③ 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
④ 重复步骤③直到某一指针到达序列尾
⑤ 将另一序列剩下的所有元素直接复制到合并序列尾
递归法
① 将序列每相邻两个数字进行归并操作,形成floor(n/2)个序列,排序后每个序列包含两个元素
② 将上述序列再次归并,形成floor(n/4)个序列,每个序列包含四个元素
③ 重复步骤②,直到所有元素排序完毕
三、算法实现
1 //归并排序 2 static class MergeSort implements Sort { 3 private static Comparable[] assist; 4 @Override 5 public String sortName() { 6 return "归并排序"; 7 } 8 @Override 9 public Comparable[] sort(Comparable[] data) { 10 assist = new Comparable[data.length]; 11 int lo = 0; 12 int hi = data.length - 1; 13 sort(data, lo, hi); 14 return data; 15 } 16 //递归体 17 private static void sort(Comparable[] data, int lo, int hi) { 18 if(hi <= lo) return; 19 int mid = lo + (hi - lo) / 2; 20 sort(data, lo, mid); 21 sort(data, mid + 1, hi); 22 merge(data, lo, mid, hi); 23 } 24 //合并 25 private static void merge(Comparable[] data, int lo, int mid, int hi) { 26 //定义三个指针 27 int i = lo, p1 = lo, p2 = mid + 1; 28 //遍历,移动p1指针和p2指针,比较对应索引处的值,找出小的那个,放到辅助数组的对应索引处 29 while(p1 <= mid && p2 <= hi) { 30 if(!Sort.greater(data[p1], data[p2])) { 31 assist[i++] = data[p1++]; 32 } else { 33 assist[i++] = data[p2++]; 34 } 35 } 36 //遍历,如果p1指针没有走完,那么顺序移动p1指针,把对应的元素放到辅助数组的对应索引处 37 while(p1 <= mid) { 38 assist[i++] = data[p1++]; 39 } 40 //遍历,如果p2指针没有走完,那么顺序移动p1指针,把对应的元素放到辅助数组的对应索引处 41 while(p2 <= hi) { 42 assist[i++] = data[p2++]; 43 } 44 //把辅助数组中的元素拷贝到原数组中 45 for(int index = lo; index <= hi; index++) { 46 data[index] = assist[index]; 47 } 48 } 49 }
四、算法分析
复杂度
这个关系式的含义是,对长度为 的数组进行排序的时间复杂度等于对两个长度为
的数组排序的时间复杂度,再加上分割和归并的时间复杂度
。根据前面的公式,我们可以得到归并排序的时间复杂度为
。由于归并过程需要长度为
的空数组,所以归并排序的空间复杂度为
。
稳定性
归并排序算法中,归并最后到底都是相邻元素之间的比较交换,并不会发生相同元素的相对位置发生变化,故是稳定性算法。