线性表的删除

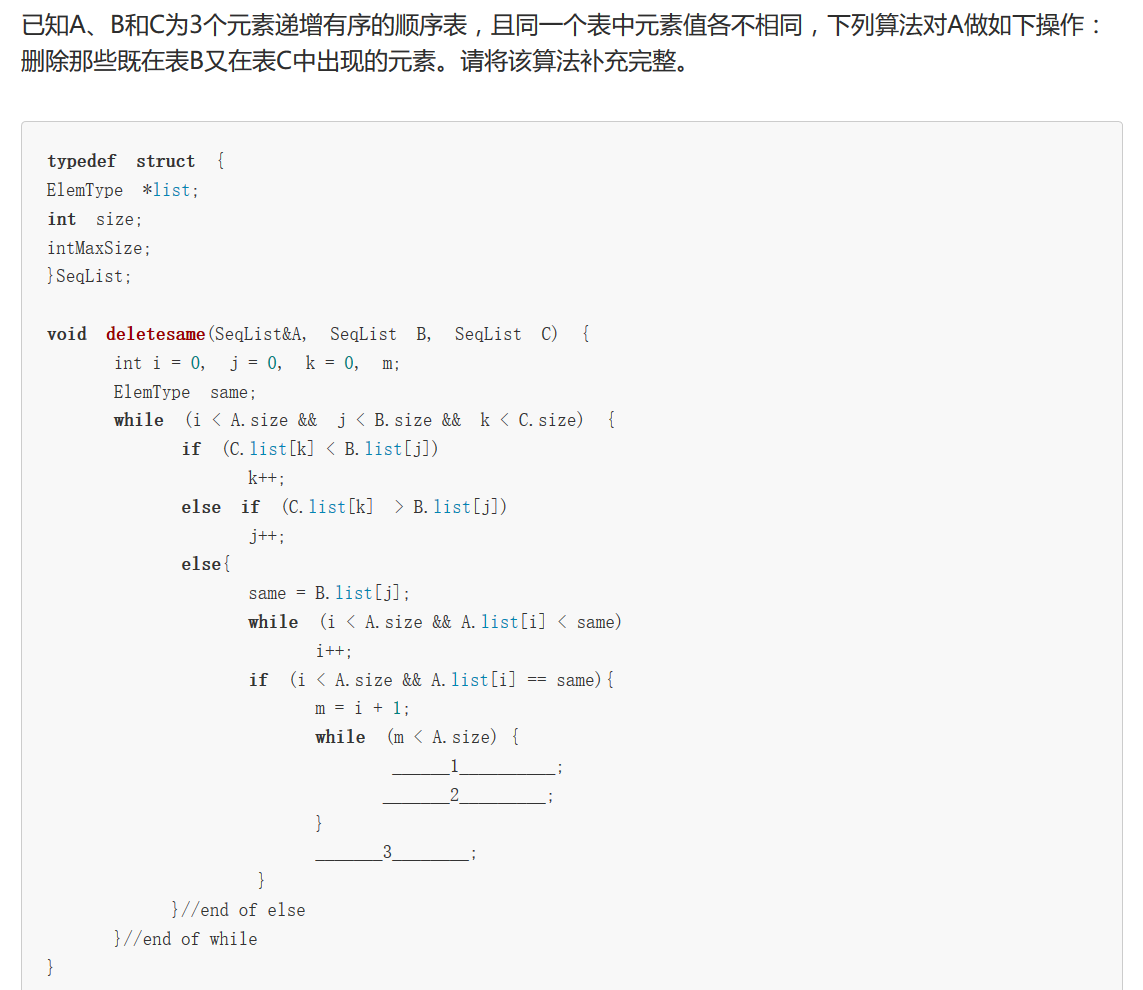
　　学习了线性表之后发现删除的方式有多种多样，同时出题的方式也千奇百怪。

首先是最简单的删除：把要删除元素之后的元素全部往前挪，将欲删除的覆盖掉。

但是这种删除方式的局限性太大了，首先就是时间复杂度，这个算法的时间复杂度为O（n^2）.

bool Delete( List L, Position P )
{
    int i;
    if(P>=L->Last||P<0)
    {
        printf("POSITION %d EMPTY",P);
        return false;
    }
        L->Last--;//这里的Last是指长度了
    for(i=P;i<L->Last;i++)
        L->Data[i]=L->Data[i+1];
    return true;
}

　　这个算法遇到对时间有要求的情况基本就崩了。

例：

6-2 线性表元素的区间删除（20 分）

给定一个顺序存储的线性表，请设计一个函数删除所有值大于min而且小于max的元素。删除后表中剩余元素保持顺序存储，并且相对位置不能改变。

函数接口定义：

List Delete( List L, ElementType minD, ElementType maxD );

其中List结构定义如下：

typedef int Position;
typedef struct LNode *List;
struct LNode {
    ElementType Data[MAXSIZE];
    Position Last; /* 保存线性表中最后一个元素的位置 */
};

L是用户传入的一个线性表，其中ElementType元素可以通过>、==、<进行比较；minD和maxD分别为待删除元素的值域的下、上界。函数Delete应将Data[]中所有值大于minD而且小于maxD的元素删除，同时保证表中剩余元素保持顺序存储，并且相对位置不变，最后返回删除后的表。

裁判测试程序样例：

#include <stdio.h>

#define MAXSIZE 20
typedef int ElementType;

typedef int Position;
typedef struct LNode *List;
struct LNode {
    ElementType Data[MAXSIZE];
    Position Last; /* 保存线性表中最后一个元素的位置 */
};

List ReadInput(); /* 裁判实现，细节不表。元素从下标0开始存储 */
void PrintList( List L ); /* 裁判实现，细节不表 */
List Delete( List L, ElementType minD, ElementType maxD );

int main()
{
    List L;
    ElementType minD, maxD;
    int i;

    L = ReadInput();
    scanf("%d %d", &minD, &maxD);
    L = Delete( L, minD, maxD );
    PrintList( L );

    return 0;
}

/* 你的代码将被嵌在这里 */

输入样例：

10
4 -8 2 12 1 5 9 3 3 10
0 4

输出样例：

4 -8 12 5 9 10

由于这题有些函数需要裁判完成，我写了一个能测试的main函数

复制过去就能在编译器上测试了。

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 20
typedef int ElementType;

typedef int Position;
typedef struct LNode *List;
struct LNode {
    ElementType Data[MAXSIZE];
    Position Last; /* 保存线性表中最后一个元素的位置 */
};
List Insert( List L, ElementType X, Position P );
List ReadInput(); /* 裁判实现，细节不表。元素从下标0开始存储 */
void PrintList( List L ); /* 裁判实现，细节不表 */
List Delete( List L, ElementType minD, ElementType maxD );
List MakeEmpty();
int main()
{
    List L;
    ElementType minD, maxD,N,X=0,P;
    int i;

    scanf("%d", &N);
    L=MakeEmpty();
    while ( N-- ) {
        scanf("%d",&P);
        L=Insert(L, X, P);
            X++;
    }
    L->Last--; 
   // for(i=0;i<L->Last;i++)
    //    printf("%d ",L->Data[i]);
    scanf("%d %d", &minD, &maxD);
    L = Delete( L, minD, maxD );
    for(i=0;i<=L->Last;i++)
        printf("%d ",L->Data[i]);

    return 0;
}
List MakeEmpty()
{
    List ptr;
    ptr=(List)malloc(sizeof(struct LNode));
    ptr->Last=0;
    return ptr;
}
List Insert( List L, ElementType X, Position P )
{
    if(!L)return false;
    int i=0;


    L->Data[X]=P;
    L->Last++;
    return L;
}
/*你的代码插在这*/

这里有一个很重要的点这里的L->Last是下标！！！

此题有多种解法，我先列出三种

1.会超时的，也就是刚才的删除法

List Delete( List L, ElementType minD, ElementType maxD )
{
    int i=0,j;
    if(!L)return L;
    if(minD>=maxD)return L;
    while(i<=L->Last)
    {
        if(L->Data[i]<maxD&&L->Data[i]>minD)
        {
            L->Last--;
            for(j=i;j<=L->Last;j++)
            {
                L->Data[j]=L->Data[j+1];
            }
        }
        else
        i++;
    }
    return L;
}

2.第二种算法的思路就是，建立一个辅助数组，将不想删除的数记录下来，遍历完一次数组过后，在将数组的内容抄录到线性表中，

同时L->Last的大小也变为不想删除的数的个数。

虽然这算法使时间复杂度变为O（n）了，但是这种算法的局限性是多定义了一个数组，导致空间复杂度变大。

List Delete( List L, ElementType minD, ElementType maxD )
{
    int i=0,count=0;
    if(!L)return L;
    if(minD>=maxD)return L;
    int a[L->Last+1];//辅助数组
    while(i<=L->Last)
    {
        if(L->Data[i]<=minD||L->Data[i]>=maxD)
        {
            a[count]=L->Data[i];
            count++;//记录个数
        }
        i++;
    }
    L->Last=--count;//L->Last是下标，所以，减少一个
    for(i=0;i<=count;i++)
        L->Data[i]=a[i];
    return L;
} 

3.这是问其他人后得知的（感谢感谢他）

思路是：

遍历一遍数组，遇到要删除的元素把数量记录下来，遇到不删除的元素前移，覆盖掉要删除的元素。结束后整个长度剪掉删除数就好了。

假定我需要删除1  4中的元素（不包括1和4哦）

 

代码：

List Delete( List L, ElementType minD, ElementType maxD )
{
    int i=0,count=0;
    if(!L)return L;
    if(minD>=maxD)return L;
    for(;i<=L->Last;i++)
    {
        if(L->Data[i]>minD&&L->Data[i]<maxD)
            count++;//计算数量
        else
            L->Data[i-count]=L->Data[i];//往前挪动
    }
    L->Last-=count;//长度变短
    return L;
}

还有两题课后练习题，也挺有意思的。