问题描述
二分查找时间复杂度为O(log2n).
二分查找效率相对来说比较高.但是传入的数组必须是已经排好序的数组.
有两种思路:
第一种是动态改变下标.进行与所要查找数组进行对比.得出结果
第二种是使用递归.动态改变数组分解为子数组求解.进而得出结果
- 这个对于递归这个方法来说是比较简单的.
- 只是把原问题分解为若干子问题.
- 将子问题求解.
- 而没有涉及到将子问题的结果合并为原问题.(这是递归中最难的一个步骤)
- 只是把原问题分解为若干子问题.
下面的一张图可能帮助到你更好的理解二分查找.原图来自动画参考链接-小鹿动画学编程
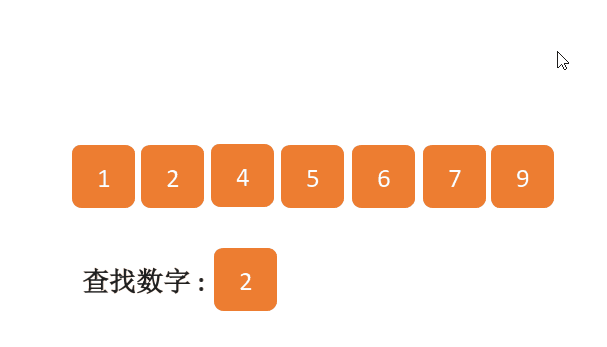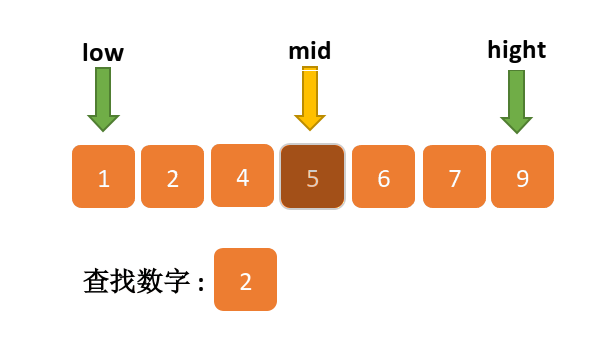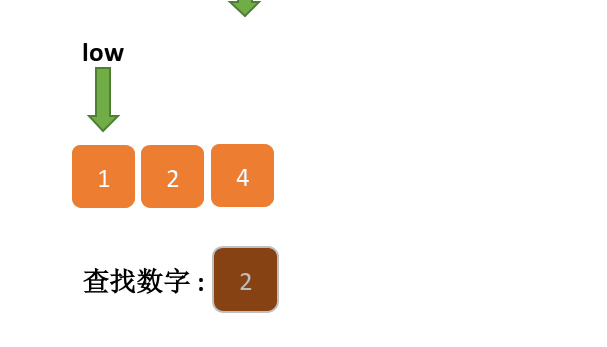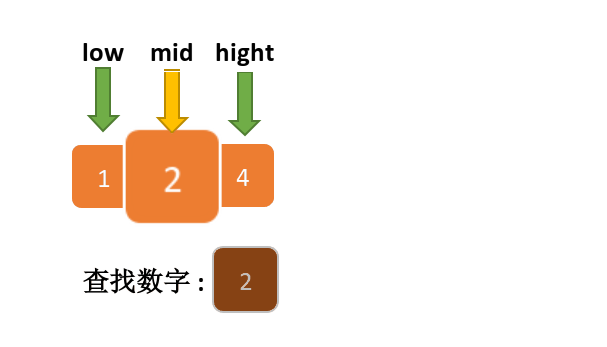
方法一:动态改变下标
def binary_search(sort_list,search_value):
start_index = 0
end_index = len(sort_list)-1
count = 0
result = False
while start_index <= end_index:
middle = (start_index + end_index) // 2
count = count +1
if sort_list[middle] == search_value:
result= not result # 返回其所查找下标与查找次数
elif sort_list[middle] < search_value: # 要查找的值大于中间值,在右边.
start_index = middle + 1
else:
end_index = middle - 1
return result
方法二:使用递归
Python中数组切片的操作是O(k)的,以下代码采用切片是为了易于阅读.更加高效的方式是使用数组下标.2020/03/17
def binary_search_recursion(sorted_list,search_value,count): # 递归版本
list_len = len(sorted_list)
count = count +1
if list_len == 0:
return False
middle = list_len // 2
if sorted_list[middle] == search_value:
return count # 可改为True
elif search_value > sorted_list[middle]: # 查找值大于中间值.也就是查找值在数组右边
return binary_search_recursion(sorted_list[middle+1:],search_value,count)
else: # 查找值小于中间值.也就是查找值在数组左边
return binary_search_recursion(sorted_list[:middle-1],search_value,count)
testlist=[0, 1, 2, 8, 13, 17, 19, 32, 42]
print(binary_search_recursion(testlist,17,0)) # 查找二次