问题描述
找出数组中存在的最大子数组(必须相连).(数组有正数与负数).
示例: arr = [-1,-3,3,5,-4,3,2,-2,3,6].
还原为实际场景可能是在一些具有相同属性的存在中,找出一段连续且最佳的存在.
方法一:暴力破解法
思路解释:使用暴力破解法.
时间复杂度为O(n^2).
# 使用暴力破解法.
def max_violent(arr):
max_value = arr[0]
index_for_left =0
index_for_right =0
for i in range(len(arr)):
for j in range(i,len(arr)):
temporary_value = 0 # 基于Python的特性,可以将这行代码以及第三层for替换为:temporary_value = sum(arr[i:j])
for k in range(i,j+1):
temporary_value = temporary_value + arr[k]
if(temporary_value>max_value):
max_value = temporary_value
index_for_left = i
index_for_right = j
return (max_value,index_for_left,index_for_right)
arr = [-1,-3,3,5,-4,3,2,-2,3,6]
print(max_violent(arr))
方法二:二分法
def violence(l = []):
maxVal = 0
x,y=0,0
for i in range(0,len(l)+1):
for j in range(0,len(l)+1):
res = sum(l[i:j])
if res > maxVal:
maxVal = res
x = i
y = j
return maxVal,x,y
#分治法 想左扫 向右扫,求出两边的最大值
def left_or_right(l):
maxVal = 0
term = 0
for i in l:
term += i
if maxVal < term:
maxVal = term
return maxVal
def Separate(l):
middle = int(len(l)/2)
l1 = l[0:middle]
l2 = l[middle:len(l)]
#左半部分
maxVal1,x1,y1 = violence(l1)
#右半部分
maxVal2,x2,y2 = violence(l2)
#跨立在中间
max_right = left_or_right(l2)
max_left = left_or_right(l1[::-1]) # 倒着扫描
#print('---')
#print(max_right)
#print(l1[::-1])
#print('---')
maxVal3 = max_right + max_left
return (maxVal1,maxVal2,maxVal3)
arr = [-1,-3,3,5,-4,3,2,-2,3,6]
val = Separate(arr)
print(val)
print(max(val))
方法三:使用递归
使用递归将时间复杂度降低到O(lgn).
将一个主问题分解为若干子问题,进而将各个子问题的解.
也就是递归的思想 -> 分而治之:
- 原问题分解成多个子问题
- 递归的求解各个子问题
- 将结果合并为原问题解
def max_digui(arr,low,high): # 使用递归
if low==high: # 递归结束条件
return arr[low]
mid=(low+high)//2 # 向下取整
m1=max_digui(arr,low,mid) # 递归
m2=max_digui(arr,mid+1,high) # 递归
now_left=arr[mid]
maxleft=now_left
for i in range(mid-1,low-1,-1): # 倒序循环
now_left=now_left+arr[i]
if now_left>maxleft:
maxleft=now_left
now_right=arr[mid+1]
maxright=now_right
for j in range(mid+2,high+1):
now_right=now_right+arr[j]
if now_right>maxright:
maxright=now_right
m3=maxleft+maxright
return max(m1,m2,m3)
arr = [-1,-3,3,5,-4,3,2,-2,3,6]
print(max_digui(arr,0,len(arr)-1)) # 16找出的是最大值
方法四:使用动态规划
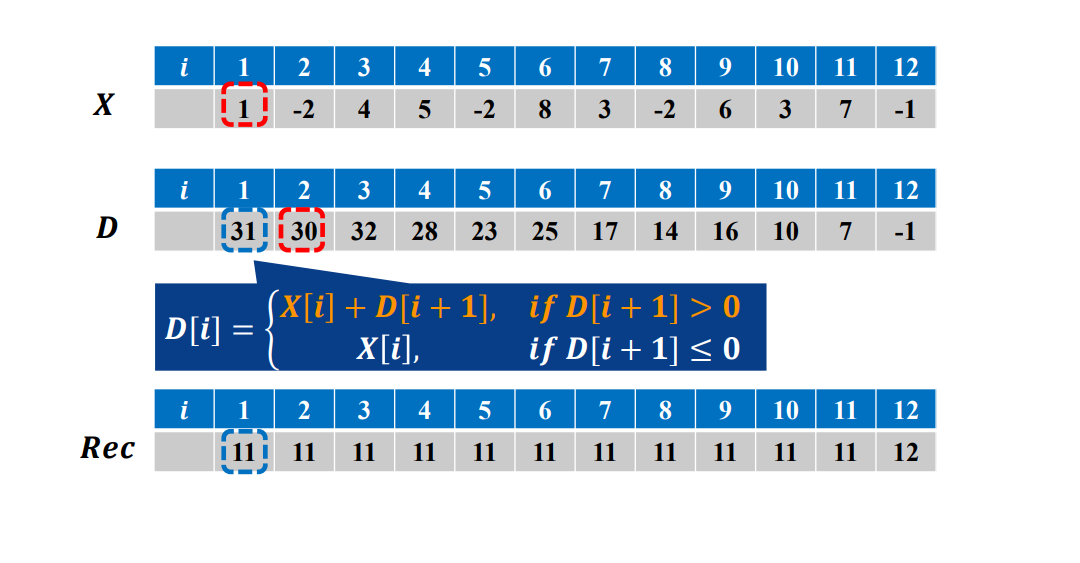
- 从数组最后的元素开始计算.
- list[i]表示当前元素.d[i+1]表示d[i+1]的最优子数组的值.
- 默认当前元素的最大子数组(list[i])是其本身.
- 如果d[i+1] > 0.那么就加入后面的元素列表.
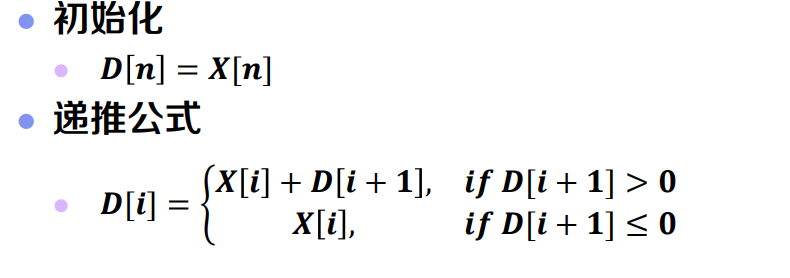
-
使用最优规划的逻辑
- 是确保每一个子问题都是最优解
- 自底向上的运算
- 一直解到所求的答案为止
-
变量说明
- alist是数据数组
- list_dp 是记录当前元素最优值的表.
- list_rec 是记录当前元素最优值终止的下标.
def max_liat_dp(alist,list_dp,list_rec):
max_num_now = alist[len(alist)-1]# 最后一个元素的的最大值默认是其本身.
list_dp[len(alist)-1] = max_num_now # 记录进表中
list_rec[len(alist)-1] = len(alist) - 1 # 最后一个元素的比较结束下标默认是本身
for i in range(len(alist)-2,-1,-1): # 从倒数第二个元素到第0个元素.
max_num_now = alist[i]
list_rec[i] = i
if list_dp[i+1] > 0: # 如果上一个元素的最优值大于0,那么就执行加入操作.
max_num_now = max_num_now + list_dp[i+1]
list_rec[i] = list_rec[i+1]
list_dp[i] = max_num_now
return (list_dp,list_rec)
# 算法结束.
# ------------------
# 以下是数据测试类,用于测试算法正确性,非排序算法本身函数.
# 可以删除TestDate类,手动填入数据测试.
'''
import unittest
import random
class TestData(unittest.TestCase):
def create_data(self,num_start,num_end,num_length): # 生成list
return [random.randint(num_start,num_end) for i in range(num_length)]
def test_case1(self):
'''
# alist是数据数组
# list_dp 是记录最优值的表.
# list_rec 是记录终止位置.
'''
alist = [1,-2,4,5,-2,8,3,-2,6,3,7,-1]
list_dp = [0]*len(alist)
list_rec = [0]*len(alist)
print(max_liat_dp(alist,list_dp,list_rec))
print(max(list_dp))
print('
'*1)
def test_case2(self):
alist = self.create_data(-50,50,8)
list_dp = [0]*len(alist)
list_rec = [0]*len(alist)
print(max_liat_dp(alist,list_dp,list_rec))
print(max(list_dp))
print('
'*1)
def test_case3(self):
alist = self.create_data(-10,50,8)
list_dp = [0]*len(alist)
list_rec = [0]*len(alist)
print(max_liat_dp(alist,list_dp,list_rec))
print(max(list_dp))
print('
'*1)
def test_case4(self):
alist = self.create_data(1,50,5)
list_dp = [0]*len(alist)
list_rec = [0]*len(alist)
print(max_liat_dp(alist,list_dp,list_rec))
print(max(list_dp))
print('
'*1)
if __name__ == "__main__":
unittest.main() # 调用测试数据
# alist是数据数组
# list_dp 是记录最优值的表.
# list_rec 是记录终止位置.