二分查找的实际应用

一、什么是二分查找？

　　二分查找针对的是一个有序的数据集合，每次通过跟区间中间的元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间缩小为0。

二、惊人的查找速度 O(logn)

　　我们假设数据大小是 n，每次查找后数据都会缩小为原来的一半，也就是会除以 2。最坏情况下，直到查找区间被缩小为空，才停止。

　　可以看出来，这是一个等比数列。其中 n/2^k=1 时，k 的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较，所以，经过了 k 次区间缩小操作，时间复杂度就是 O(k)。通过 n/2^k=1，我们可以求得 ，所以时间复杂度就是 O(logn)。

　　除了二分查找，后面还会遇到的 堆、二叉树的操作，它们时间复杂度也是 O(logn)。这里就再深入地讲讲 O(logn) 这种对数时间复杂度。这是一种极其高效的时间复杂度，有的时候甚至比时间复杂度是常量级O(1) 的算法还要高效。为什么这么说呢？

　　因为 logn 是一个非常“恐怖”的数量级，即便 n 非常非常大，对应的 logn 也很小。比如 n 等于 2 的 32 次方，这个数很大了吧？大约是 42 亿。也就是说，如果我们在 42 亿个数据中用二分查找一个数据，最多需要比较 32 次。

　　我们前面讲过，用大 O 标记法表示时间复杂度的时候，会省略掉常数、系数和低阶。对于常量级时间复杂度的算法来说，O(1) 有可能表示的是一个非常大的常量值，比如 O(1000)、O(10000)。所以，常量级时间复杂度的算法有时候可能还没有O(logn) 的算法执行效率高。

　　反过来，对数对应的就是指数。有一个非常著名的“阿基米德与国王下棋的故事”，你可以自行搜索一下，感受一下指数的”恐怖”。这也是为什么我们说，指数级时间复杂度的算法在大规模数据面前是无效的。

三、二分查找的递归与非递归实现

　　最简单的情况就是有序数组中不存在重复元素，使用二分查找值等于给定值的数据。代码如下：

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid = (low + high) / 2;
    if (a[mid] == value) {
      return mid;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      high = mid - 1;
    }
  }
  return -1;
}

着重强调一下容易出错的 3 个地方。

1. 循环退出条件：注意是 low<=high，而不是 low<high

2. mid 的取值：mid=(low+high)/2 这种写法是有问题的。因为如果 low 和 high 比较大的话，两者之和就有可能会溢出。改进的方法是将 mid 的计算方式写成 low+(high-low)/2。更进一步，如果要将性能优化到极致的话，我们可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)。因为相比除法运算来说，计算机处理位运算要快得多。

3. low 和 high 的更新：low=mid+1，high=mid-1。注意这里的 +1 和 -1，如果直接写成 low=mid 或者 high=mid，就可能会发生死循环。比如，当 high=3，low=3 时，如果 a[3] 不等于value，就会导致一直循环不退出。

结合以上三点用递归实现，代码如下：

// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {
  return bsearchInternally(a, 0, n - 1, val);
}
private int bsearchInternally(int[] a, int low, int high, int value) {
  if (low > high) return -1;
  int mid =  low + ((high - low) >> 1);
  if (a[mid] == value) {
    return mid;
  } else if (a[mid] < value) {
    return bsearchInternally(a, mid+1, high, value);
  } else {
    return bsearchInternally(a, low, mid-1, value);
  }
}

　　

四、二分查找应用场景的局限性

　　二分查找的时间复杂度是 O(logn)，查找数据的效率非常高。不过，并不是什么情况下都可以用二分查找，它的应用场景是有很大局限性的。那什么情况下适合用二分查找，什么情况下不适合呢？

• 首先，二分查找依赖的是顺序表结构，简单点说就是数组。

　　二分查找只能用在数据是通过顺序表来存储的数据结构上。如果你的数据是通过其他数据结构存储的，则无法应用二分查找。

• 其次，二分查找针对的是有序数据。

　　二分查找对这一点的要求比较苛刻，数据必须是有序的。如果数据没有序，我们需要先排序。前面章节里我们讲到，排序的时间复杂度最低是 O(nlogn)。所以，如果我们针对的是一组静态的数据，没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低。

　　但是，如果我们的数据集合有频繁的插入和删除操作，要想用二分查找，要么每次插入、删除操作之后保证数据仍然有序，要么在每次二分查找之前都先进行排序。针对这种动态数据集合，无论哪种方法，维护有序的成本都是很高的。

　　所以，二分查找只能用在插入、删除操作不频繁，一次排序多次查找的场景中。针对动态变化的数据集合，二分查找将不再适用。那针对动态数据集合，如何在其中快速查找某个数据呢？二叉树那节会讲到。

• 再次，数据量太小不适合二分查找。

　　数据量很小时，顺序遍历就足够了，完全没有必要用二分查找。只有数据量比较大的时候，二分查找的优势才会比较明显。

　　有一个例外。如果数据之间的比较操作非常耗时，不管数据量大小，都推荐使用二分查找。比如，数组中存储的都是长度超过 300 的字符串，如此长的两个字符串之间比对大小，就会非常耗时。我们需要尽可能地减少比较次数，而比较次数的减少会大大提高性能，这个时候二分查找就比顺序遍历更有优势。

• 最后，数据量太大也不适合二分查找。

　　二分查找的底层需要依赖数组这种数据结构，而数组为了支持随机访问的特性，要求内存空间连续，对内存的要求比较苛刻。比如，我们有 1GB 大小的数据，如果希望用数组来存储，那就需要 1GB 的连续内存空间。

　　注意这里的“连续”二字，也就是说，即便有 2GB 的内存空间剩余，但是如果这剩余的 2GB 内存空间都是零散的，没有连续的 1GB 大小的内存空间，那照样无法申请一个 1GB 大小的内存空间，那照样无法申请一个 1GB 大小的数组。而我们的二分查找是作用在数组这种数据结构之上的，所以太大的数据用数组存储就比较吃力了，也就不能用二分查找了。

五、如何在 1000 万个整数中快速查找某个整数？

　　我们的内存限制是 100MB，每个数据大小是 8 字节，最简单的办法就是将数据存储在数组中，内存占用差不多是 80MB，符合内存的限制。我们可以先对这 1000 万数据从小到大排序，然后再利用二分查找算法，就可以快速地查找想要的数据了。

六、二分查找之变形问题

1、查找第一个值等于给定值的元素

　　　　比如下面这样一个有序数组，其中，a[5]，a[6]，a[7]的值都等于 8，是重复的数据。我们希望查找第一个等于 8 的数据，也就是下标是 5 的元素。

　　　　

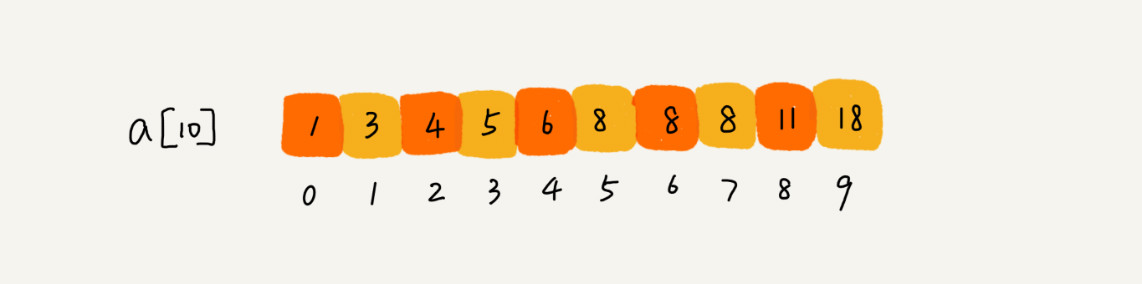
　　极致简洁的写法：

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid = low + ((high - low) >> 1);
    if (a[mid] >= value) {
      high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  if (low < n && a[low]==value){ return low;}
  else {return -1;}
}

　　易懂的写法：

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == 0) || (a[mid - 1] != value)){ return mid;}
      else {high = mid - 1;}
    }
  }
  return -1;
}

2、查找最后一个值等于给定值的元素

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] != value)) {return mid;}
      else {low = mid + 1;}
    }
  }
  return -1;
}

3、查找第一个大于等于给定值的元素

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] >= value) {
      if ((mid == 0) || (a[mid - 1] < value)) {return mid;}
      else {high = mid - 1;}
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

4、查找最后一个小于等于给定值的元素

public int bsearch7(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] > value)) {return mid;}
      else {low = mid + 1;}
    }
  }
  return -1;
}

　　

七、不用库函数求一个数的平方根

 　（1）采用 牛顿迭代法。

    （2）牛顿迭代法简介

               假设方程 在  附近有一个根，那么用以下迭代式子：
                                         
       依次计算、、、……，那么序列将无限逼近方程的根。

                牛顿迭代法的原理很简单，其实是根据f(x)在x0附近的值和斜率，估计f(x)和x轴的交点，看下面的动态图：

                                 

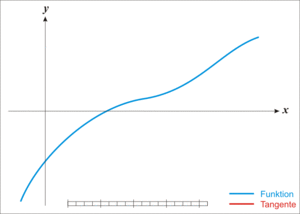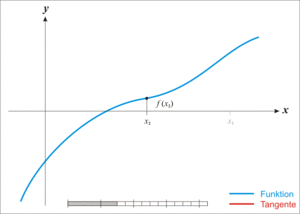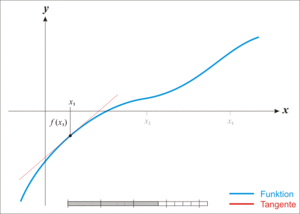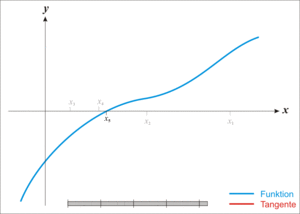
     （3）用牛顿迭代法开平方

                   令：                        
                  所以f(x)的一次导是 ： 
                  牛顿迭代式：
                                              

                  随便一个迭代的初始值，例如，代入上面的式子迭代。

                  例如计算，即a=2：
                                
                                
                               

     （4）代码

public class Sqr {
    public static void main(String[] args) {
        // TODO 自动生成的方法存根
        Scanner scan = new Scanner(System.in);

        DecimalFormat df = new DecimalFormat("#.000");
        int sc = scan.nextInt();
        System.out.print(sc + "的算术平方根是：");
        System.out.println(df.format(SQR(sc)));
    }
    public static double SQR(int a) {
        double x1 = 1, x2;
        x2 = x1 / 2.0 + a / (2 * x1);//牛顿迭代公式
        while (Math.abs(x2 - x1) > 1e-4) {
            x1 = x2;
            x2 = x1 / 2.0 + a / (2 * x1);
        }
        return x2;
    }
}

　　

　　二分法解答，代码如下：

public class SqrtUtil {
    /**
     * 方法1 精确度差
     * @param data
     * @return
     */
    public static double getSquareRoot(int data){
        if(data < 0){
            return -1;
        }
        double low = 0.0;
        double high = data;
        double mid = 0.0;
        while(isNumOfDigLessThenInput(mid, 6) ){
            mid = low + ((high - low) / 2);
            if(data == mid*mid){
                return mid;
            }else if(data < mid*mid){
                high = mid;
            }else{
                low = mid;
            }
        }
        return mid;
    }

    private static boolean isNumOfDigLessThenInput(double data,int num){
        String dataStr = String.valueOf(data);
        int index = dataStr.indexOf(".");
        if(index == -1){
            return true;
        }
        int numofDig = dataStr.length() - index;
        return numofDig <= 6;
    }

    /**
     * 方法2，易于理解，精确度高
     * @param a
     * @return
     */
    public static Double squareRoot(int a){
        double x = 0;
        double low = 0;
        double high = a;
        while(low<=high){
            x = (low+high)/2;
            if(x>a/x){
                high = x-0.000001;
            }
            //防止溢出
            if(x<a/x){
                low = x+0.000001;
            }
            if(x==a/x){
                //刚好整除
                return x+0.000001;
            }
        }
        //精确到六位小数
        return new BigDecimal(x).setScale(6, BigDecimal.ROUND_HALF_UP).doubleValue();
    }
    public static void main(String[] args) {
        System.out.println( SqrtUtil.squareRoot(5));
    }
}

　　

八、为什么二分法使用数组作为数据结构，链表可以吗？

• 二分查找 数组查询时间复杂度 O(logn)。

• 假设链表长度为n，二分查找每次都要找到中间点(计算中忽略奇偶数差异):
  第一次查找中间点，需要移动指针n/2次；
  第二次，需要移动指针n/4次；
  第三次需要移动指针n/8次；
  ......
  以此类推，一直到1次为值

• 总共指针移动次数(查找次数) = n/2 + n/4 + n/8 + ...+ 1，这显然是个等比数列，根据等比数列求和公式：Sum = n - 1.

• 最后算法时间复杂度是：O(n-1)，忽略常数，记为O(n)，时间复杂度和顺序查找时间复杂度相同

• 但是稍微思考下，在二分查找的时候，由于要进行多余的运算，严格来说，会比顺序查找时间慢

九、一个循环有序数组，比如 4，5，6，1，2，3，如何实现一个求“值等于给定值”的二分查找算法呢？

class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length-1;
        int mid = left + (right-left)/2;
        while(left <= right){
            if(nums[mid] == target){
                return mid;
            }
            if(nums[left] <= nums[mid]){  //左边升序
                if(target >= nums[left] && target <= nums[mid]){//在左边范围内
                    right = mid-1;
                }else{//只能从右边找
                    left = mid+1;
                }
            }else{ //右边升序
                if(target >= nums[mid] && target <= nums[right]){//在右边范围内
                    left = mid +1;
                }else{//只能从左边找
                    right = mid-1;
                }
            }
            mid = left + (right-left)/2;
        }
        return -1;  //没找到
    }
}

　　

参考文献：

　　https://www.cnblogs.com/hezhiyao/p/7544593.html

　　https://time.geekbang.org/column/article/42520

　　https://www.jianshu.com/p/4d0f476af2b7