1、协作型过滤（collaborative filtering）
一个协作型过滤算法通常的做法是对一大群人进行搜索，并从中找出与我们品味相近的一小群人。算法会对这些人所偏爱的其他内容进行考查，并将它们组合起来构造出一个经过排序的推荐列表。
2、搜索偏好
第一件事情，寻找一种表达不同人及其偏好的方法，使用嵌套字典。
# A dictionary of movie critics and their ratings of a small # set of movies #一个涉及影评者以及对几部影片评分情况的字典 critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5, 'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5, 'The Night Listener': 3.0}, 'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5, 'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0, 'You, Me and Dupree': 3.5}, 'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0, 'Superman Returns': 3.5, 'The Night Listener': 4.0}, 'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0, 'The Night Listener': 4.5, 'Superman Returns': 4.0, 'You, Me and Dupree': 2.5}, 'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0, 'You, Me and Dupree': 2.0}, 'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5}, 'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,'Superman Returns':4.0}}
保存在recommandations.py文件中。上述字典使用从1到5的评分，以此来体现每位影评者对某一给定影片的喜爱程度。
例子：
In [1]: from recommandations import critics In [2]: critics['Lisa Rose']['Lady in the Water'] Out[2]: 2.5 In [3]: critics['Lisa Rose']['Snakes on a Plane'] Out[3]: 3.5 In [4]: critics['Lisa Rose']['Snakes on a Plane'] = 4.5 In [5]: critics['Lisa Rose']['Snakes on a Plane'] Out[5]: 4.5
可以将相当数量的人员偏好信息置于字典内（即内存中），但对于一个规模巨大的数据集而言，更希望将其存入数据库中。
3、寻找相近的用户
将每个人与所有其他人进行对比，并计算他们的相似度评价值。将介绍两套计算相似度评价值的体系：欧几里得距离和皮尔逊相关度。
欧几里德距离评价
以经过人们一致评价的物品为坐标轴，然后将参与评价的人绘制到图上，并考查他们彼此间的距离远近，如图所示：
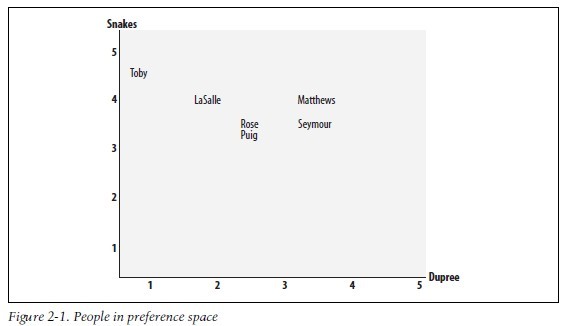
这里有个问题，没搞懂这个图是怎么生成的，先放在这里，等读完这章的时候再来更新。
解释：
def get_score_by_movie(prefs,movie1,movie2): for item in prefs: movie_list = prefs[item] if ( movie1 in movie_list ) and (movie2 in movie_list): name_list = item.split() if len(name_list) > 1: name = name_list[1] else: name = name_list[0] print "%s=(%0.2f,%0.2f)" % (name,critics[item][movie1],critics[item][movie2]) get_score_by_movie(critics,'You, Me and Dupree'，'Snakes on a Plane')
输出：
Matthews=(3.50,4.00) LaSalle=(2.00,4.00) Puig=(2.50,3.50) Rose=(2.50,3.50) Toby=(1.00,4.50) Seymour=(3.50,3.50)
对应的matplotlib代码：
from math import sqrt import matplotlib.pyplot as plt def get_score_by_movie(prefs,movie1,movie2): fig = plt.figure() fig.suptitle('Preference Movie', fontsize=14, fontweight='bold') ax = fig.add_subplot(111) fig.subplots_adjust(top=0.85) ax.set_xlabel(movie1) ax.set_ylabel(movie2) for item in prefs: movie_list = prefs[item] if ( movie1 in movie_list ) and (movie2 in movie_list): name_list = item.split() if len(name_list) > 1: name = name_list[1] else: name = name_list[0] x = critics[item][movie1] y = critics[item][movie2] ax.text(x,y,name) print "%s=(%0.2f,%0.2f)" % (name,x,y)
#起到关键作用，调整坐标轴size，默认为[0,1] ax.axis([0, 5, 0, 5]) plt.savefig("test.png")
输出的结果:
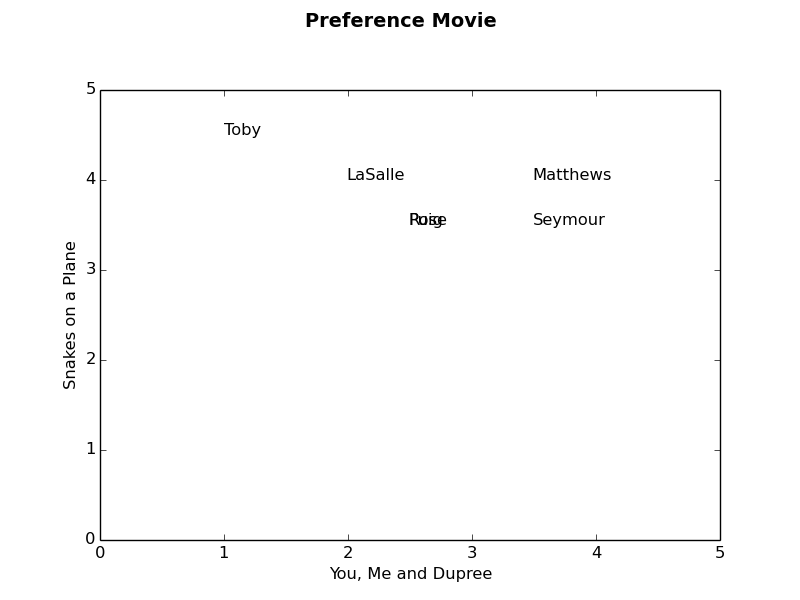
不做ax.axis([0, 5, 0, 5]) ，输出结果如下：
欧几里德距离定义
欧几里得度量定义欧几里得空间中，点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的距离为
向量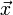 
的自然长度，即该点到原点的距离为
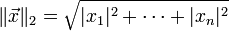
它是一个纯数值。在欧几里得度量下，两点之间直线最短。
代码：
from math import sqrt def sim_distance(prefs,person1,person2): si = {} for item in prefs[person1]: if item in prefs[person2]: si[item] = 1 if len(si) == 0 :return 0
//对同一部电影的喜好程度，构成上面 x = (x1,...,xn) 和 y = (y1,...,yn) sum_of_squares = sum(pow( prefs[person1][item] - prefs[person2][item] , 2) for item in si) return 1/(1+sum_of_squares) if __name__ == '__main__': print sim_distance(critics,'Lisa Rose','Gene Seymour')
输出结果为： 0.148148148148
皮尔逊相关度评价
它在数据不是很normalized的时候（影评者对影片的评价总是相对于平均水平偏离很大时），会倾向给出更好的结果。
如下图Mick LaSalle为Superman评了3分，而Gene Seymour则评了5分，故该影片对应的定位为（3,5）：
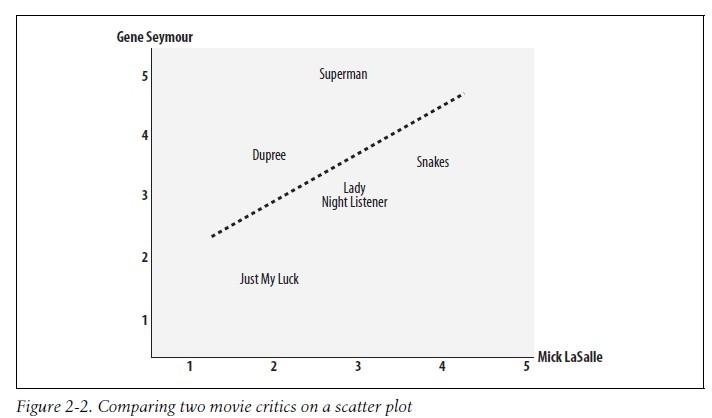
在图上，还可以看到一条直线，其可能地靠近图上的所有坐标，被称作为最佳拟合线。
如果两位评论者对所有影片的评分情况都相同的话，那么这条直线将成为对角线，并且会与图上所有的坐标点都相交，从而得一个结果为1的理想相关度评价。
上图相关系数为0.4左右。下图相关系数为0.75：
在采用皮尔逊方法进行评价时，可以从图上发现一个值得注意的地方，就是它修正“夸大分值”的情况。虽然Jack总是倾向于给出比Lisa更高的分值，但最终的直线仍然是拟合的，这说明他们之间有很好的相关性。
对比欧几里得：
1、皮尔逊：如果某人总是倾向于给出比另一个人更高的分值，而二者的分值之差又始终保持一致，则他们依然可能存在很好的相关性
2、欧几里得：一个人的评价始终比另一个人的更好，从而导致评价始终相对偏低，得出两者不相近的结果。尽管他们的品味很相似也是如此。
假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：
皮尔逊相关度评价算法首先会找出两位评论者都曾评价过的物品，然后计算两者的评分总和与平方和，并求得评分的乘积之和。最后，算法利用这些计算结果计算出皮尔逊相关系数。
http://blog.csdn.net/wsywl/article/details/5727327
代码：
def sim_person(prefs,p1,p2): si = {} for item in prefs[p1]: if item in prefs[p2]: si[item] = 1 n = len(si) if n == 0:return 0 sum1 = sum([prefs[p1][it] for it in si]) sum2 = sum([prefs[p2][it] for it in si]) sum1Sq = sum([pow(prefs[p1][it],2) for it in si]) sum2Sq = sum([pow(prefs[p2][it],2) for it in si]) pSum = sum([prefs[p1][it]*prefs[p2][it] for it in si]) num = pSum - sum1*sum2/n den = sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n)) if den == 0: return 0 return num/den
输出结果为:0.396059017191
该函数将返回介于-1与1之间的数值，值1表明两个人有一致的评价。
应该选用哪一种相似性度量方法
根据实际效果进行选择，皮尔逊、欧几里得距离等任何其他方法。
Jaccard系数或曼哈顿距离算法，作为相似度计算函数，只要满足如下条件：拥有同样的函数签名，以一个浮点数作为返回值，其数值越大代表相似度越大。
为评论者打分
使用上面的相似度计算函数，为影评者打分
def topMatches(prefs,person,n=5 ,similarity=sim_person): scores = [(similarity(prefs,person,other),other) for other in prefs if other!=person] scores.sort() scores.reverse() print scores return scores[0:n] topMatches(critics,'Lisa Rose')
[(0.9912407071619299, u'Toby'), (0.7470178808339965, u'Jack Matthews'), (0.5940885257860044, u'Mick LaSalle'), (0.5669467095138396, u'Claudia Puig'), (0.40451991747794525, u'Michael Phillips'), (0.39605901719066977, u'Gene Seymour')]
（待续）