二叉树的重建问题
作者:Grey
原文地址:
说明
二叉树的各种遍历见二叉树的先,中,后序遍历(递归,非递归,Morris方法)
根据中序遍历和后序遍历重建二叉树
链接地址:LeetCode 106. Construct Binary Tree from Inorder and Postorder Traversal
特别注意,本题的约束条件中,一定要保证inorder 和 postorder 都由不同的值组成。由于
中序遍历的顺序是:左 -> 中 -> 右
后序遍历的顺序是:左 -> 右 -> 中
所以对一棵树,其中序遍历的样子如下

后序遍历的样子如下

定义递归函数
TreeNode f(中序遍历结果, int L1, int R1, 后序遍历结果, int L2, int R2)
递归含义表示:中序遍历的L1...R1和后序遍历L2...R2构造出的二叉树,返回根节点。
所以主函数调用
f(inorder, 0, L, postorder, 0, L);
即为答案。
接下来实现这个递归函数,由于后序遍历的最后一个节点就是树的根节点,所以

// 树的根节点
树的根节点 = new TreeNode(后序遍历最后一个节点);
树的根节点在中序遍历的节点位置假设在如下 index 位置
那么在中序遍历中,左树为[L1......index - 1]。

中序遍历的剩下部分用来构造右树:[index + 1, R1],
在后序遍历中,左树为[L2......L2 + index - L1 - 1]
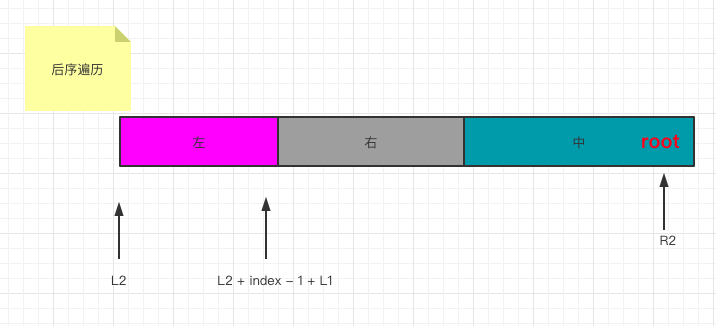
后序遍历的剩下部分用来构造右树:[L2 + index - L1, R2 - 1]
由于要记录某个节点在中序遍历中的位置,所以需要准备一个哈希表,用于存某个元素在中序遍历的位置。
int L = inorder.length - 1;
Map<Integer, Integer> m = new HashMap<>();
for (int i = 0; i <= L; i++) {
m.put(inorder[i], i);
}
完整代码如下
class Solution {
public static TreeNode buildTree(int[] inorder, int[] postorder) {
if (null == postorder || inorder == null || postorder.length != inorder.length) {
return null;
}
int L = inorder.length - 1;
Map<Integer, Integer> m = new HashMap<>();
for (int i = 0; i <= L; i++) {
m.put(inorder[i], i);
}
return f(inorder, 0, L, postorder, 0, L, m);
}
private static TreeNode f(int[] inorder, int L1, int R1, int[] postorder, int L2, int R2, Map<Integer, Integer> m) {
// 这种
if (L2 > R2) {
return null;
}
TreeNode root = new TreeNode(postorder[R2]);
// 如果只有一个节点,则直接返回
if (L2 == R2) {
return root;
}
int index = m.get(postorder[R2]);
root.left = f(inorder, L1, index - 1, postorder, L2, L2 + index - L1 - 1, m);
root.right = f(inorder, index + 1, R1, postorder, L2 + index - L1, R2 - 1, m);
return root;
}
}
根据先序遍历和中序遍历重建二叉树
链接地址:LeetCode 105. Construct Binary Tree from Preorder and Inorder Traversal
对于一棵树,中序遍历的样子如下

先序遍历的样子如下

而且,先序遍历的第一个节点,就是根节点,然后定位根节点在中序遍历的位置,假设在 index 位置,则
中序遍历中,左树为[L2.......index - 1],剩余部分[index + 1.......R2]去构造右树。
先序遍历中,左树为[L1 + 1......index - L2 + L1],剩余部分[index - L2 + L1 + 1......R1]去构造右树。
完整代码如下
class Solution {
public static TreeNode buildTree(int[] preorder, int[] inorder) {
if (null == preorder || inorder == null || preorder.length != inorder.length) {
return null;
}
int L = inorder.length - 1;
Map<Integer, Integer> m = new HashMap<>();
for (int i = 0; i <= L; i++) {
m.put(inorder[i], i);
}
return f(preorder, 0, L, inorder, 0, L, m);
}
private static TreeNode f(int[] preorder, int L1, int R1, int[] inorder, int L2, int R2, Map<Integer, Integer> m) {
if (L1 > R1) {
return null;
}
TreeNode root = new TreeNode(preorder[L1]);
if (L1 == R1) {
return root;
}
int index = m.get(preorder[L1]);
root.left = f(preorder, L1 + 1, index - L2 + L1, inorder, L2, index - 1, m);
root.right = f(preorder, index - L2 + L1 + 1, R1, inorder, index + 1, R2, m);
return root;
}
}