作者:Grey
原文地址:使用并查集处理集合的合并和查询问题
要解决的问题
有若干个样本a、b、c、d…,假设类型都是V,在并查集中一开始认为每个样本都在单独的集合里,用户可以在任何时候调用如下两个方法 :
方法1:查询样本x和样本y是否属于一个集合,即:
boolean isSameSet(V x,V y);
方法2:把x和y各自所在集合的所有样本合并成一个集合,即:
void union(V x, V y)
但是,isSameSet和union方法的代价越低越好,在这两个方法调用非常频繁的情况下,这两个方法最好能做到O(1)的时间复杂度。
数据结构设计
节点类型定义如下:
private static class Node<V> {
private final V value;
public Node(V value) {
this.value = value;
}
}
但是每个节点都有一条往上指的指针,节点a往上找到的头节点,叫做a所在集合的代表节点,查询x和y是否属于同一个集合,就是看看找到的代表节点是不是一个,如果代表节点是同一个,说明这两个节点就是在同一集合中,把x和y各自所在集合的所有点合并成一个集合,只需要某个集合的代表点挂在另外一个集合的代表点的下方即可。
我们可以使用三张哈希表:
// 快速找到某个节点是否存在
private HashMap<V, Node<V>> nodeMap;
// 找到某个节点的父节点
private HashMap<Node<V>, Node<V>> parentMap;
// 每个代表节点代表的节点个数
private HashMap<Node<V>, Integer> sizeMap;
其中的parentMap就充当了找代表节点的责任,查询任何一个节点x的代表节点,只需要调用如下方法即可:
parentMap.get(x)
现在以一个实际例子来说明并查集的基本操作,假设现在有如下的样本,现在每个样本都是独立的集合,每个样本各自都是自己的代表节点,
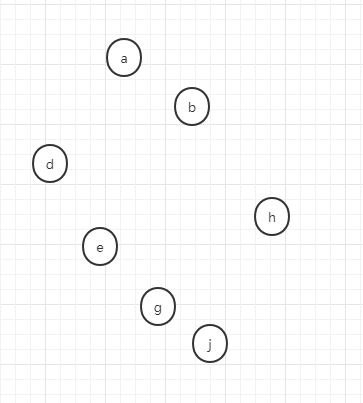
假设我做如下操作,
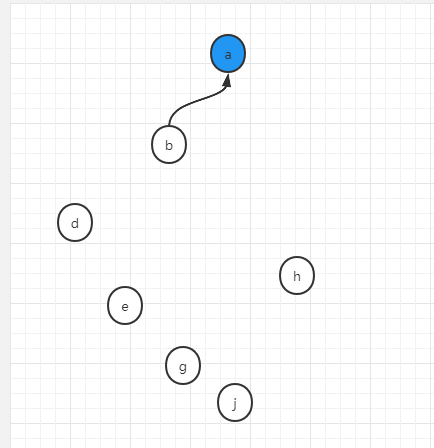
第一个操作,将a和b合并成一个集合
union(a,b)
操作完毕后,a和b将做如下合并操作,合并后,先随便以一个点作为合并集合的代表节点,假设代表节点用蓝色表示
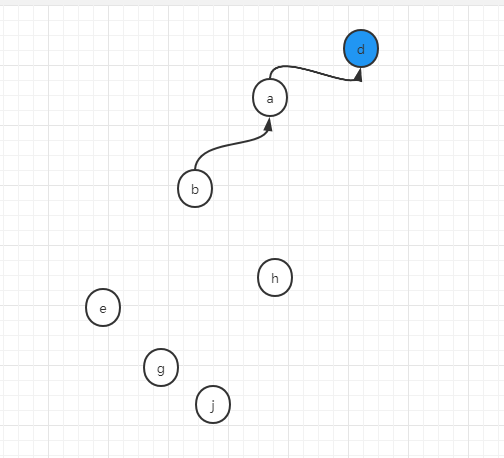
第二个操作,将b和d合并成一个集合
union(b,d)
此时,b将找到其代表节点a,d将找到其代表节点也就是它本身d,将d和a合并在一起,假设我们用a去连d,然后将a,b,d这个集合的代表节点更新为d
即:
第三个操作,将b和h合并成一个集合
union(b,h)
此时,b将找到其代表节点d,h将找到其代表节点也就是它本身h,将d和h合并在一起,假设我们用d去连h,然后将a,b,d,h这个集合的代表节点更新为h,如下图
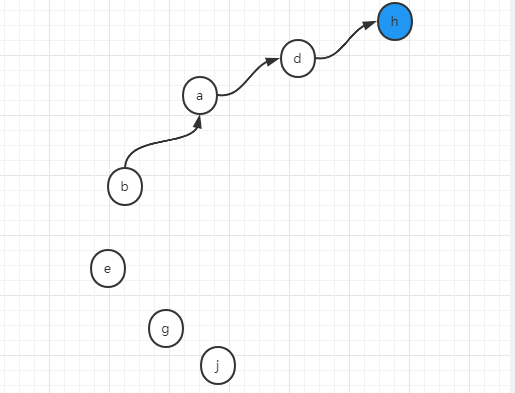
假设e,g,j都做同样的合并
union(e,g)
union(g,j)
结果如下
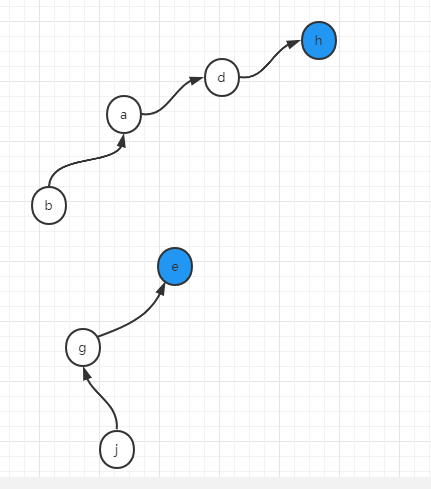
最后,假设我们调用
union(j,b)
即:将j所在集合和b所在集合合并在一起,那么就需要j一直向上找到其代表节点e,b向上找到其代表节点h,然后将两个代表节点连接起来即可,比如可以是这样
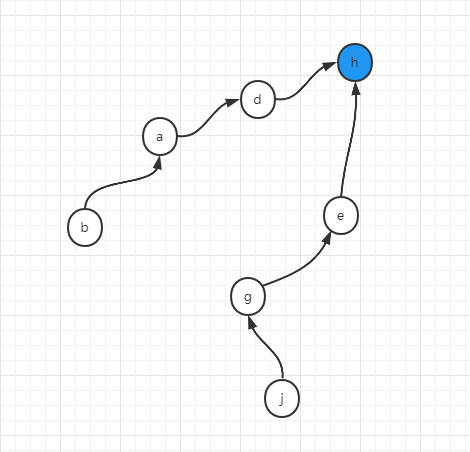
并查集的优化
根据如上流程示例,我们可以了解到一个问题,就是如果两个节点距离各自的代表节点比较长,比如上面的b点距离其代表节点h就比较长,随着数据量增多,这会极大影响效率,所以,并查集的第一个优化就是:
节点往上找代表点的过程,把沿途的链变成扁平的
举例说明,我们上述例子中的第二个操作,将b和d合并成一个集合
union(b,d)
此时,b将找到其代表节点a,d将找到其代表节点也就是它本身d,将d和a合并在一起,假设我们用a去连d,然后将a,b,d这个集合的代表节点更新为d
即:

如果做了扁平化操作,那么在合并b和d的过程中,不是简单的用a去连d,而是将a节点的所有下属节点都直连d,所以就变成了:
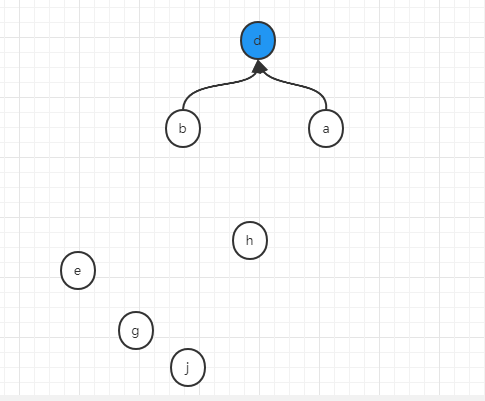
如果我们每一次做union操作,都顺便做一次扁平化,那么上述例子在最后一步执行之前,应该是这样的状态
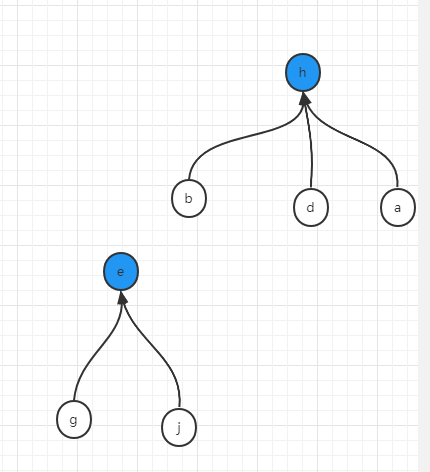
如果变成了这样的状态,那么每次找自己的代表节点这个操作,只需要往上看一次就可以。这在具体代码实现上使用了队列,即,将某个节点往上直到代表节点的所有元素都记录在队列里面,然后将记录在队列中的所有元素的父节点都指向代表节点。
private Node<V> findFather(Node<V> node) {
// 沿途节点都放队列里面
// 然后将队列元素做扁平化操作
Queue<Node<V>> queue = new LinkedList<>();
while (node != parentMap.get(node)) {
queue.offer(node);
node = parentMap.get(node);
}
while (!queue.isEmpty()) {
// 优化2:扁平化操作
parentMap.put(queue.poll(), node);
}
return node;
}
并查集的第二个优化是:
小集合挂在大集合的下面
举例说明,假设我们经过了若干次的union之后,形成了如下两个集合,显然,h为代表节点的集合是小集合,只有四个元素,而以e为代表节点的集合是相对来说就是大集合。
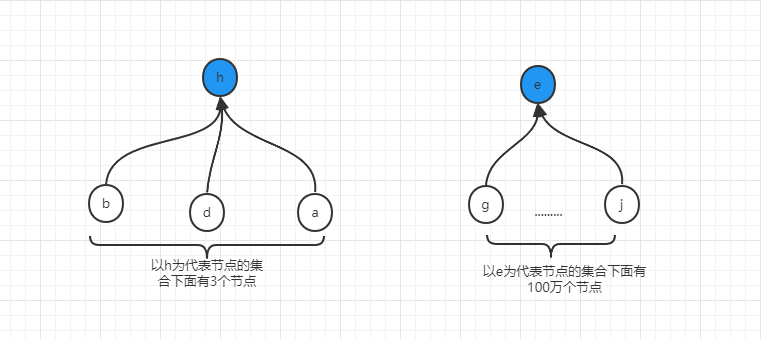
如果此时,要合并b节点所在集合(代表节点为h)和j几点所在集合(代表节点为e),那么就面临到底应该迁移e及其下面所有的点到h上,还是应该迁移h及下面所有的点到e上,从两个集合的数量上来说,迁移h集合到e上的代价要比迁移e到h上的代价要低的多,所以这就是并查集的第二个优化。
经过了如上两个优化,并查集中的union或者isSameSet方法如果调用很频繁,那么单次调用的代价为O(1),两个方法都如此。
完整代码
package snippet;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class Code_0049_UnionFind {
public static class UnionFind<V> {
// 快速找到某个节点是否存在
private HashMap<V, Node<V>> nodeMap;
// 找到某个节点的父节点
private HashMap<Node<V>, Node<V>> parentMap;
// 每个代表节点代表的节点个数
private HashMap<Node<V>, Integer> sizeMap;
public UnionFind(List<V> values) {
nodeMap = new HashMap<>();
parentMap = new HashMap<>();
sizeMap = new HashMap<>();
for (V v : values) {
Node<V> n = new Node<>(v);
nodeMap.put(v, n);
parentMap.put(n, n);
sizeMap.put(n, 1);
}
}
// v1,v2必须是已经存在nodeMap中的元素
public void union(V v1, V v2) {
if (!nodeMap.containsKey(v1) || !nodeMap.containsKey(v2)) {
return;
}
if (!isSameSet(v1, v2)) {
Node<V> v1Parent = nodeMap.get(v1);
Node<V> v2Parent = nodeMap.get(v2);
Node<V> small = sizeMap.get(v1Parent) > sizeMap.get(v2Parent) ? v2Parent : v1Parent;
Node<V> large = small == v1Parent ? v2Parent : v1Parent;
sizeMap.put(large, sizeMap.get(large) + sizeMap.get(small));
// 优化1:小集合挂在大集合下面
parentMap.put(small, large);
parentMap.remove(small);
}
}
private Node<V> findFather(Node<V> node) {
Queue<Node<V>> queue = new LinkedList<>();
while (node != parentMap.get(node)) {
queue.offer(node);
node = parentMap.get(node);
}
while (!queue.isEmpty()) {
// 优化2:扁平化操作
parentMap.put(queue.poll(), node);
}
return node;
}
public boolean isSameSet(V v1, V v2) {
if (!nodeMap.containsKey(v1) || !nodeMap.containsKey(v2)) {
return false;
}
return findFather(nodeMap.get(v1)) == findFather(nodeMap.get(v2));
}
private static class Node<V> {
private final V value;
public Node(V value) {
this.value = value;
}
}
}
}