树链剖分
http://www.lydsy.com/JudgeOnline/problem.php?id=1036
https://oi.men.ci/tree-chain-split-notes/、
点分治
https://oi.men.ci/tree-divide-notes/
https://www.luogu.org/blog/chengni5673/dian-fen-zhi
对于一棵树,统计长度为 x 的路径的路径数.
点分治: 找到一个点为根,统计答案,然后将它的子树分离,分别进行同样的操作,继续,直到只剩下一个点. 其中选择的根是有要求的,为了保证时间复杂度,我们需要尽量的让子树的大小相近,所以每一次我们选择的根都最好是当前这棵树的重心.
图论常见技巧
- 反向建边
- 虚点连边
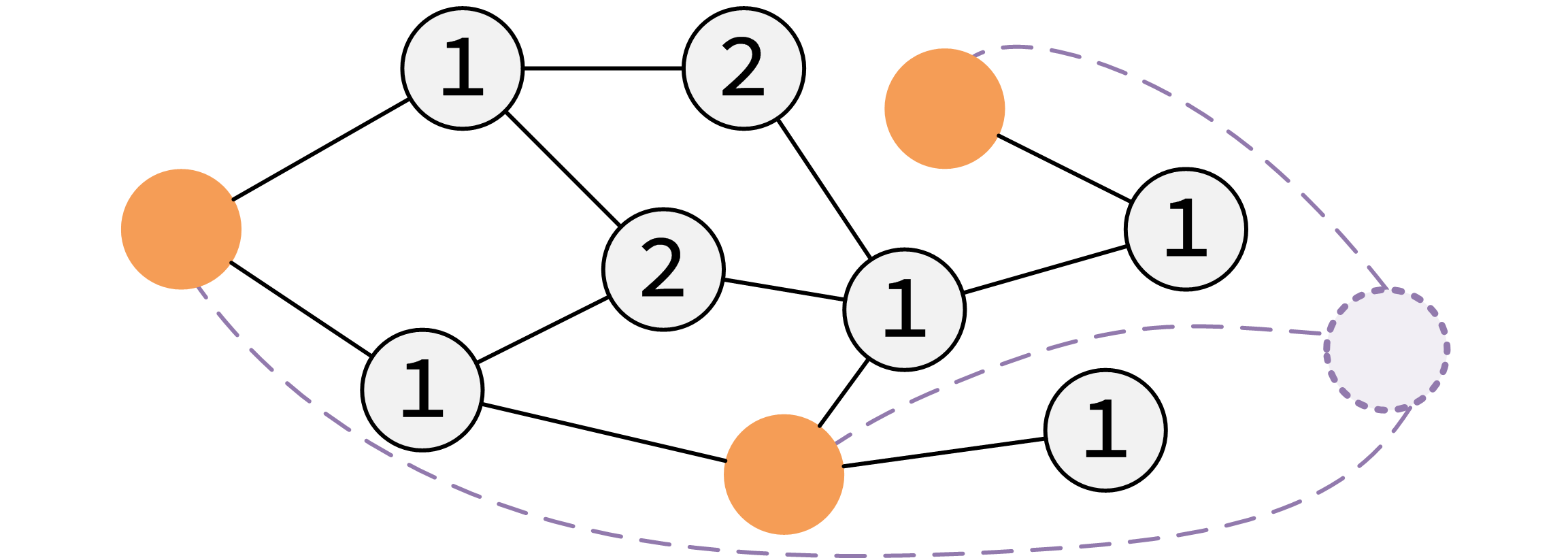
Graph 1. 求各点到指定点集的最短距离的优化方法
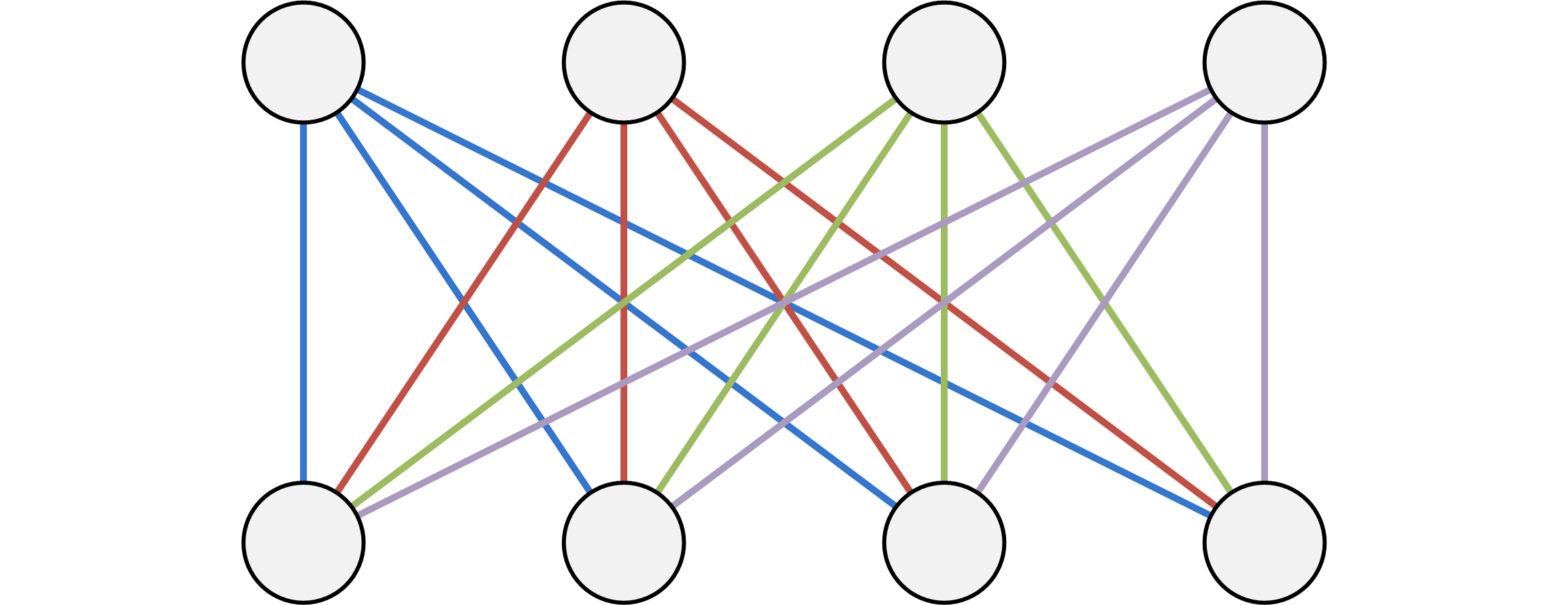
(a)
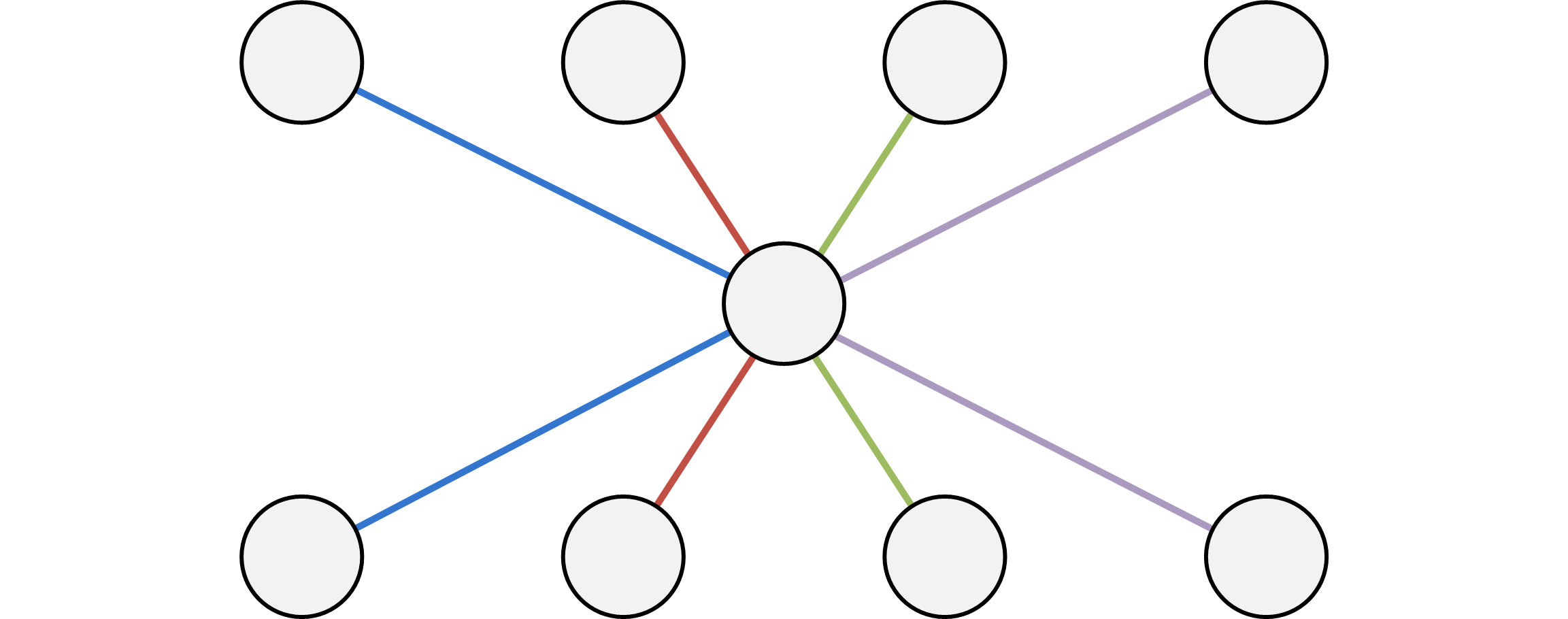(b)
Graph 2. 二分完全图建边的优化方法
- 建边的线段树优化
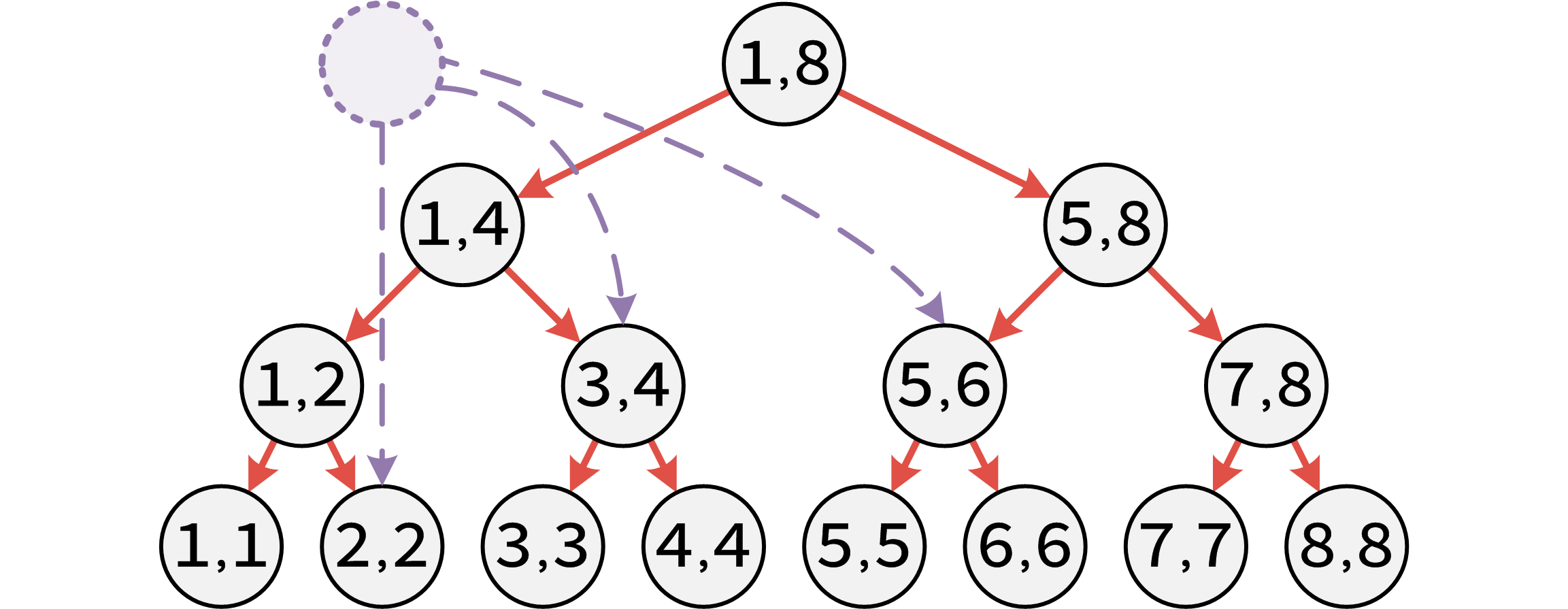
Graph 3. 建边的线段树优化
- 拆点
- 分层图解决刁钻图上操作
分层图就是有多维状态的有边长图,比起正常的最短路转移多了一种跨维度转移的状态转移. 一般都是舍去某边长度,最多舍多少次 (次数较少).
[JLOI2011] 飞行路线: Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 n 个城市设有业务,设这些城市分别标记为 0 到 n-1,一共有 m 种航线,每种航线连接两个城市,并且航线有一定的价格。Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 k 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
分层图可以很巧妙的解决这个问题. 想象你每次使用免费航线之前和之后分别存在于不同的时空 (不同的层) 里面,每使用一次免费航线,你就从这个时空进入了另一个时空 (免费). 根据以上思想建图,一共建 k+1 层图,相邻的两层图中进行连边 (单向边,距离为 1). 然后跑 Dijkstra 即可.
图论的注意点
- 无向图/有向图
- 自环、重边
- 环(缩点)
- 负环、零环