2020-2021年度第二届全国大学生算法设计与编程挑战赛(冬季赛)——热身赛 D题
题意:
给出一个图,分山顶山谷,只有山顶和山谷之间连边,显然得图为二分图。
从左侧点出发,轮流走,直到不能走,停在顶则Cong胜,反之则Ni胜,自然可想到博弈论方向。
分析:
我们对其跑一个最大匹配,其增广路径为匹配边,非匹配边交替。
- 若一条连续增广路径如图,左侧点数大于右侧点数,则无论如何,从左侧出发,最后必然会落在左侧。
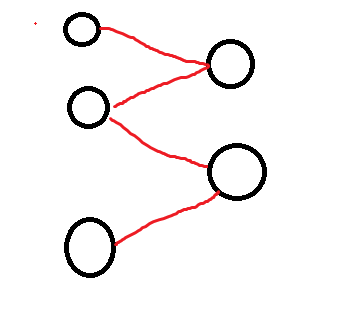
- 若一条连续最长增广路径如图,左侧点数小于等于右侧点数,则无论如何,从左侧出发,最后必然落在右侧。
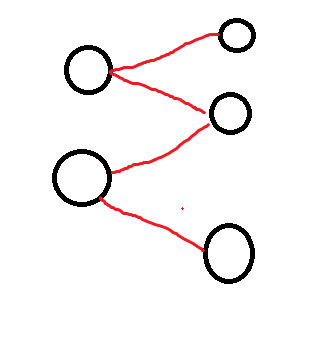
我们建立超级源点s和超级汇点t,对该二分图跑一个最大流。
对于偶数个边,必然在增广路径两头有一个左侧的点没有流量,所以我们从超级源点按照容量余下1的边遍历(从右向左为反边的流量容量),所有遍历到的左侧点为败点。
对于奇数个边,则增广路径中的左侧点必然都有流量,所以我们从超级源点遍历时遍历不到,故未被遍历到的点都为胜点。
结论
我们对原二分图用超级源汇跑一个最大流,在从源点bfs所有流量容量为1的边。所有被标记的左点都为Cong赢,没有被标记的左点都为Ni赢。
/***********************************
dinic最大流思路:
不断图分层,保证dfs过程中,不会出现环等现象
在一次分层中,用dfs一次性搜寻多条增广路。
就是向下搜,搜到t为止,然后返回流量。
当前节点最大流量为的下属分支所有流量的返回最大流量。
下属分支返回的流量为min(通往该分支边的最大流量,分支的下属总流量)
当dfs一次后,一定会有某些边被榨干,改变分层图。
再次分层图,重复上述过程。
分层图用bfs实现。如果bfs不到终点,则结束算法。
************************************/
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<queue>
using namespace std;
typedef long long ll;
typedef long long ii;
const ll maxn = 1e5 + 50;
const ll maxm = 1e5 + 50;
const ll INF = ll(1) << 50;
struct e {
ll next, to, flow;
} edge[maxm * 2];
int head[maxn * 2], tot = 0;
void add(ll u, ll v, ll flow) {
edge[tot].to = v; edge[tot].next = head[u];
edge[tot].flow = flow; head[u] = tot++;
edge[tot].to = u; edge[tot].next = head[v];
edge[tot].flow = 0; head[v] = tot++;
}
ll n, m, s, t;
ll dis[maxn * 2];
queue<ll> q;
ll cur[maxn * 2];
ll dfs(ll u, ll lim) {
if (u == t)return lim;
ll flow = 0;
for (ll i = cur[u]; ~i; i = edge[i].next) {
cur[u] = i;
ll v = edge[i].to;
if (dis[v] != dis[u] + 1 || edge[i].flow == 0) {
continue;
}
ll f = dfs(v, min(edge[i].flow, lim));
flow += f; lim -= f;
edge[i].flow -= f; edge[i ^ 1].flow += f;
if (lim == 0)break;
}
return flow;
}
ll bfs() {
while (!q.empty())q.pop();
for (ll i = 0; i <= n * 2 + 1 ; i++) {
dis[i] = INF;
cur[i] = head[i];
}
dis[s] = 0;
q.push(s);
while (!q.empty()) {
ll u = q.front(); q.pop();
for (ll i = head[u]; ~i; i = edge[i].next) {
ll v = edge[i].to;
if (edge[i].flow == 0 || dis[v] != INF)continue;
dis[v] = dis[u] + 1;
q.push(v);
}
}
if (dis[t] == INF)return 0;
else return 1;
}
void dfs4(int u, int p) {
}
void init() {
for (ll i = 0; i <= n * 2 + 50; i++) {
head[i] = -1;
}
}
int check[maxn * 2];
void bfs2() {
queue<int> q;
q.push(s);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = head[u]; ~i; i = edge[i].next) {
int v = edge[i].to;
if (edge[i].flow == 1 && check[v] != 1 ) {
q.push(v);
check[v] = 1;
}
}
}
}
int main() {
scanf("%lld%lld", &n, &m);
init();
s = 0; t = 2 * n + 1;
ll a, b;
for (int i = 1; i <= n; i++) {
add(s, i, 1);
add(i + n, t, 1);
}
for (int i = 0; i < m; i++) {
scanf("%lld%lld", &a, &b);
add(a, b + n, 1);
//add(b + n, a, 1);
}
ll maxflow = 0;
while (bfs()) {
maxflow += dfs(s, INF);
}
bfs2();
for (int i = 1; i <= n; i++) {
if (check[i] == 0) {
puts("Ni");
} else {
puts("Cong");
}
}
return 0;
}