动态规划--多重背包

题目：https://www.acwing.com/problem/content/4/

多重背包题意同完全背包，不过多了一个限制，就是每种物品有数目限制。

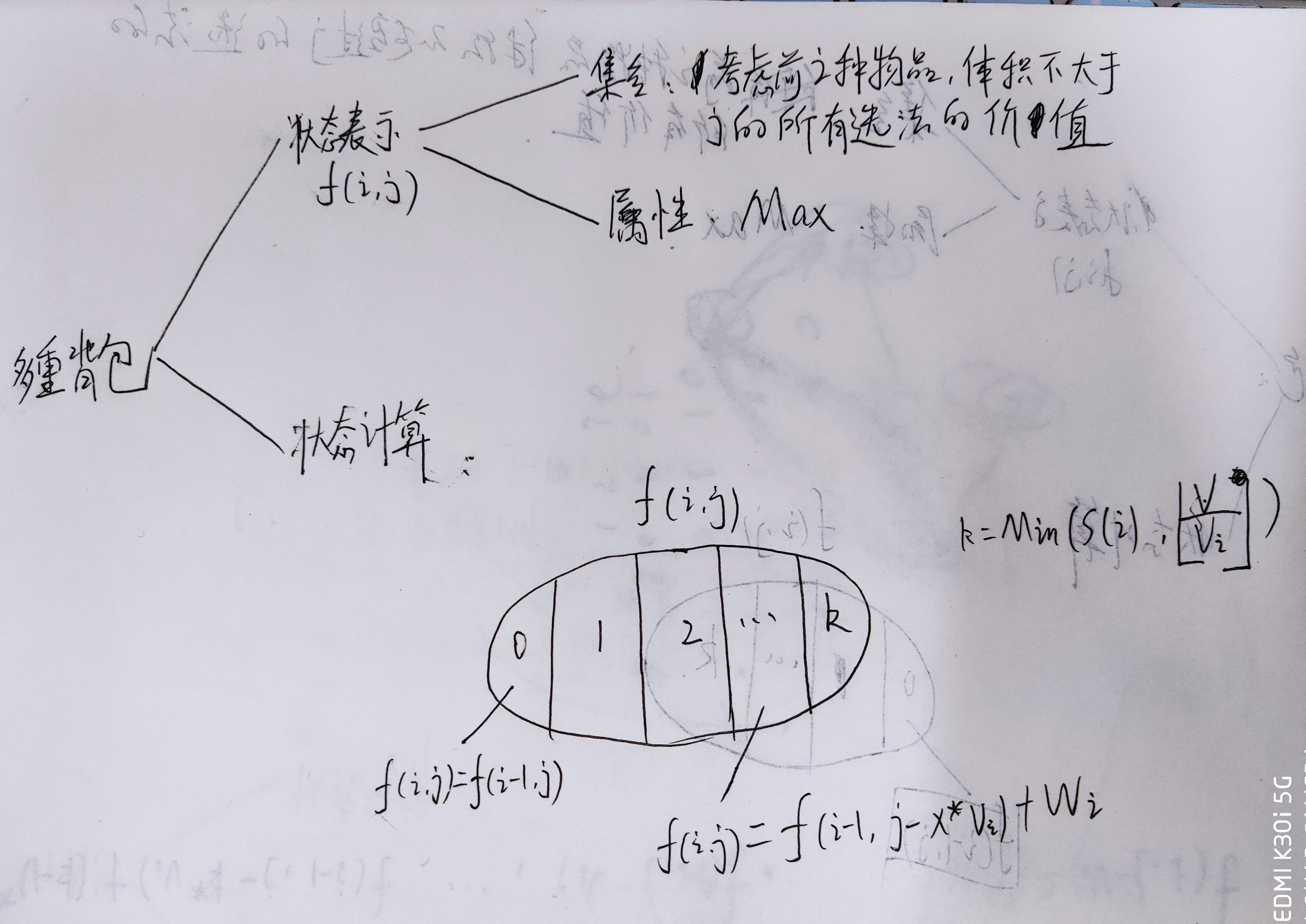
朴素想法

最朴素的想法就是直接枚举每种物品拿多少个。

#include<iostream>
using namespace std;
const int N=110;
int v[N],w[N],s[N];
int f[N][N];
int main(void){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>v[i]>>w[i]>>s[i];
    }
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];
            for(int k=1;k<=s[i]&&j>=k*v[i];k++){
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[n][m];
    return 0;
}

但是这样做的时间复杂度为n*m*s，时间代价过高。

二进制优化

我们如果可以用更少的数将 s [ i  ] 代替的话，同时保持答案的准确性的话，时间就会减少。

需要用到的定理

 用来表示s [ i ] 的数的获取方法

 那么在将s [ i ] 替换之后，只需要把新的物品序列当成01背包来做就OK了。

#include<iostream>
using namespace std;
const int N=12000,M=2100;
int v[N],w[N],cnt;
int f[M];
int main(void){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;
        while(k<=s){
            cnt++;
            v[cnt]=a*k;
            w[cnt]=b*k;
            s-=k;
            k<<=1;
        }
        if(s){
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }
    for(int i=1;i<=cnt;i++){
        for(int j=m;j>=v[i];j--){
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m];
    return 0;
}

单调队列优化

(整不明白)

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20010;
int n,m;
int f[N],g[N],q[N];
int main(void){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        int c,w,s;
        cin>>c>>w>>s;
        memcpy(g,f,sizeof(f));
        
        for(int j=0;j<c;j++){
            int hh=0,tt=-1;
            
            for(int k=j;k<=m;k+=c){
                // f[k]=g[k];
                while(hh<=tt && k-s*c > q[hh]) hh++;//q[hh] < k- s* c代表全部放进去还没有放满，而w恒大于0，所以其他的策略比更优
                if(hh<=tt) f[k]=max(f[k],g[q[hh]] + (k-q[hh]) / c *w );
                while(hh<=tt&&g[q[tt]] - (q[tt]-j) / c * w <= g[k]-(k-j) / c * w) tt--;
                q[++tt]=k;
            }
        }
    }
    cout<<f[m]<<endl;
    return 0;
}