P2024 食物链（种类并查集||带权并查集）

先写所谓的种类并查集。

就是开3*n的空间，前n为A，后边依次是B，C

食物链为A->B->C->A

对于每句话都是先判断是否合法，然后在改并查集就好了

#include<iostream>
#include<fstream>
using namespace std;
const int N=5e4+100;
int fa[N*3];
int finds(int x)//正常的并查集find函数
{
    while(fa[x]!=x)
    {
        x=fa[x];
    }
    return x;
}
int main(void)
{
//    ifstream in("eat.in");
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=3*n;i++)
    {
        fa[i]=i;
    }
    int ans=0;
    for(int i=1;i<=k;i++)
    {
        int d,x,y;
        cin>>d>>x>>y;
        if(x<=0||y<=0||x>n||y>n)//存在不合法的编号就是假话
        {
            ans++;
            continue;
        }
        if(d==1)//这句话说x和y是同类
        {
            if(finds(x+n)==finds(y)||finds(x)==finds(y+n))//如果x吃y或者y吃x
            {
                ans++;
            }
            else//如果是合法的，那么就得把这句话所说的加入到并查集内
            {
                fa[finds(x)]=finds(y);
                fa[finds(x+n)]=finds(y+n);
                fa[finds(x+2*n)]=finds(y+2*n);
            }
        }
        else if(d==2)//这句话说x吃y
        {
            if(finds(x)==finds(y)||finds(x)==finds(y+n))//如果xy同类或者y吃x
            {
                ans++;
            }
            else//如果合法，就得把这句话所说的加入到并查集内
            {
                fa[finds(x+n)]=finds(y);
                fa[finds(x+n+n)]=finds(y+n);
                fa[finds(x)]=finds(y+n+n);
            }
        }
    }
//    ofstream out("eat.out");
    cout<<ans<<endl;
    return 0;
}

 带权并查集有点像dp了，看命。。。

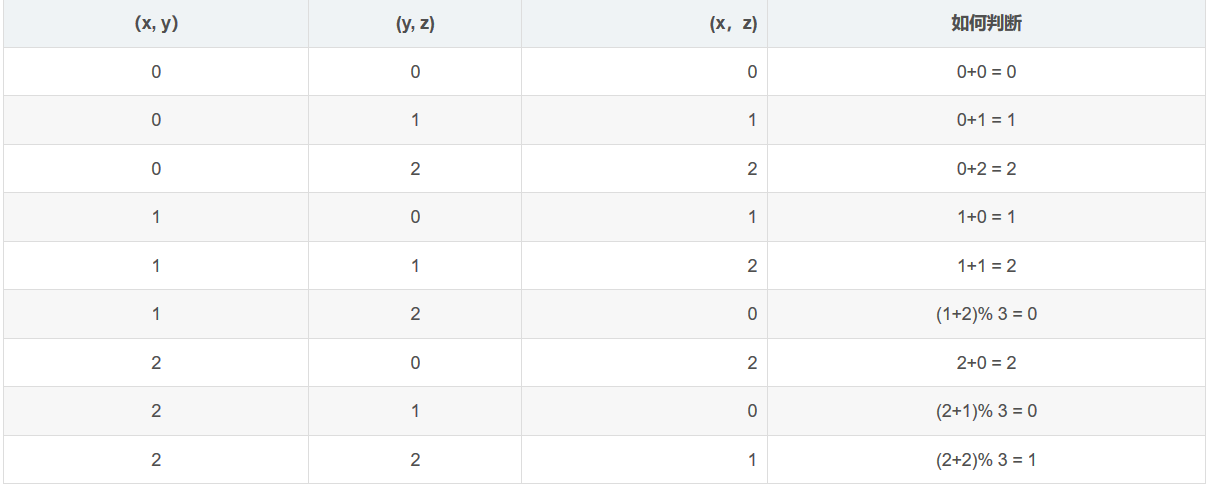
图来自https://blog.csdn.net/u013075699/article/details/80379263

可以得出r[z] = (r[x] + r[y]) % 3;也就是查找（顺便路径压缩的时候的r数组改变方式就有了）

然后再盗一张

这样一来合并的时候的r数组改变也就有了

#include<iostream>
#include<fstream>
using namespace std;
const int N=5e4+100;
int fa[N];
int r[N];//0表示同类，1表示父节点吃子结点，2表示子结点吃父节点
int finds(int x)
{
    while(fa[x]!=fa[fa[x]])//如果父节点还存在父节点，就继续往上
    {
        r[x]=(r[x]+r[fa[x]])%3;//更新关系，可从表中得出
        
        //在这里折磨了好久，不能先改fa[x],而要先改r数组
        
        fa[x]=fa[fa[x]];//越过父节点
    }
    return fa[x];
}//并查集finds函数

void Union(int p,int q,int d)
{
    int pRoot=finds(p);
    int qRoot=finds(q);
    if(pRoot==qRoot)
    {
        return ;
    }
    fa[qRoot]=pRoot;//将第二个集合并入第一个
    //改权值
    r[qRoot]=(r[p]-r[q]+3+(d-1))%3;
}
int main(void)
{
//    ifstream in("eat.in");
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        fa[i]=i;
        r[i]=0;
    }
    int ans=0;
    for(int i=1;i<=k;i++)
    {
        int d,x,y;
        cin>>d>>x>>y;
        if(x<=0||y<=0||x>n||y>n)
        {
            ans++;
            continue;
        }
        if(finds(x)==finds(y))
        {
            if(d==1&&r[x]!=r[y])//说x和y是同类，但其实不是
            {
                ans++;
            }
            if(d==2&&(r[x]+1)%3!=r[y])//说x吃y，但其实x并不吃y
            {
                ans++;
            }
        }
        else
        {
            Union(x,y,d);
        }
    }
    cout<<ans;
//    ofstream out("eat.out");
    return 0;
}