昨天进行了noip的模拟赛,我这个蒟蒻又是垫底....
T1
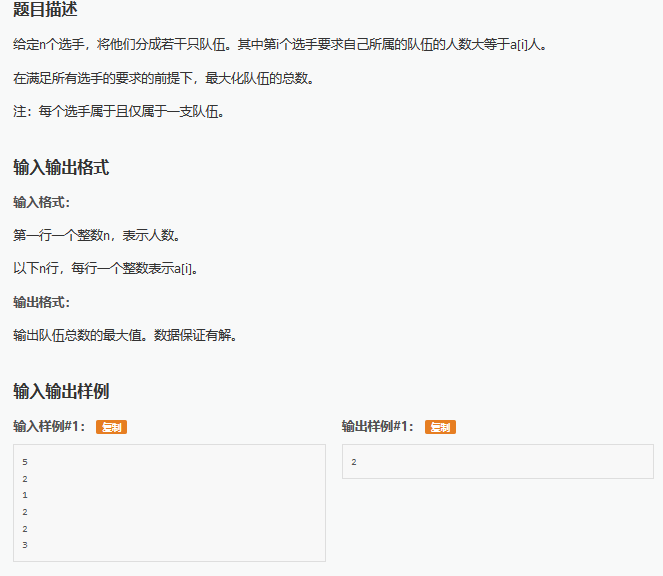
第一感觉就是贪心,从高到低排序,然后每次都将恰好满足当前条件的人数分成一组,然后移动到下一个未分组的单位上,贴代码
#include<bits/stdc++.h>
using namespace std;
const int N=1110000;
int d[N],ans;
bool cmp(int a,int b)
{
return a>b;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&d[i]);
sort(d+1,d+1+n,cmp);
int pos=1;
while(pos!=n+1)
{
ans++;
pos+=d[pos];
}
printf("%d
",ans);
}
只能拿80分,存在反例 4 4 4 4 3 1 1 1 ,贪心的话得到3,最优解是4,所以这样贪心是有问题的,老师说贪心可以过,但我不会写....
正解是dp,从小到大排序,对于每个i,都可以与包括他的前面的d[i]个人分为一组,所以定义dp[i]为满足前i个人条件所能构成队伍数量的最大值,得到转移式:dp[i]=max{dp[j],0<j<=i-d[i]}+1
但这样的话有两层循环,时间复杂度是n的平方,而数据范围为10^6,会超时,所以要优化一下,大概就是保证dp[i] 为dp[1]到dp[i] 的最大值,然后就可以省去枚举j,贴代码
#include<bits/stdc++.h>
using namespace std;
const int N=1110000;
int d[N],dp[N];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&d[i]);
sort(d+1,d+1+n);
for(int i=1;i<=n;i++)
{
if(i>=d[i]) dp[i]=dp[i-d[i]]+1;
dp[i]=max(dp[i],dp[i-1]);
}
printf("%d
",dp[n]);
return 0;
}
T2
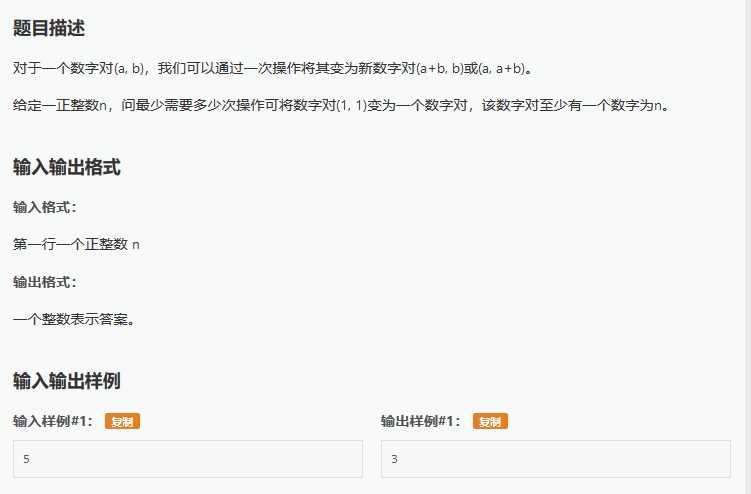
我写的dfs...然后莫名RE...
有同学写的bfs,也非常易懂,不会出现爆栈的危险,但最后几个点超时
#include <bits/stdc++.h>
using namespace std;
int n;
struct node{
int l,r,t;
};
queue <node>q;
int main(){
scanf("%d",&n);
node temp,x1,x2;
temp.l=1;temp.r=1;temp.t=0;
q.push(temp);
while(!q.empty()){
temp=q.front();
q.pop();
if((temp.l+temp.r)==n) {
printf("%d",temp.t+1);
return 0;
}
if((temp.l+temp.r)<n){
x1.l=temp.l+temp.r;x1.r=temp.r;x1.t=temp.t+1;
q.push(x1);
x2.l=temp.l;x2.r=temp.l+temp.r;x2.t=temp.t+1;
q.push(x2);
}
}
return 0;
}
可以发现,对于一个数对(a,b),当a>b时,可由(a-b,b)得到;当a<b时,可由(a,b-a)得到;当a=b时,不可能由(1,1)变换得到;
所以我们可以倒着推,设T(a,b)为从(1,1)变换成(a,b)所需要的次数,在a/b时,有T(a,b)=T(b,a%b)+a/b,所以可以剪枝
答案为min{T(n,i),0<i<=n}
代码
#include<bits/stdc++.h>
using namespace std;
int check(int a,int b)
{
if(b==1)return a-1;
if(!b) return 1e8;
return a/b+check(b,a%b);
}
int main()
{
int n,ans=1e8;
scanf("%d",&n);
for(int i=1;i<=n;i++)
ans=min(check(n,i),ans);
printf("%d
",ans);
return 0;
}
T3

待编辑